Лекция 14. Быстрые схемы дискретного преобразования Фурье.
Обычные формулы для вычисления ДПФ требуют большого количества умножений: 
, где 
- число точек в ДПФ. Существуют приемы, позволяющие уменьшить это количество. Они называются быстрыми схемами (БПФ). Простейшая относится к случаю 
.
Случай
Любое число в интервале 
однозначно представляется двоичным вектором длины 
. Если последовательность 
задана, то положим
. В дальнейшем, что упростить изложение, введем обозначение 
, откуда 
. Имеем
. Основное замечание заключается в следующем: суммирование по индексу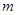 
равносильно суммированию по всем двоичным индексам 
.
, каждый из которых принимает два значения.
Для числа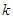 
существует аналогичное двоичное представление: 
. Рассмотрим самую внутреннюю сумму. 
. Нетрудно видеть, что это некоторая функция 
. Следующая сумма принимает вид 
. Этот процесс продолжается. Окончательно имеем 
. Количество сумм равняется 
, в каждой из которых лишь одно умножение. Для вычисления всех коэффициентов нужно 
умножений. Другое преимущество этой схемы - экономный расход оперативной памяти.
Случай 
с взаимно простыми сомножителями
Рассмотрим другой крайний случай, когда и 
. В этом случае существуют целые 
, для которых 
. Отсюда следует, что
(1)
При этом можно считать выполненными неравенства
.(2)
Если такое неравенство для 
, например, не имеет места, можно разделить на 
. Для
любого целого 
из (1) вытекает
. При ограничениях типа (2) 
находятся однозначно. Имеем
. Числа 
- взаимно простые. Следовательно имеем для любого целого 
. Теперь 
. Раскрывая скобки и отбрасывая члены кратные , получим показатель вида 
.
Из равенства 
следует, что 
, поэтому весь показатель сравним с 
. Это означает, что 
. Вводя обозначения 
, окончательно получим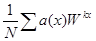 
=
. Это означает, что преобразование Фурье для точек свелось к последовательному выполнению преобразования Фурье по 
точкам, а затем - по точкам результатов предыдущего преобразования. При этом потребуется не более, чем 
умножений. По сравнению с 
выигрыш небольшой. Если же для какого-либо из промежуточных случаев есть своя быстрая схема, выигрыш может получиться значительным.
Свертка последовательностей и ее вычисление
Сдвиг последовательности
Пусть имеется последовательность 
. Мы можем превратить ее в бесконечную последовательность, положив 
. Выберем целое 
и определим 
. Найдем связь между преобразованиями Фурье этих последовательностей. Имеем
(1)
Циклическая свертка
Пусть имеются последовательности .и 
. Определим их свертку
(2)
Операция свертки является коммутативной, и кроме того, последовательность, определенная формулой (2), автоматически будет периодической с периодом . Назовем ее циклической сверткой исходных последовательностей. Подсчитаем конечное преобразование Фурье.
(3)
Таким образом, преобразование Фурье от свертки равно произведению преобразований Фурье от сомножителей.
Использование окон
На практике мы имеем дело с исходными последовательностями большой длины, а дискретное преобразование Фурье применяем лишь к отдельным частям. В этом случае эта отдельная часть трактуется как периодическая последовательность, что приводит к искажению результатов. Например, исходная последовательность имеет вид 1,2,3,... Предположим, мы решили ограничиться значениями 
. Выбрав первые четыре члена, получим последовательность 1,2,3,4,1,2,3,..У этой последовательности имеется скачок при переходе от 4 к 1, чего нет в исходной последовательности. Для того, чтобы ослабить указанный эффект, используют сглаживающие окна, которые превращают конечную последовательность в периодическую без скачков на концах. Пусть 
последовательность, для которой 
, тогда у последовательности 
не возникает скачка из-за периодического продолжения. Эту последовательность называют сглаживающим окном. Согласно (3), 
. Обычно в качестве окон используют те же окна Хэмминга и Хеннинга, о которых шла речь выше.
Кратковременное преобразование Фурье
Пусть имеется исходная последовательность 
большой длины. Требуется изучить ее спектр с помощью ДПФ. Это означает, что на самом деле будет исследована лишь часть последовательности длины . Выбирают окно соответствующей длины, после чего, передвигая окно вдоль последовательности, получим набор спектральных коэффициентов, зависящих от положения окна. Это и есть кратковременный спектр. В этом смысле процедура напоминает Wave-let преобразование. Выбор длины окна является компромиссом между точностью и разрешающей способностью. Чем длиннее окно, тем больше коэффициентов будет найдено, но при этом будут получены усредненные по длине окна характеристики.
Рекомендуемая литература:
1. Глинченко, А. С. Цифровая обработка сигналов: курс лекций. – Красноярск: СФУ, 2008.
2. Глинченко, А. С. Цифровая обработка сигналов: уч. пособие. – 2-е изд., перераб. и доп. – Красноярск: ИПЦ КГТУ, 2005. – 482 с.
3. Глинченко, А. С. Лабораторный практикум по цифровой обработке сигналов: учеб. пособие. – Красноярск: СФУ, 2008.
6. Глинченко, А. С., Голенок А. И. Принципы организации и программирования сигнальных процессоров семейства ADSP-21XX: учеб.-метод. пособие. – Красноярск: ИПЦ КГТУ, 2000. – 88 с.
7. Сергиенко А. Б. Цифровая обработка сигналов: учеб. пособие. – 2-е изд. – СПб.: Питер, 2006. – 751 с.
8. Основы цифровой обработки сигналов: Курс лекций /
А. И. Солонина, Д. А. Улахович., С. М. Арбузов, Е. Б. Соловьева. – СПб.: БХВ-Петербург, 2005. – 768с.