Теория была сформулирована С. Аррениусом в 1889 году. В основе этой теории лежит представление о том, что для протекания химической реакции необходимо соударение между молекулами исходных веществ, а число соударений определяется интенсивностью теплового движения молекул, т.е. зависит от температуры. Но не каждое соударение молекул приводит к химическому превращению – к нему приводит лишь активное соударение.
Тот минимальный запас энергии, которым должны обладать молекулы исходных веществ для того, чтобы их соударение было активным, называют энергетическим барьером реакции. Наглядное представление об энергетическом барьере реакции дает графическое изображение энергетики химической реакции (рис. 8.4).
В качестве абсциссы в этих диаграммах используется так называемая координата реакции. Вообще говоря, она является сложной функцией межатомных расстояний. Но для практических целей и простых молекул можно считать, что она характеризует изменения в межатомных расстояниях, которые происходят при сближении исходных молекул, образующих активированный комплекс, и взаимном удалении продуктов реакции при распаде активированного комплекса. По оси ординат откладывается потенциальная энергия всей системы.
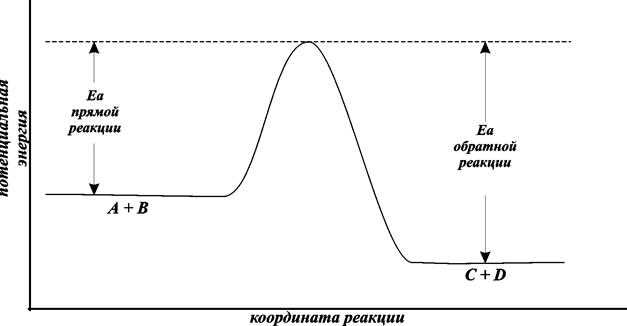
Рис. 8.4. Энергетическая диаграмма реакции А+B = C+D
То дополнительное количество энергии, которое нужно добавить к средней энергии молекул исходных веществ, чтобы соударение стало активным, называется энергией активации.
Энергия активации ощутимо влияет на значение константы скорости реакции и ее зависимости от температуры: чем больше Еа, тем меньше константа скорости и тем значительнее влияет на нее изменение температуры. Константа скорости реакции связана с энергией активации сложной зависимостью, описанной уравнением Аррениуса:
|
|
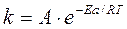, (8.27)
где А – так называемое «число соударений», которое представляет собой число соударений в одну секунду между одной молекулой вещества а и одной молекулой вещества В, заключенных в объеме в 1см3.
Однако наблюдаемые константы скорости реакции, как правило, гораздо меньше вычисленных по уравнению. Поэтому уравнение для константы скорости реакции видоизменяют следующим образом:
, (8.28)
где Z – теоретическое число столкновений, а Р – так называемый фактор вероятности или стерический, который учитывает все влияния, вызывающие отклонения от идеального уравнения. Необходимость ориентации может заметно тормозить даже сравнительно простые реакции. Хорошо изученным примером является реакция Н2 + J2 ® 2НJ.
Для того, чтобы простое соударение дало две молекулы йодистого водорода, надо, чтобы ориентация молекулы была сходна с той, которая изображена на рис. 8.5 а.
Рис. 8.5. Схема, отображающая значение благоприятной ориентации для того, чтобы простое соударение могло привести к образованию продукта реакции
Энергия активации этой реакции невелика, но скорость мала. Это связано с довольно жесткими требованиями, предъявляемыми к ориентации реагирующих молекул. Тогда А = РZ, т.е. а характеризует число соударений с благоприятной ориентацией и называется предэкспоненциальным множителем.
Используя уравнение Аррениуса, можно определить энергию активации Еа. Для этого уравнение Аррениуса удобно применять в логарифмической форме:
|
|
(8.29)
или
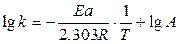. (8.30)
Если построить график lg k от 1/ Е, то получим прямую, отсекающую на оси ординат отрезок, равный lg А, и имеющую тангенс угла, равный ‑ Еа /2,303 R, т.е. tga = - Еа /2,303 R, откуда Еа = -2,303 R tga.
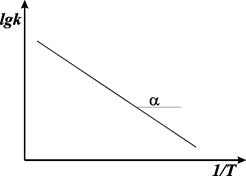
Рис. 8.6. График Аррениуса
Из уравнения видно, что константа скорости реакции k является произведением двух сомножителей. Предэкспоненциальный множитель А практически не зависит от температуры, так как последняя не влияет на взаимную ориентацию молекул. Экспоненциальный множитель e -Ea/RT, который характеризует долю активных соударений от общего числа двойных соударений, сильно зависит от температуры.
Теория активных соударений внесла в химическую кинетику новые представления об активных соударениях и об энергии активации, но эта теория не рассматривала механизм самого соударения, что является ее недостатком.
8.15.2. Теория активированного (переходного) комплекса
(переходного состояния)
Эта теория – простейший и исторически первый вариант статистической теории химических реакций. Она разработана Э. Вагнером, М. Поляни, Г. Эйрнингом и М. Эвансом в 30-х годах XX века.
8.15.3. Вывод основного уравнения теории
переходного состояния
В основу теории также положено представление о столкновении молекул как непременном условии реакции. Но она рассматривает то, что происходит в момент столкновения.
Для реакции А + В = С в соответствии с теорией переходного состояния следует: А + В «х* ® С, где х* – переходной комплекс (пк). Что подразумевается под переходным комплексом? После столкновения молекул А и В начинается перераспределение химических связей и образование переходного комплекса. переходный комплекс представляет такое состояние взаимодействующих молекул, когда старые связи еще не полностью разорвались, а новые еще не полностью сформировались. В результате мы имеем состояние промежуточное между А, В и С. Переходное состояние характеризуется непрерывным изменением расстояний между взаимодействующими атомами. В этом существенное отличие переходного комплекса от обычной молекулы, в которой средние расстояния между атомами не зависят от времени. Переходный комплекс также не следует путать с промежуточными веществами. Он является динамической структурой, для образования которой требуется затрата энергии. Энергия, необходимая для перевода реагирующих молекул в состояние переходного комплекса, носит название энергии активации. Так как исходные молекулы еще не распались, то энергия перехода в активированное состояние меньше энергии разрыва связей в молекулах исходных веществ:
|
|
Еа < Едиссоциации.
Таким образом, формирование переходного комплекса – процесс энергетически более выгодный, чем полный распад вступающих в реакцию молекул. С другой стороны, превращение активированного комплекса в продукты реакции всегда является экзотермическим процессом.
Основной постулат теории переходного состояния заключается в том, что исходные вещества всегда находятся в равновесии с переходным комплексом:
А + в «х* ® С.
В этом случае k химического равновесия переходного комплекса равна:
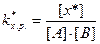, (8.31)
а концентрация х составит:
. (8.32)
Затем ПК распадается необратимо с образованием продукта С. Характеристикой (количественной) распада будет частота распада ПК – Р. Из статистической механики известно, что Р зависит только от температуры. Эта зависимость имеет вид Р = kТ / h, где k – постоянная Больцмана; h – постоянная Планка; Т – абсолютная температура.
Значит, для данной температуры число Р одинаково для всех переходных состояний, а скорость любой химической реакции определяется лишь концентрацией ПК:
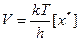. (8.33)
Концентрация ПК связана с концентрацией реагентов и поэтому, подставив их выражения, получим:
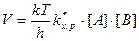. (8.34)
К элементарной реакции взаимодействия применим закон действия масс:
V = kV[А][B], (8.35)
символ k V употребляется для константы скорости в отличие от константы Больцмана.
Приравняем правые части уравнений и получим:
(8.36)
или
. (8.37)
Из уравнения видно, что при данной температуре константа скорости реакции зависит от константы химического равновесия образования ПК и от частоты распада ПК. Уравнение называется основным уравнением теории переходного состояния.
8.15.4. Термодинамическая форма основного уравнения теории
переходного состояния
Термодинамические данные позволяют связать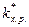 
со стандартной свободной энергией образования переходного комплекса D G ¹, называемой также свободной энергией активации:
DG’¹ = -RT ln 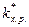, (8.38)
откуда
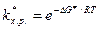. (8.39)
Тогда для константы скорости химической реакции можно записать
. (8.40)
Из этого уравнения видно, что скорость реакции определяется свободной энергией активации D G ¹, а не Еа, как это следует из теории активных соударений Аррениуса.
Поскольку D G ¹ = D Н ¹ - Т D S ¹, то
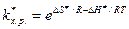(8.41)
или, по теории переходного состояния, kv равна:
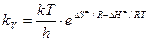(8.42)
или
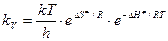, (8.43)
т.е. мы получили термодинамическую форму основного уравнения теории переходного состояния.
8.15.5. Сравнение термодинамической формы
основного уравнения теории переходного состояния
с уравнением Аррениуса
При сравнении уравнения для ТПС с уравнением Аррениуса обнаруживается, что
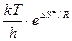(8.44)
и соответствует А в уравнении Аррениуса, т.е.
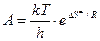. (8.45)
Значит определив опытным путем А, можно рассчитать энтропию активации D S ¹, которая дает важную информацию о механизме образования активированного комплекса. Например, чем более жестко связывается фермент с субстратом, т.е. образуется большее число связей, тем больше уменьшается D S ¹. Величина D Н ¹ практически равна энергии активации.
Поскольку А=РZ, то:
. (8.46)
Так как Z – теоретическое число столкновений и kT / h практически постоянны, вероятностный фактор Р будет, очевидно, связан с энтропией активации D S ¹. Если она велика и положительна, то фактор Р велик, и реакция будет быстрой. Но если D S ¹ отрицательна и мала, то реакция будет медленной, т.е. чем больше возрастание энтропии, тем больше вероятность переходного состояния.
Поскольку kT / h соответствует Z и равно при 298К 6,3× 10-12 сек-1, то это число равно числу активных комплексов, разлагающихся за 1 сек. в 1 см3 или количеству соударений в 1 сек. в 1 см3.
Таким образом, скорость реакции, согласно теории переходного состояния, зависит от двух факторов:
1) энергетического фактора – D Н ¹, энтальпии активации (чем больше энтальпия активации, тем меньше скорость реакции);
2) энтропийного фактора – D S ¹, энтропии активации (чем больше энтропия активации, тем больше скорость реакции).
Учет энтропийного фактора для кинетики реакций во многих отношениях оказался плодотворным и впервые позволил установить связь константы скорости со строением молекул реагирующих веществ. При этом теория ПС оперирует, в частности, величинами расстояний между атомами в молекулах, взаимной ориентацией молекул, т.е. параметрами геометрического характера.
Теория активных соударений позволяет при знании энергии активации рассчитать общее число эффективных соударений и отсюда скорость реакции, не объясняя механизма реакции. В отличие от теории активных соударений теория ПК сопоставляет различные возможные комплексы, выявляет большую или меньшую их достижимость и определяет в результате энергетически наиболее выгодный путь реакции.
Для вычисления скоростей взаимодействия двух атомов две теории дают одинаковые результаты. В случае нелинейных многоатомных молекул теория ПК дает значение скоростей, отличных от значений, которые дает теория соударений. Если известна конфигурация реагирующих молекул и активного комплекса, теория ПК позволяет рассчитать предэкспоненциальный множитель. К сожалению, в большинстве случаев строение активированного комплекса и его свойства неизвестны и это затрудняет расчеты.
Таким образом, две теории дополняют друг друга. Теория ПК применяется для вычисления абсолютных скоростей электродных процессов, процессов диффузии и т.д. Теория активных соударений хорошо описывает, как правило, реакции в газовой среде.
Лекция 9.
Основы кинетики и механизма
ферментативных реакций.
Гомогенный и гетерогенный катализ
9.1. Понятие катализа
Катализ (от греч. katalysis – разрушение) – изменение скорости химической реакции под влиянием катализаторов. Обычно под катализом понимают ускорение реакции (положительный катализ), однако в отдельных случаях подразумевается замедление реакций (отрицательный катализ). Реже приходится иметь дело с явлением автокатализа, когда катализатором служит один из продуктов реакции.
В зависимости от того, находится ли катализатор в той же фазе, что и реагирующие вещества, или образует самостоятельную фазу, говорят о гомогенном или гетерогенном катализе. В последнем случае ускорение процесса обычно связано с каталитическим действием поверхности твердого тела (катализатора). В гетерогенном катализе применяются переходные металлы, их оксиды, сульфиды и другие соединения. Гомогенными катализаторами обычно служат растворы кислот, оснований, солей и, прежде всего, солей d-элементов (Cr, Mn, Fe, Co, Ni, Cu и др.)
В ходе каталитической реакции катализатор остается химически неизменным, а его масса – постоянной (если не считать потерь за счет механического уноса и возможности протекания побочных химических процессов, в которых катализатор участвует как реагент). Между количествами реагентов и катализаторов существует огромная диспропорция. Так, одна массовая часть катализатора вызывает превращение миллиона массовых частей NH3 при его окислении в азотную кислоту.
Катализаторы отличаются избирательностью (селективностью) действия. Так, на оксиде алюминия при 350-360 °С происходит дегидратация этанола:
С2Н5ОН ® СН2 = СН2 + Н2О,
а в присутствии меди при 200-250 °С – его дегидрирование:
С2Н5ОН ® СН3СНО + Н2.
В отсутствие катализатора обе реакции идут параллельно.
Катализатор не влияет на истинное равновесие, т.е. не меняет константу равновесия и равновесные концентрации. Он в равной мере ускоряет и прямую и обратную реакции. Если повышение температуры не только ускоряет процесс, но и смещает равновесие, то катализатор лишь изменяет время его достижения. Оно тем меньше, чем активнее катализатор. Вводя катализатор в реакционную зону эндотермических реакций, можно осуществить снижение температуры, не проигрывая в скорости процесса.
Присутствие в зоне реакции посторонних веществ оказывает различное влияние на катализатор: одни нейтральны, другие усиливают действие катализатора, третьи его ослабляют и вообще прекращают. Ускорители каталитических процессов называются промоторами, или активаторами. Вещества, снижающие скорость реакции, называются ингибиторами.
9.2. Основы теории гомогенного катализа
Большинство гомогенных каталитических процессов объясняет теория промежуточных соединений. Исходное положение этой теории – предположение, что в течение реакции образуются неустойчивые, промежуточные соединения катализатора с реагирующими веществами, которые затем распадаются с образованием продуктов реакции, а катализатор регенерируется.
Так, для гипотетической реакции А + В ® С механизм протекания таков: на первой стадии образуется неустойчивое промежуточное соединение одного из реагентов с катализатором: А + К® [АК]. Затем это соединение взаимодействует с другим исходным веществом, в результате чего образуется продукт реакции, а катализатор освобождается: [AK] + В ® С + К.
Хотя участие катализатора в механизме реакции и удлиняет путь процесса, скорость его значительно увеличивается, так как энергетические затраты на образование и разрушение промежуточных соединений гораздо меньше, чем непосредственное, прямое образование продуктов реакции, – иными словами, влияние катализатора на скорость химического процесса связано с понижением энергии активации реакции.
При гомогенном катализе важное значение имеет кратковременное сочетание молекул и ионов, в результате чего образуются соединения типа диполей или содержащие водородную связь. Эти реакции могут катализироваться кислотами или основаниями. Согласно протонной теории кислот и оснований, кислота – это соединение, способное отщеплять протон, основание – вещество, способное присоединять протон. В ходе катализа происходит перераспределение электронов в молекуле субстрата, возникают промежуточные соединения с повышенной активностью (карбониевые ионы, карбанионы, полярные комплексы). При этом снижается энергия активации и ускоряется реакция.
Кислотно-основной катализ обязательно включает стадию переноса протона от одной молекулы к другой. В реакционной среде должны быть доноры и акцепторы. Если кислоту обозначить НА, субстрат – НХ, а В и А- – основания, НХН+ и Х - – ионизированные формы субстрата, ХН – продукты реакции, то катализ кислот можно записать следующим образом:
НХ + на «НХН ++ А-
В + НХН+ «ВН+ + ХН
ВН+ + А- «в + НА;
катализ оснований:
В + НХ«ВН+ +Х-
Х- + на «ХН +А-
ВН+ + А- «в + НА.
Гомогенных каталитических реакций в растворах, ускоряемых ионами гидроксила и водорода, довольно много. К этому типу относятся реакции этерификации, инверсии сахаров, омыление сложных эфиров и т.д.
Омыление сложных эфиров катализируется как кислотой, так и основанием. В последнем случае оно протекает по уравнению 2-го порядка и может быть записано:
СН3СООС2Н5 + ОН- ® СН3СОО- + С2Н5ОН.
9.3. Основы теории гетерогенного катализа
Одно из современных объяснений механизма действия твердых катализаторов дает мультиплетная теория. Она была предложена в 1929 году А.А. Баландиным. В основу мультиплетной теории положены принципы структурного и энергетического соответствия между поверхностью катализатора и молекулами реагирующих веществ. Структурное соответствие заключается в том, что расстояние между атомами кристаллической решетки катализатора и валентные углы между ними должны соответствовать этим же параметрам участвующих в реакции веществ. В таком случае молекулы реагирующих веществ совершают активированную адсорбцию на катализаторе, которая состоит в том, что образуется множество связей между атомами адсорбента (катализатора) и адсорбтива (реагирующего вещества). При этом происходит «ослабление» внутримолекулярных связей реагирующих веществ – активация.
Например, расстояние между атомами Ni – Ni на поверхности никеля Ренея наилучшим образом подходит к ацетиленовой связи, а к этиленовой связи в равной мере подойдут расстояния между атомами многих металлов – от платины до железа. Вот поэтому никель Ренея обладает уникальной селективностью по отношению к реакциям гидрирования ацетиленовых углеводородов, а металлы платиновой группы используются в процессах получения соединений этилена.
Эту теорию можно было бы назвать теорией геометрического подобия активного центра и реагирующей молекулы. Для различных реакций число адсорбционных центров (каждый из которых отождествляется с одним атомом металла) в активном центре принимается равным 2, 3, 4, 6 и т.д. Подобные активные центры были названы дуплетами, триплетами, квадриплетами, секстетами, а в общем случае мультиплетами.
Поверхностное соединение, образующееся в результате активированной адсорбции молекул реагирующих веществ на отдельном мультиплете, называют мультиплетным комплексом. Он отображает физическое состояние вещества в момент его превращения (исходные вещества прекратили свое существование, а продукты реакции еще не образовались). Мультиплетный комплекс распадается с образованием или продуктов реакции, или исходных веществ. Этим управляют законы химического равновесия.
Согласно другому принципу мультиплетной теории – энергетическому соответствию – наибольшая эфективность твердого катализатора достигается при определенной энергии мультиплетного комплекса, соответствующей равенству поверхностных активностей исходных веществ и продуктов реакции по отношению к данному катализатору.
Энергетическое соответствие катализатора определяют экспериментально, поэтому мультиплетная теория не в состоянии однозначно предсказать катализатор той или иной реакции.
В отличие от мультиплетной теории, теория каталитически активных ансамблей Н.И. Кобозева предусматривает возможность существования активных центров из атомов, не входящих в кристаллическую решетку. Из этой теории следует, что лишь сочетание определенного (обычно небольшого) числа частиц катализатора (ансамбль) способно проявлять «катализаторскую» активность.
Так, для реакции соединения азота и водорода необходимо три атома катализатора (железа), сгруппированных в активный ансамбль. Для реакции присоединения водорода к органическим соединениям, ускоряемой палладием, необходимо два атома палладия и т.д. Отдельные ансамбли на поверхности твердого катализатора не могут соединяться друг с другом, потому что поверхность катализатора очень неоднородна, и частицы вещества не могут беспрепятственно двигаться по всей поверхности. Их движение ограничено лишь небольшой частью поверхности. Согласно теории каталитически активных ансамблей, атомы активных центров образуют «аморфную» фазу на поверхности кристаллических граней самого металла. Последний выполняет при этом роль носителя.
9.4. Ферменты как биологические катализаторы
Химические процессы в живых организмах осуществляются при помощи биологических катализаторов – ферментов. Все известные в настоящее время ферменты являются белками, многие из которых содержат ионы металлов.
По эффективности ферменты значительно превосходят химические катализаторы. Во многом это обусловлено тем, что ферменты резко снижают энергетические барьеры на реакционном пути. Например, энергия активации для реакции распада перекиси водорода под действием иона железа (II) и молекулы каталазы соответственно 42 и 7,1 кДж/моль, для гидролиза мочевины кислотой и уреазой – 103 и 28 кДж/моль соответственно.
Кроме того, ферменты отличает высокая специфичность и направленность действия. Так, амилаза, содержащаяся в слюне, легко и быстро расщепляет крахмал, молекула которого состоит из большого числа одинаковых глюкозных звеньев. Но она не катализирует процесс распада сахарозы.
Каталитические действия ферментов происходят в сравнительно «мягких» условиях (t = 37–40oC, при невысоком давлении и определенном значении рН).
9.5. Кинетика реакций, катализируемых ферментами
Уже в ранних исследованиях по влиянию концентрации реагента на скорость ферментативных реакций была обнаружена очень важная особенность ферментативного катализа, которая заключается в сложном характере кинетики этих реакций. Так, при низких концентрациях реагента (или субстрата) реакция протекает в соответствии с уравнением первого порядка. При высоких концентрациях субстрата скорость перестает зависеть от концентрации и, таким образом, реакция в этих условиях протекает в соответствии с уравнением нулевого порядка. Общий вид зависимости скорости реакции от концентрации субстрата при такой двухступенчатой кинетике приведен на рис. 9.1.
Рис. 9.1. Зависимость скорости реакции, катализируемой ферментом, от концентрации субстрата
Л. Анри первым предположил, что фермент образует промежуточное соединение или комплекс с субстратом. При высоких концентрациях субстрата весь фермент будет в комплексе с субстратом и скорость реакции будет максимальной. Иными словами, в реакциях, катализируемых ферментами, стадией, определяющей скорость процесса, будет стадия распада комплекса на фермент и продукт. Она носит название лимитирующей стадии всего процесса.
Обозначим фермент Е, а субстрат S и запишем уравнение ферментативной реакции.
Образование комплекса:
(быстрая стадия). (9.1)
Распад комплекса:
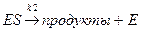(медленная стадия), (9.2)
V1 = k2 [ES]. (9.3)
Такие реакции как в химической, так и ферментативной кинетике носят название сложных. Их можно решать как равновесным, так и методом стационарного состояния.
Равновесный метод дает хорошие результаты, если состояние, близкое к равновесному, устанавливается на быстрой стадии. Именно этим методом Михаэлис и Ментен провели математическую обработку экспериментальных данных, подобных представленным на рис. 9.1. Сложность решения заключается в том, что необходимо выразить концентрацию равновесную [ ES ] через величины, которые можно измерить количественно. Это позволяет исключить [ ES ] из уравнения скорости реакции. Константа равновесия первой стадии может быть представлена в виде
. (9.4)
Следовательно
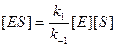. (9.5)
На этом этапе задача еще не решена, потому что [ E ] – это концентрация свободного фермента, которую также трудно измерить экспериментально. Однако в состоянии равновесия содержание Е своб. и Е связ. можно выразить через Е t, где Е t – общая концентрация фермента:
[Et] = [Eсвоб.] + [ES]. (9.6)
Это уравнение носит название уравнения постоянства общей концентрации фермента. Общая концентрация фермента может быть измерена. Множитель в уравнении (9.5) можно заменить на разность [ E t] – [ ES ]. В результате уравнение примет вид
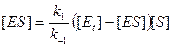. (9.7)
Решая его относительно [ ES ], получим:
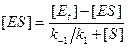. (9.8)
Вместо k -1/ k 1 введем К М. Новая константа по своей сути является константой диссоциации фермент/субстратного комплекса ES, в то время как К, входящая в уравнение (9.4), является константой его образования. Новую константу, численно равную отношению k -1/ k 1, называют константой Михаэлиса и обозначают обычно как К м. Тогда уравнение (9.8) принимает вид
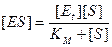. (9.9)
Теперь мы имеем выражение, которое можно подставить в общее уравнение скорости: V = k 2 [ ES ] и получим
. (9.10)
Сделаем еще одно упрощение: когда весь фермент связывается с субстратом (при высокой концентрации субстрата), скорость становится максимальной. Свободного фермента уже нет и [ E t] = [ ES ]. В этих условиях скорость реакции обозначают V max. Величина V max является константой, характеризующей реакцию в условиях, когда она протекает по уравнению нулевого порядка. Это уравнение имеет вид
Vmax= k2[Et],
и тогда уравнение (9.10) примет вид
.
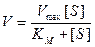В результате такой подстановки мы имеем уравнение Михаэлиса-Ментен, позволяющее легко измерять максимальную скорость из экспериментальных данных, тогда как величины E t и k 2 определять сложнее.
Конечно, сегодня имеется ряд очищенных ферментов с известным молекулярным весом и для них можно рассчитать молярную концентрацию E t. Но для всех неочищенных препаратов, а также для ферментов с неизвестным молекулярным весом применение V max вместо k 2[ E t] существенно упрощает расчеты.
Действительно, по этому уравнению, если концентрация S мала по сравнению с К М, то член [ S ] можно исключить из знаменателя, и уравнение Михаэлиса-Ментен приобретает вид
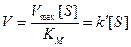(первый порядок).
При высоких концентрациях субстрата можно считать, что величина [ S ] значительно больше К М. При этом
V = Vmax = const (нулевой порядок).
Считается, что при изучении многих реакций, катализируемых ферментами, лучше пользоваться не равновесным методом, а методом стационарного состояния. Рассмотрим, как в этом случае будут различаться окончательные уравнения скорости.
Начальные стадии в обоих вариантах одинаковы:
;
;
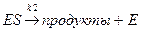скорость = k2[ES].
После достижения стационарного состояния [ ES ] будет постоянна и, следовательно, скорость ее изменения будет равна нулю:
d[ES]/dt = 0 = k1[E][S] – (k –1[ES] + k2[ES]) (9.11)
образование исчезновение
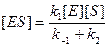. (9.12)
Различие между выражением (9.12) и (9.5) заключается в константах: равновесный метод дает член k 1/ k –1, а метод стационарного состояния – член k 1/(k –1 + k 2). Обратной величиной последнего будет новая константа, а именно константа Михаэлиса К М в условиях стационарного состояния. Все остальные преобразования аналогичны первому случаю. Окончательная форма записи уравнения скорости в условиях стационарного состояния реакции имеет вид
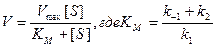. (9.13)
Это и есть уравнение скорости, которое применяется в ферментативной кинетике, если нет убедительных данных, свидетельствующих о том, что начальная стадия реакции быстро приходит к равновесию.
Поскольку уравнения (9.13) и (9.11) являются уравнениями гиперболы, графически определить постоянные величины К m и V max довольно трудно, поэтому уравнение Михаэлиса-Ментен было преобразовано в другие более удобные формы. Одна из них – форма уравнения Лайнуивера-Берка. Если уравнение (9.13) записать в обычной форме, а затем обе стороны уравнения выразить в виде обратных величин, то получаем равенство
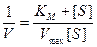. (9.14)
Правую часть уравнения можно представить так:
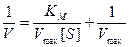. (9.15)
Две переменные V и [ S ] теперь разделены, и если построить график в координатах (1/ V,1/[ S ], то мы получим прямую линию с наклоном, равным К m/ V max, пересекающую ось 1/ V в точке 1/ V max.
Однако для некоторых ферментативных систем график, построенный в этих координатах, может отличаться от прямой линии. Это, возможно, обусловлено тем, что при избыточных концентрациях субстрата фермент может ингибироваться или активироваться субстратом. Для аллостерических ферментов кривые насыщения субстратом обычно имеют сигмоидную форму и часто могут быть описаны уравнением, в котором [ S ] заменено на [ S ]n. Если аномалии появляются экспериментально при низких концентрациях субстрата, то соответствующие точки будут находиться только в правой части графика. Следовательно, эти аномалии не должны мешать расчету величин K m и V max. Если же отклонения от линейности обнаруживаются при высоких концентрациях субстрата, то соответствующие точки будут находиться рядом с точкой пересечения и возникнет проблема с экстраполяцией линейных участков полученной кривой. В таких случаях может быть использована другая форма уравнения Лайнуивера-Берка. Для этого умножим обе части уравнения (9.15) на [ S ] и получим:
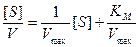. (9.16)
Построение графика в координатах [ S ]/ V и S дает прямую линию с наклоном, равным 1/ V max, пересекающую ось [ S ]/ V в точке K m/ V max. Все отклонения от графика, проявляющиеся при больших значениях [ S ], будут находиться в правой части графика и с ними можно не считаться.
Упомянем еще об одной часто применяемой альтернативной форме уравнения Михаэлиса-Ментен, поскольку она обладает тем преимуществом, что позволяет заметить такие отклонения от линейности, которые могли быть пропущены в случае других графиков.
Если умножить уравнение (9.15) на V max· V и произвести соответствующие преобразования, то получим:
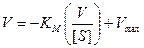. (9.17)
Отметим, что точка пересечения прямой с осью ординат соответствует V max, точка пересечения с осью абсцисс соответствует величине V max/ K m, а наклон прямой равен – K m.
В настоящее время для анализа кинетических параметров ферментативных реакций все больше используется ЭВМ, что расширяет перечень подходов и делает анализ более объективным.
9.6. Физический смысл величин Km и Vmax
Как правило, для характеристики каждого фермента определяют его константу Михаэлиса, которая легко воспроизводится и не зависит от концентрации фермента. Физический смысл этой константы заключается в том, что она численно равна концентрации субстрата, при которой активность фермента составляет половину максимальной. Это легко показать с помощью небольшого алгебраического преобразования, подставив вместо V величину 0,5 V max:
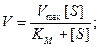
. (9.18)
Разделим (9.18) на V max и получим:
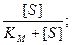
0,5Кm + 0,5[S] = [S]
или
Кm = [S].
Поэтому K m имеет размерность моль/л.
Фундаментальное значение величины V max связано с ее отношением к величине k 2. Для специального случая, когда весь фермент входит в комплекс ES, мы можем заменить величину k 2[ E t] на V max.
Скорость = k2[Et] = Vmax.
Если концентрация фермента выражена в моль/л, а скорость превращения субстрата – моль/л мин., то k 2 равна максимальному числу оборотов фермента:
.
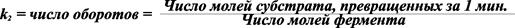Поскольку скорость реакции зависит от температуры, число оборотов относят к какой-то конкретной температуре. Для определения числа оборотов необходимо знать молекулярный вес фермента и его концентрацию в растворе. При этом необходимо помнить, что все эти расчеты относятся к ферментам с одним активным центром. Очень часто число оборотов рассчитывают по количеству образовавшегося продукта.
9.7. Уравнение Михаэлиса-Ментен
и ферментативные механизмы
Изучение механизма реакции по уравнению Михаэлиса-Ментен не всегда свободно от недостатков. Самым явным из них является предположение о том, что существует только один промежуточный комплекс – ES. По-видимому, более близкий к истинному механизм можно записать уравнением
. (9.19)
Определение величин наклона кривой и точки пересечения по методу Лайнуивера-Берка позволяет найти константы k m и V max. Однако если механизм достаточно сложен, то в величину k m входят добавочные константы скорости реакции, и в этом случае интерпретировать ее трудно. Поэтому интерпретацию механизма ферментативной реакции лишь на основании линейности графиков Лайнуивера-Берка необходимо проводить с большой осторожностью.