Sn2+ + 2e- «Sn
Cl2 + 2e- «2Cl-.
Sn2+ + 2Cl- «Sn + Cl2
Потенциал правого электрода равен
. (11.25)
Потенциал левого электрода равен
. (11.26)
ЭДС цепи составляет
, (11.27)
Так как 
представляет собой среднюю ионную активность электролита, то
,
т.е. ЭДС простой химической цепи зависит от природы электродов и от средней ионной активности электролита. К сложным электрохимическим системам относятся системы, в которых одинаковые или различные металлические электроды погружены в различные по составу электролиты:
(-) Zn | ZnSO4 || CuSO4 | Cu (+).
На электродах протекают следующие реакции:
Zn ® Zn2+ + 2e-;
Cu2+ + 2e- ® Cu.
E цепи равна
. (11.28)
ЭДС сложных химических цепей определяются разностью стандартных потенциалов электродов и активностью потенциал-определяющих ионов (т.е. ионов, обратимых по отношению к электродам).
11.5. Концентрационные цепи
Различают два типа концентрационных элементов – с переносом и без переноса ионов. Концентрационный элемент с переносом ионов состоит из двух одинаковых металлических пластинок, погруженных в раствор с различными концентрациями ионов данного металла. Растворы либо разделены пористой перегородкой, проницаемой для ионов, либо при нахождении в разных сосудах, соединенных электролитическим ключом. Например, левый медный электрод погружен в более концентрированный раствор С1 > С2 и приобретает более положительный потенциал, чем правый:
Cu ® Cu2+ + 2e-
Cu2+ + 2e- ® Cu
Cu + Cu2+ ® Cu2+ + Cu.
Движущей силой в этом элементе является разность концентраций. При его работе медный электрод растворяется в менее концентрированном растворе, а в более концентрированном ионы меди разряжаются и внедряются в металл. Это приводит к выравниванию концентраций, за счет чего и возникает электрическая энергия. Работа процесса, связанная с выравниванием концентраций, равна
|
|
. (11.29)
Эта работа полностью превращается в электрическую энергию 
. Отсюда
. (11.30)
Концентрационные элементы без переноса ионов состоят из двух электродов – твердых сплавов или амальгам, отличающихся по содержанию активного вещества. Оба электрода погружены в один и тот же раствор, содержащий ион активного вещества. В этих элементах существует граница между жидкими фазами и нет диффузионного потенциала, искажающего результаты измерения ЭДС.
Примером такого элемента может служить кадмиевый амальгамный элемент.
В этом случае происходит перенос кадмия от более концентрированной амальгамы к менее концентрированной. ЭДС такого элемента (при 
) равна
. (11.31)
Эта формула справедлива, если металлы, входящие в состав сплава (или амальгамы), не образуют химических соединений.
Лекция 12.
Поверхностные явления и адсорбция
12.1. Общая характеристика поверхностных явлений
К поверхностным явлениям относится совокупность явлений, связанных с особенностями свойств пограничных слоев между двумя соприкасающимися фазами, обусловленных наличием избыточной энергии у поверхности раздела. Эти явления могут быть разделены на две основные группы. К первой группе следует отнести явления, связанные с изменением формы поверхностей раздела (капиллярные явления, смачивание, прилипание и др.). Ко второй группе относятся адсорбированные явления, в основе которых лежит изменение состава поверхностного слоя.
Молекулы вещества, расположенного внутри фазы, отличаются по энергетическому состоянию от молекул, находящихся на границе раздела фаз.
|
|
Во внутренних слоях фазы силы взаимодействия для каждой молекулы в среднем по времени одинаковы по всем направлениям, полностью скомпенсированы и их равнодействующая равна нулю. Поэтому произвольное перемещение молекулы жидкости или газа внутри фазы в любом направлении не связано с выделением или поглощением энергии. Иначе обстоит дело с молекулами, находящимися на границе раздела фаз. Они испытывают неодинаковое влияние сил межмолекулярного взаимодействия со стороны каждой из соседних фаз, поскольку их физические свойства (плотность, поляризуемость и т.д.) различны.
Поверхностная молекула на границе жидкость/пар испытывает одностороннее притяжение со стороны жидкости, втягивающее ее внутрь жидкости.
В общем случае равнодействующая сил межмолекулярного взаимодействия поверхностных молекул перпендикулярна поверхности раздела и направлена в сторону фазы с более интенсивным межмолекулярным взаимодействием. Эта сила, отнесенная к единице площади поверхности раздела, носит название внутреннего давления. Как правило, внутреннее давление тем больше, чем выше полярность вещества. Втягивая поверхностные молекулы внутрь фазы, внутреннее давление стремится уменьшить поверхность до минимума, возможного в данных условиях.
Увеличение площади поверхности раздела фаз связано с выделением молекул из глубины фазы на поверхность, т.е. с совершением работы против сил внутреннего давления. Эта работа W в обратимых изотермических условиях пропорциональна площади образующейся новой поверхности S:
|
|
-dW = sdS. (12.1)
Максимальная работа W, взятая со знаком минус, в зависимости от условий (р = соnst, или V = const) равна увеличению энергии Гиббса или энергии Гельмгольца.
Подобным же образом к увеличению поверхностной энергии Гельмгольца приводит и работа разрыва связей при дроблении твердых тел (V = const), сопровождающаяся увеличением площади поверхности раздела фаз.
Коэффициент пропорциональности s равен работе увеличения поверхности при постоянных температуре, объеме и составе, отнесенной к единице поверхности. Он численно равен удельной поверхностной энергии Гельмгольца и называется поверхностным натяжением. В случае двух конденсированных фаз чаще используется понятие «межфазное натяжение». Сложилось так из-за того, что это понятие было введено раньше, чем была развита термодинамика поверхностных явлений. Величину s рассматривали как силу, направленную тангенциально к поверхности и стягивающую ее, однако использование такого понятия может привести к неправильному выводу о том, что существует особая, отличная от межмолекулярных сила (поверхностная) и увеличение поверхности есть результат ее растяжения, т.е. увеличения расстояния между молекулами в поверхностном слое. Размерность величины s – энергия на единицу поверхности (джоуль на квадратный метр), или, что то же, сила на единицу длины (ньютон на метр).
12.2. Поверхностные явления в дисперсных системах
В гетерогенных системах, в которых одна из фаз представляет собой сравнительно крупные частицы, поверхность раздела фаз невелика. В таких системах поверхностные явления практически не проявляются. По мере уменьшения размеров частиц (диспергирования) вещества одной из фаз возрастает абсолютная величина поверхности раздела и поверхностные свойства в дисперсных системах приобретают все большее значение.
Мерой раздробленности, или дисперсности, системы принято считать дисперсность D – величину, обратную величине размера (диаметра) дисперсной частицы а.
Для сравнения поверхностей раздела принято пользоваться понятием удельной поверхности S уд., т.е. величиной поверхности всех частиц, заключенной в единицах массы вещества.
Величина удельной поверхности пропорциональна дисперсности системы (обратно пропорциональна размеру частиц):
, (12.2)
где k 1, k 2 и k – коэффициенты пропорциональности, связанные с формой частиц. Например, для частиц шарообразной формы k 1 = p; k 2 = p/6 и k = 6, а для кубической – соответственно 6,1 и 6. При размерах частиц порядка 10 нм величина удельной поверхности – сотни квадратных метров на грамм. Таким образом, в результате диспергирования вещества происходит увеличение роли поверхностных свойств в общих свойствах системы и одновременно увеличивается абсолютное значение поверхностной энергии, что определяет огромное значение поверхностных явлений для дисперсных систем. Поверхностные явления, например, лежат в основе свойств коллоидных систем.
12.3. Поверхностное натяжение и природа вещества
Поскольку поверхностное натяжение является результатом нескомпенсированности межмолекулярного взаимодействия в разных фазах, оно определяется разностью интенсивности взаимодействия молекул внутри каждой фазы и взаимодействия молекул различных фаз. Интенсивность молекулярных взаимодействий внутри фазы в теории поверхностных явлений обычно обозначают термином «полярность». Полярность вещества в очень большой степени связана с такими параметрами, как дипольный момент молекул, диэлектрическая проницаемость, поляризуемость молекул, способность к образованию водородной связи между молекулами. Однако существенное значение играют также плотность вещества, геометрия строения молекул, ориентация молекул в поверхностном слое, определяющая направление силовых полей, возможная взаимная растворимость граничащих фаз, их химическое взаимодействие.
Экспериментальные методы определения поверхностного натяжения применимы к двухфазным системам с легкоподвижной, обратимо изменяемой поверхностью раздела газа с жидкостью или двух несмешивающихся жидкостей. Как правило, они основаны на измерении силы, уравновешиваюшей поверхностное натяжение. Прямое определение поверхностной энергии твердых тел невозможно, и величина s для них оценивается лишь косвенно.
Самое малое поверхностное натяжение характерно для сжиженных инертных газов, поскольку симметричные молекулы их обладают ничтожной поляризуемостью. Поверхностное натяжение органических жидкостей возрастает с увеличением их полярности. Вода обладает очень большой величиной поверхностного натяжения по сравнению с другими жидкостями, что связано со склонностью воды к образованию водородных связей.
Еще выше поверхностное натяжение расплавленных солей и металлов, для которых характерна ионная связь, например:
жидкий гелий Т = –270,5 ˚С s ×103, Дж/М2 – 0,30
гексан (20) 9,8
фенол (20) 42,3
вода (20) 72,7
расплав NaCl (810) 113
жидкое железо (1515) 1880
Поверхностная энергия твердых тел, определяемая косвенными методами, оказалась существенно большей, чем в случае жидкостей.
12.4. Термодинамика поверхностных явлений
в однокомпонентных системах
Для однокомпонентной жидкости поверхностное натяжение s численно равно работе внешних сил при обратимом изотермическом увеличении площади поверхности на единицу при постоянном объеме (т.е. увеличению энергии Гельмгольца F). Таким образом, F = s. По уравнению Гиббса-Гельмгольца
. (12.3)
Обозначая полную поверхностную энергию через e, можно переписать уравнение (12.3) для поверхности:
. (12.4)
При повышении температуры кинетическая энергия движущихся молекул увеличивается, поверхностное натяжение при этом уменьшается. При приближении к критической температуре Т кр. плотности сосуществующих фаз (жидкости и пара) сближаются. При достижении Т кр. граница раздела фаз исчезает и поверхностное натяжение становится равным нулю. Для многих веществ экспериментально показано, что в не очень широком температурном интервале уменьшение s с температурой выражается формулой
, (12.5)
где s – константа, а 
– поверхностное натяжение при выбранной начальной температуре. Величина a для разных жидкостей составляет 0,002 ¸ 0,004 К-1.
12.5. Равновесие фаз при искривленной поверхности
раздела. Капиллярность
На практике нередко приходится иметь дело с искривленной поверхностью раздела. Например, поверхность капли выпукла, а поверхность жидкости в смачиваемом капилляре вогнута.
Понятно, что молекула жидкости, находящаяся на выпуклой поверхности, будет испытывать равнодействующую силу, направленную в глубь жидкости, меньшую, чем на плоской поверхности. На вогнутой поверхности, наоборот, эта сила больше. Поэтому, если на плоской поверхности давление в обеих сосуществующих фазах одинаково, то на искривленной поверхности в условиях равновесия возникает добавочное давление, направленное в сторону той фазы, по отношению к которой поверхность вогнута. Другими словами, при равновесии давление в фазе, отделенной от другой фазы вогнутой поверхности, больше. Эта разность давлений, возникающая по обе стороны искривленной поверхности жидкости, носит название капиллярного (или лапласова) давления.
Величина капиллярного давления зависит от кривизны поверхности и поверхностного натяжения и выражается уравнением Лапласа.
Рассмотрим элементарный участок искривленной поверхности с площадью
S = l1 × l2. (12.6)
Если r 1 и r 2 – радиусы кривизны криволинейных отрезков l1 и l2, то площадь S равна
S = l1 × l2 = r1 j1× r2j2, (12.7)
где j1 и j2 – соответствующие центральные углы (рис. 12.1).
Рис. 12.1. Элементарный участок искривленной поверхности
Если под действием, вызванным разностью давлений D Р по обе стороны поверхности, сама поверхность сместилась на величину dr без изменения кривизны, то произошло увеличение этой поверхности на величину dS. Затраченная работа dW может быть вычислена двумя способами: работа dW равна произведению силы на путь:
dW = DРSdr, (12.8)
но эта же работа dW равна произведению поверхностного натяжения на прирост поверхности:
dW = s×dS. (12.9)
Поэтому
s×dS = DРSdr = j1j2r1 r2DРdr. (12.10)
Найдем dS:
dS = j1j2 (r1 +dr)(r2 +dr) - j1j2r1 r2. (12.11)
После несложных преобразований, пренебрегая членом (dr)2 как величиной бесконечно малой второго порядка, получим:
dS = j1j2r1 dr - j1j2 r2dr. (12.12)
Подставим уравнение (12.12) в уравнение (12.11) и разделим обе части уравнения на r 1 r 2j1j2 , получим формулу Лапласа, выражающую избыток давления со стороны вогнутой поверхности:
. (12.13)
Если поверхность сферическая, то r 1 = r 2 и лапласово давление равно
. (12.14)
Вследствие существования лапласова давления величина давления насыщенного пара жидкости при данной температуре зависит от формы поверхности.
12.6. Уравнение Томсона
Обозначим через r радиус сферической поверхности раздела фаз (радиус капли), через Р 0 – давление насыщеного пара над плоской (r = ¥), а через Р – над выпуклой поверхностью. Перенесем некоторое количество жидкости dm с плоской поверхности жидкости в каплю радиуса r путем обратимого изотермического испарения при давлении Р 0, обратимого сжатия пара от Р 0 до Р и последующей обратимой изотермической конденсации при Р. Поскольку работа испарения и конденсации равны и противоположны по знаку, то общая работа переноса dW, совершаемая над системой, оказывается работой сжатия пара:
, (12.15)
где М – молярная масса вещества.
С другой стороны, в результате переноса dm вещества увеличивается масса капли за счет увеличения ее радиуса на dr и поверхность на dS, что требует затраты энергии на работу против сил поверхностного натяжения (работу увеличения поверхности).
В обоих случаях осуществляется перенос количества dm, поэтому работы dW1 и dW2 равны по абсолютной величине и противоположны по знаку:
. (12.16)
Так как m капли с радиусом r равна m = 4/3pr3r, где r - плотность жидкости - то dm = 4prr2dr. Поверхность капли S = 4pr2, поэтому dS = 8prdr. Подставим эти значения dm и dS в уравнение (12.16) и решим его относительно r. Получим:
(12.17)
(V– молярный объем жидкости 
), что являет собой уравнение Томсона для выпуклой поверхности.
Для вогнутой поверхности кривизна отрицательна. Поэтому:
. (12.18)
Уравнение Томсона (Кельвина) и уравнение Лапласа являются основными уравнениями физической химии поверхностных явлений.
Следствия из полученных уравнений.
Давление пара (насыщенного) жидкости Р 0 над плоской поверхностью (поверхность с r = ¥) меньше, чем давление пара над каплей радиуса r (Р 0 < Р), но больше, чем давление пара Р над вогнутой поверхностью (r < 0, Р 0 > Р).
Чем меньше размер капли, тем больше равновесное давление ее насыщенного пара, и, следовательно, тем выше значение химического потенциала жидкости, т.е. тем не менее устойчиво ее состояние. Поэтому мелкие капли, обладая большим давлением пара, испаряются быстрее. Испарившееся вещество может конденсироваться на поверхности более крупных частиц и на плоской поверхности. Такой процесс роста крупных частиц за счет исчезновения (испарения) мелких носит название изотермической перегонки (переконденсации). Таким образом, всякая полидисперсная система термодинамически неравновесна, а поэтому неустойчива.
Равновесие твердых частиц по отношению к жидкому раствору можно выразить уравнением, сходным с уравнением Томсона. В растворе мерой интенсивности перехода вещества в другую фазу является концентрация насыщенного раствора, и тогда применительно к дисперсной системе твердая фаза – раствор можно записать:
, (12.19)
где С 0 – концентрация насыщенного раствора, С – концентрация вещества в растворе, равновесном с кристалликами размером r. Поэтому при растворении высокодисперсных веществ можно получить концентрацию раствора выше обычной растворимости.
Термодинамическая неравновесность таких систем обуславливает перекристаллизацию вещества – рост крупных кристаллов в пересыщенном растворе за счет растворения мелких. Например, для BaSO4 найдено, что растворимость частиц с размером r = 2 мкм равна 15,3 m моль/л, а растворимость частиц с размером r = 0,3 мкм равна 18,2 m моль/л. При подстановке этих данных в уравнение (12.19) найдем для величины tт-ж = 1250×10-3Дж/ m 2.
Повышение давления насыщенного пара над высокодисперсными частицами по сравнению с частицами крупных размеров обуславливает и некоторое понижение температуры их плавления. Например, уменьшение размера частиц салола до 8 мкм понижает его температуру плавления с 42 °С до 38 °С.
12.7. Капиллярные явления
Особенности условий равновесия на искривленных поверхностях лежат в основе так называемых капиллярных явлений. Если поверхность раздела фаз подвижна (поверхность жидкость-газ или жидкость-жидкость), ее форма изменяется под влиянием поверхностного натяжения, стремясь к форме, отвечающей минимальной поверхности. При смачивании жидкостью стенок капилляра в нем образуется вогнутый мениск, и уменьшение давления под ним компенсируется подъемом жидкости в капилляре (всасывание). При несмачивании образуется выпуклый мениск, и следствием является опускание жидкости в капилляре. С описанным явлением связано также возникновение значительных перенасыщений при образовании новой фазы. Вначале образуются зародышевые частицы весьма малых размеров. Давление пара (или концентрация) раствора, равновесное по отношению к таким высокодисперсным агрегатам (кластерам), заметно выше давления насыщенного пара (концентрации) насыщенного раствора. Таким образом, для образования мелких зародышей необходимо накопление избыточной энергии, т.е. создания пересыщенных состояний, что сильно тормозит образование новой фазы. Теория кинетики зародышеобразования представляет собой одну из важных задач современной физической химии.
Лекция 13.
Адсорбция
13.1. Уравнение адсорбции Гиббса
Строгое определение понятия адсорбции по Дж. Гиббсу: адсорбцией данного компонента на границе раздела двух фаз называется разность между фактическим количеством этого компонента в системе и тем его количеством, которое было бы в системе, если бы концентрации в обеих сосуществующих фазах были постоянны вплоть до некоторой геометрической поверхности, разделяющей их.
Эта разность может быть положительной или отрицательной. Она обозначается символом G (гамма) и имеет размерность моль/м2. Эту величину называют избыточной адсорбцией по Дж. Гиббсу.
Хотя в приведенном определении адсорбция отнесена к геометрической поверхности, не имеющей толщины (что удобно при выводе уравнений), фактически граница между фазами представляет собой очень тонкий слой (поверхностный слой), в котором все свойства отличаются от свойств объемных фаз и изменяются не скачкообразно, а непрерывно.
На рис. 13.1 показано возможное изменение концентрации вблизи границы раздела: концентрация компонента может быть как выше концентраций в обеих фазах (1), так и ниже (2) или иметь промежуточное значение. Эта область может рассматриваться как поверхностный слой. Таким образом, изучая границу раздела фаз, нужно рассматривать состояние трех фаз: двух объемных и одной поверхностной.
Рис. 13.1. Изменение концентрации компонентов у границы раздела фаз;
поверхностный слой – mn-m’n’
Уравнение, устанавливающее связь между всеми параметрами процесса адсорбции – величиной поверхностного натяжения s, концентрацией компонента [ C ] в одной из фаз, его адсорбцией Г, было выведено Дж. Гиббсом в 1876 г. Это уравнение является общим термодинамическим уравнением, справедливым для любых составов и природы поверхности раздела фаз.
Рассмотрим систему, состоящую из двух компонентов 1 и 2 и двух фаз a и b, разделенных поверхностью раздела с площадью S. Общее число молей каждого компонента в системе равно n1 o и n2 o. Если считать, что поверхностный слой не имеет толщины, т.е. представляет собой геометрическую поверхность, то обе объемные фазы будут иметь постоянный состав вплоть до этой геометрической поверхности. Обозначим число молей каждого компонента в каждой из этих фаз соответственно через n1a,n1b; n2a,n2b. Так как на поверхности имеет место адсорбция, то, очевидно, n1o ¹ n1a + n1b и n2o ¹ n2a + n2b.
По вышеприведенному определению адсорбция каждого компонента Г1 и Г2, отнесенная к единице площади поверхности, равна
. (13.1)
Чтобы найти Г1 и Г2, напишем уравнение энергии Гиббса для двух фаз a и b в отдельности и для всей системы в целом. В последнем случае, очевидно, нужно включить в уравнение член sdS:
dGa = - Sa dT + VadP + m1dn1a + m2dn2a;
dGa = - Sb dT + VbdP + m1dn1b + m2dn2b;
dGo = - So dT + VodP + sdS + m1dn1o + m2dn2o. (13.2)
Укажем на уравнение Гиббса-Дюгема, которое устанавливает связь между химическими потенциалами:
dG = - S dT + VdP + Smidn1 (P, T – постоянные). (13.3)
Тогда для бинарной системы получим
dG = m1dn1 + m2dn2. (13.4)
Интегрируя это уравнение при постоянных значениях m 1 и m 2, получим
G = m1n1 + m2n2. (13.5)
Следовательно,
dG = m1dn1 + m2dn2 + n1dm1 + n2dm2. (13.6)
Из (13.4) и (13.6) вытекает, что
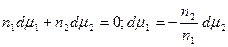. (13.7)
Это уравнение носит название уравнения Гиббса-Дюгема и связывает изменение химических потенциалов компонентов. Тогда с учетом уравнения Гиббса-Дюгема и поверхностных явлений получаем:
n1adm1 + n2adm2 = 0;
n1bdm1 + n2bdm2 = 0; (13.8)
Sds +n1odm1 + n2odm2 = 0.
Сложение двух первых уравнений и вычитание полученной суммы из третьего дает
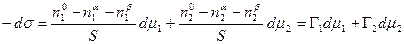. (13.9)
В качестве примера рассмотрим две конкретные системы: двухкомпонентный жидкий раствор, находящийся в равновесии со своим двухкомпонентным насыщенным паром, и твердое тело, находящееся в равновесии с однокомпонентным газом, совершенно не растворимым в этом твердом теле.
Поскольку в первом случае точное положение разделяющей геометрической поверхности несколько условно, то можно выбрать положение ее, при котором
Г1 = 0,
тогда
ds = - Г2dm2. (13.10)
Во втором случае вследствие нерастворимости газа в объеме твердого тела, объемные свойства этого тела, в частности его химический потенциал, не изменяются при адсорбции. Приписывая твердому телу индекс 1, имеем:
m1 = const и dm1 = 0,
поэтому
ds = - Г2dm2. (13.11)
В обоих случаях получено одно и то же уравнение. Поэтому можно считать, что адсорбционное уравнение Гиббса имеет вид:
ds = Г2dm2.(13.12)
Оно является основным в учении о поверхностных явлениях.
Рассмотрим далее реальный раствор. Для реального раствора
m = mо(Т) + Rtlna,
где а – активность, тогда:
dm = RТ d lna.
Подставив это значение в уравнение (13.12), получим:
ds = - Г Rt d lna,
или
. (13.13)
В разбавленных растворах а » С (где С – концентрация)
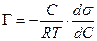, (13.14)
а для идеального или разреженного идеального газа
. (13.15)
Уравнение (13.14) показывает, что если при адсорбции поверхностное натяжение s уменьшается с ростом концентрации С, т.е. ds/dC < 0, то адсорбция Г – положительна. Это соответствует поверхностно-активным веществам. Наоборот, если s растет с ростом С, то ds / dC > 0 и Г – отрицательно. Это соответствует поверхностно-инактивным веществам. Если известна зависимость s от С (т.е. изотерма поверхностного натяжения s = f (C), то по уравнению Гиббса можно для каждого значения концентрации найти ds / dC и по уравнению Гиббса вычислить значение Г, т.е. построить изотерму адсорбции.
13.2. Обзор сорбционных явлений
Адсорбция на границе раздела твердое тело/газ. В общем случае явления, связанные с перераспределением веществ между различными частями гетерогенной системы, называются сорбцией. Сорбция (от лат. sorbeo – сгущать) – это изменение концентрации (часто увеличение) либо у поверхности раздела фаз (адсорбция), либо в объеме одной из фаз (абсорбция). Например, образование раствора за счет поглощения НСl (газа) и поглощение газа металлом (абсорбция). Поверхностная сорбция – адсорбция.
Твердое тело, у поверхности которого происходит адсорбция, называется адсорбентом, адсорбирующийся газ или адсорбирующийся компонент жидкого раствора – адсорбтивом, а адсорбированое вещество – адсорбат.
В строгом определении адсорбции она рассматривается как избыток вещества вблизи поверхности по сравнению с равным объемом вдали от нее. В ряде случаев удобнее рассматривать не избыток, а все количество адсорбата вблизи поверхности. Это количество обозначают символом а и называют полным содержанием, или просто адсорбцией (без указания гиббсова). Так как для пористых твердых тел бывает затруднительно знать величину поверхности, то часто адсорбцию относят не к единице поверхности, а к единице массы (моль/кг или моль/г).
Адсорбция самопроизвольна и протекает при Р = const со снижением энергии Гиббса, а при V = const – со снижением энергии Гельмгольца. Однако при этом происходит не выравнивание концентраций по всему объему системы, а увеличение разности концентраций между газовой фазой (раствором) и поверхностью. Одновременно уменьшается подвижность сорбирующихся молекул. Оба фактора ведут к уменьшению энтропии (D S <0).
По основному уравнению термодинамики находим
DH = TDS + DG (13.16)
Если величины D S и D G – отрицательны, то значение D Н – отрицательно и процесс является экзотермическим.
Важной характеристикой адсорбции является теплота адсорбции. Она является мерой интенсивности адсорбционных сил – сил взаимодействия молекул адсорбата с поверхностью адсорбента и между собой.
Интенсивность взаимодействия адсорбент-адсорбат зависит от состояния адсорбента и от того, какое количество адсорбата уже адсорбировано (от заполнения поверхности). Поэтому различают два основных понятия – интегральная и дифференциальная теплота адсорбции.
Интегральной теплотой адсорбции Q называется полное количество теплоты, выделяющейся при адсорбции n молей адсорбата. Ее относят к единице массы адсорбента (Дж/кг). Дифференциальной теплотой адсорбции q называют отнесенное к 1 молю адсорбата дополнительное количество теплоты, выделяющейся при адсорбции бесконечно малого количества адсорбата:
или 
. (13.17)
Типичные зависимости интегральной и дифференциальной теплоты адсорбции от количества адсорбированного вещества представлены на рисунке 13.2. Прямые 1 для Q и 2 для q соответствуют зависимости Q = ka. Как правило, такая прямая зависимость не наблюдается (она возможна лишь при q = const). Фактически вследствие неоднородности поверхности адсорбента адсорбция происходит сначала на наиболее активных участках поверхности с наибольшим значением дифференциальной теплоты; при больших заполнениях q уменьшается. Это приводит к некоторому замедлению роста Q. Возможен и третий случай. Вследствие взаимного притяжения адсорбированных молекул уменьшается расстояние между ними и дифференциальная теплота адсорбции повышается (кривая 3).
Рис. 13.2. Зависимость интегральной и дифференциальной теплоты адсорбции от количества адсорбированного вещества
13.3. Природа адсорбционного взаимодействия
Величина адсорбции – функция природы адсорбента и адсорбата и зависит от силы взаимодействия между ними. При адсорбции взаимодействуют молекулы, принадлежащие разным фазам, а на границе раздела фаз неизбежно существует асимметрия сил взаимодействия. Кроме того, молекулы адсорбата взаимодействуют не с единичной молекулой адсорбента, а с их совокупностью. Благодаря этому силы взаимодействия в зависимости от их природы могут либо возрастать, либо ослабевать.
Адсорбцию делят на физическую и химическую (хемосорбцию). Как правило, физическая адсорбция обусловлена межмолекулярными (ван-дер-ваальсовыми) силами. В простейшем случае взаимодействие неспецифично, т.е. речь идет об универсальных, дисперсионных силах. Молекулы на поверхности не теряют своей индивидуальности.
Дисперсионное взаимодействие не зависит от температуры. Важным свойством дисперсионных сил является их аддитивность; сила взаимодействия между двумя молекулами не зависит от присутствия других молекул. Аддитивность проявляется в том, что суммируются силы взаимодействия молекул адсорбата со всеми близлежащими атомами поверхности адсорбента. Поэтому при адсорбции пористыми адсорбентами вклад дисперсионных сил в общее взаимодействие оказывается существенно бóльшим. При адсорбции неполярных веществ на полярном адсорбенте (ионный кристалл) к дисперсионным силам притяжения добавляются индукционные силы притяжения диполя, индуцированного электростатическим полем адсорбента. Индукционное притяжение возникает и при адсорбции полярных молекул на неполярном адсорбенте.
Адсорбция полярных молекул на полярном адсорбенте вызывает ориентационное кулоновское взаимодействие диполя адсорбата с электростатическим полем адсорбента. Энергия индукционных, ориентационных и дисперсионных сил при парном взаимодействии обратно пропорциональна шестой степени расстояния между центрами взаимодействующих атомов. Однако ориентационные и индукционные взаимодействия, будучи электростатическими, не являются аддитивными. Так, появление третьей молекулы в поле взаимодействия двух других изменяет ориентацию молекулы и ослабляет эти взаимодействия. Поэтому энергия взаимодействия молекулы адсорбата с поверхностью адсорбента может оказаться меньше, чем энергия ее взаимодействия с одним центром на поверхности. При адсорбции пористыми адсорбентами индукционное и ориентационное взаимодействия вносят меньший вклад. Поэтому наибольшую роль чаще всего играет дисперсионное взаимодействие. Для неполярных или слабополярных молекул его вклад может быть стопроцентным.
Неспецифический характер взаимодействий, вызывающих физическую адсорбцию, определяет и основные признаки этого явления. Равновесие при физической адсорбции устанавливается быстро и обратимо. Теплота физической адсорбции превышает теплоту конденсации обычно не более чем на ~20 кДж/моль.
Химическая адсорбция имеет место, когда молекулы адсорбата вступают в химическое взаимодействие с поверхностью адсорбента с образованием
поверхностных химических соединений, но без образования новой объемной
фазы. Она гораздо более избирательна и чувствительна к химической природе адсорбата и адсорбента. Теплоты хемосорбции обычно велики (100‑200 кДжмоль).
Хемосорбция может протекать довольно медленно, со скоростью, определяемой наличием некоторого активационного барьера. Поэтому ее часто называют «активированная адсорбция». При низких температурах скорость хемосорбции обычно мала. Хемосорбция, как правило, необратима.
Существует большое многообразие форм адсорбции, переходных между физической и химической адсорбцией. Так, например, широко распространенным видом такого переходного взаимодействия является образование водородной связи при адсорбции. Это характерно для адсорбентов, содержащих на поверхности гидроксильные группы (силикагель, алюмогель и др.). Для этого пограничного типа адсорбции теплота составляет обычно 20-40 кДж/моль.
В связи с разнообразием адсорбционных сил единая теория адсорбции, позволяющая на основе предположений о механизме процесса составить общее математическое описание, пока отсутствует.
13.4. Термическое уравнение адсорбции.
Изотерма адсорбции
Для данной пары адсорбент – адсорбат величина адсорбции а или Г определяется двумя основными термодинамическими параметрами состояния: температурой Т и давлением Р для газообразного состояния адсорбата или Т и концентрацией С при адсорбции из растворов. Все три величины связаны функциональной зависимостью, называемой термическим уравнением обратимой сорбции: