Введение
Если в точных науках, например в физике, математические методы давно уже стали их неотъемлемой частью, то при изучении биологии и смежных с ней наук математические методы и физические законы используются еще недостаточно. Отсутствие интереса к математике со стороны биологов в прошлом частично оправдывалось традиционно качественным подходом к изучению биологических проблем и медленным развитием наших представлений о степени сложности живых систем. Можно надеяться, однако, что в самом недалеком будущем биологическая подготовка всех студентов будет непременно включать курс математического анализа, элементы которого, возможно, будут освоены еще в средней школе. Тогда будет значительно легче устанавливать связь между различными дисциплинами и во всех средних и высших учебных заведениях курс общей биологии будут слушать студенты, уже вооруженные знаниями по физической химии. Но пока на это рассчитывать не приходится.
Льюис определял предмет физической химии как изучение того, что в науке наиболее интересно (сам он был физико-химиком). Надеясь на должное понимание этой точки зрения, мы начнем наше изложение с вопроса о различных типах физических законов. Поскольку физическая химия, а вместе с ней и биохимия могут рассматриваться как приложение законов физики к химическим и биохимическим системам, такое начало логически вполне себя оправдывает.
Один из законов физики известен почти каждому – это закон сохранения энергии. Его иногда называют основным законом природы, поскольку он вытекает не только из научного, но и из всего человеческого опыта. Многие философы, пытавшиеся отыскать метафизический смысл этого закона, в целом находили его достаточно надежным. Для всех неядерных реакций закон сохранения энергии, насколько мы знаем, остается справедливым в пределах ошибок эксперимента; пока не обнаружено ни одного исключения из него. Закон выполняется независимо от того, сколько молекул, частиц или компонентов содержит изучаемая система. Вместе с тем некоторые физические законы называют «статистическими» – они формулируются только по отношению к событиям, повторяющимся достаточно много раз. Законы этого типа легче всего проиллюстрировать известным примером с подбрасыванием монеты. Подбрасывая монету, мы можем быть уверены, что «орел» или «решка» выпадут в соотношении 50 : 50 только в том случае, если у нас хватит терпения подбрасывать ее достаточно много раз. Если мы 500 раз подбросим десять монет, то, согласно теории вероятности, одна «решка» и 9 «орлов» выпадут примерно в 10% случаев, а 5 «решек» и 5 «орлов» с наибольшей вероятностью выпадут 123 раза на 500 попыток. Такого типа вероятностные законы встречаются и в физике. Один из наиболее важных физических законов, толкования которого приносят философам немало беспокойства, гласит: все встречающиеся в природе системы с течением времени стремятся к наиболее неупорядоченному состоянию – как говорится, все в конце концов скатывается вниз. Такой закон, как и в случае с монетой, при малом числе событий может и не выполняться.
|
|
Вы можете заметить, что почти все физические законы сопровождаются довольно строгим указанием условий, в пределах которых они выполняются. Условия эти чаще всего выглядят вполне логично и естественно. Можно сослаться, например, на законы химического равновесия, согласно которым состояние равновесия зависит от температуры. Кроме того, в физической химии и биохимии часто оказывается выгодно упростить математическую формулировку некоторых общих законов; их применимость в результате заметно сужается, но зато неизмеримо возрастает их польза. Например, наиболее полезные уравнения, описывающие свойства растворенных веществ и их взаимодействие с растворителем, представляют собой упрощенный вариант общих уравнений, применимых лишь к случаю разбавленных растворов. В уравнениях, выражающих поведение разбавленных водных систем, мы можем заменять молярность на моляльность, подставлять молярные доли вместо молярности и делать многие другие удобные упрощения. Упрощенные законы часто называют «предельными законами». Впрочем, если подойти строго, то почти все физические законы являются «предельными», поскольку всем им присущи какие-то пределы применимости. Однако в последующем изложении под «предельными законами» мы будем подразумевать лишь те, которые возникают в результате достаточно радикальной математической хирургии.
|
|
Физические законы выводятся двумя способами: из экспериментальных наблюдений и в результате математического выражения неких основополагающих принципов. Теоретические выводы фундаментальных законов должны опираться на обобщения, вытекающие из экспериментальных наблюдений. В основе всех этих выводов лежит единый принцип строго научного подхода – научный метод, который проложил науке дорогу сквозь все невзгоды средневековья и придал ей нужную строгость и объективность.
|
|
Научный метод составляет самое существо современной науки, без него было бы невозможно существование науки и техники наших дней. Попробуем теперь чуть ближе взглянуть на этот важный во всех отношениях метод, на его возможности, требования и запреты. Тот, кого мы называем ученым, должен иметь определенный талант и быть готовым использовать научный метод – он должен уметь наблюдать, стремиться к анализу окружающих явлений и к объективной и честной оценке смысла своих наблюдений. На этом основаны все научные построения.
Вначале, наблюдая за поведением некоторой системы, ученый замечает, что при определенных условиях эта система ведет себя воспроизводимым образом; в результате у него появляется возможность предсказывать ее поведение. Тогда ученый, как правило, описывает поведение системы неким математическим уравнением, которое мы называем эмпирическим.
Любопытство ученого этим не удовлетворяется, и он задает вопрос: не связано ли наблюдаемое поведение системы с каким-либо фундаментальным свойством материи? В поисках ответа ему приходится сформулировать вопрос несколько иначе: нельзя ли придумать такую совокупность основных свойств материи, которая находилась бы в согласии с наблюдаемым поведением системы? Предположение о тех или иных свойствах материи именуются гипотезой.
Гипотезы подкрепляются определенной аргументацией и облекаются в соответствующую математическую форму. В конечном итоге выводится уравнение, позволяющее предсказывать поведение системы. Это уравнение сопоставляется с исходным эмпирическим уравнением, выведенным из непосредственных наблюдений. Теперь ученый должен проверить, в какой мере его общие построения согласуются с наблюдаемыми явлениями, так как научный метод исходит из того, что проникновение в фундаментальные свойства материи возможно лишь постольку, поскольку теоретические предсказания согласуются с экспериментальными наблюдениями.
Практически во всех случаях теоретические выводы ведут к постановке новых экспериментов, которые могут служить дальнейшей проверкой исходных предположений. Обычно ученый убеждается в том, что предсказываемое поведение материи несколько расходится с экспериментальными результатами, и ему приходится либо каким-то образом уточнять и усложнять прежние гипотезы, либо развивать совершенно новые идеи и представления. Процесс постановки новых экспериментов и уточнения основных понятий продолжается до тех пор, пока не наступит момент, когда дальнейшее усложнение теории в рамках имеющихся экспериментальных данных уже не дает никаких ощутимых выгод.
Следует указать, что иногда в предсказании поведения системы в равной степени полезными могут оказаться совершенно различные постулаты. Такую ситуацию иллюстрирует, например, случай, когда две разные теории привели нас к представлению о «двойственной природе» энергии излучения. Ученые не всегда настаивают на том, чтобы полезная система постулатов обязательно была единственно возможной; когда приемлемые черты обнаруживаются сразу у нескольких систем постулатов, то стремятся извлечь пользу из каждой.
Ученый постоянно стремится использовать доступный ему метод для развития сразу всех мыслимых объяснений одного и того же явления, однако истинным является, вероятно, лишь одно из них. Примеры, когда приходится прибегать сразу к двум или нескольким системам постулатов, говорят о том, что каждая из них содержит долю истины. По мере развития науки всегда появляется единая диалектическая по своей природе система представлений, поддающаяся математической интерпретации, способная выдержать все виды аргументации и подкрепленная экспериментальными доказательствами.
По мнению авторов, студенты, посвятившие себя науке, всегда должны проявлять интерес к возможному применению научных идей и представлений в других сферах человеческой деятельности – в экономике, политике, социологии. Мы вовсе не утверждаем здесь, что научный метод применим и к отношениям между людьми, однако мы уверены: в тех случаях, когда приходится выбирать правильное решение, нельзя обойтись без принципов, лежащих в его основе.
Лекция 1.
Газовые законы
1.1. Температура и нулевой закон термодинамики
Изучение физической химии часто начинают с законов поведения газов. Связано это с тем, что законы поведения газов представляют собой основу для понимания поведения более сложных систем, поскольку в той или иной мере, с определенными допущениями, все системы могут быть мысленно или экспериментально упрощены. Такое упрощение часто называют моделированием определенных свойств сложной системы. Поведение газов относительно просто по двум причинам:
1. Смеси газов всегда образуют однородные по составу, истинные растворы, находящиеся в одной «фазе».
2. При одной и той же температуре и одном и том же давлении одинаковые объемы газов содержат одинаковое количество молекул (это известный закон Авогадро).
Системы газов характеризуются общими параметрами – такими, как масса, объем, температура, давление, плотность и др. Некоторые параметры связаны между собой. Это означает, что если мы, например, знаем массу и объем газа, то нам не представляет труда вычислить его плотность, так как
плотность = масса/объем.
Напомним, что, рассматривая свойства газов, мы пренебрегаем влиянием внешних полей. Экспериментаторы стремятся обойтись минимальным числом параметров (свойств), так как их непосредственное измерение резко увеличивает трудозатраты на эксперимент.
По-видимому, не следует объяснять, что подразумевается под такими свойствами, как масса, объем, плотность, давление. Наиболее трудно воспринимается понятие температуры. То, что мы обычно понимаем под температурой, есть не что иное, как мера средней кинетической энергии молекул некоего тела. Если рассматривать перенос тепла от одного тела к другому, то это представляет собой просто передачу кинетической энергии молекул одного тела другому. Однако такие понятия температуры и тепла были приняты далеко не сразу. Вы помните, что ранее тепло рассматривалось как некая невидимая «калорическая» жидкость – теплород, которая перетекает от одного тела к другому. Забегая вперед, укажем, что состояние газа обусловлено любыми двумя из трех его свойств: P, V, T. Иначе говоря, из трех переменных независимыми являются только две. Математически мы можем записать это в форме
T = f (P,V) (эмпирическая температура). (1.1)
Определение температуры, которое следует из выражения 1.1, часто называют нулевым законом термодинамики. Нулевой закон термодинамики часто выражают через понятие температуры и теплового равновесия: две системы, находящиеся в тепловом равновесии с третьей, находятся в тепловом равновесии друг с другом.
Допустим, что два тела, нагретые до разных температур, приводятся в контакт друг с другом до наступления равновесия.
Это значит, что
f(P1,V1) = f(P2,V2) или T1= T2. (1.2)
На практике это означает, что одно тело может быть использовано для определения температуры другого тела. Это легко видеть из уравнения. Допустим, у нас сохраняется одинаковым давление для двух тел, т.е. Р1= Р2, тогда после установления равновесия по изменению объема можно судить о температуре анализируемого образца. На этом принципе работают известные нам термометры. Для этого берется любое тело или жидкость, которые линейно расширяются с температурой, их калибруют, выбирая удобную шкалу. В повседневной практике обычно используют стоградусную шкалу Цельсия, в которой за ноль принимается температура плавления льда, а за 100 °С – температура кипения воды. Все это при атмосферном давлении.
1.2. Законы поведения идеальных газов:
уравнение состояния идеального газа
Два очень важных закона, известных как закон Бойля и закон Шарля, были открыты экспериментально. Их называют эмпирическими законами. Так, в 1662 году Р. Бойль измеряет степень сжатия атмосферного воздуха в U‑образной трубке, короткий конец которой был прокалиброван и запаян. В длинный конец можно было добавлять ртуть. Высота воздушного столба А была пропорциональна объему. Оказалось, что произведение Р´А было приблизительно постоянным. Р – высота ртутного столба. Из этого был сделан вывод, что при неизменной температуре
P1V1= P2V2.(1.3)
Это и есть закон Бойля.
Закон Шарля (он одновременно был открыт Ж.Л. Гей-Люссаком) тоже был найден эмпирически. Сегодня он гласит:
В процессе охлаждения газа при постоянном давлении на каждый градус Цельсия его объем уменьшается на 1/273,15 того объема, который он занимает при 0 °С.
Математически это можно записать уравнением
(при постоянном давлении). (1.4)
Чем интересно это уравнение? Оно указывает, что при t = -273,15 °С газ вообще должен исчезать, т.е. не занимать никакого объема. Это невероятно. Понятно, что это уравнение не может выполняться точно. Тем не менее температура -273,15 °С получила название абсолютного нуля. Абсолютный ноль использован в качестве точки отсчета в шкале Кельвина (или абсолютной шкале).
Приведенное выше уравнение можно записать так:
, где T = t + 273,15. (1.5)
При объединении законов Бойля и Шарля мы получим уравнение, которое позволяет характеризовать поведение газа при изменении всех трех параметров – температуры, давления, объема.
Рис. 1.1. PV-изотермы идеального газа
Точка P0V0 находится на изотерме (так называется кривая, полученная при одной и той же температуре), отвечающей 0 °С (рис. 1.1). В этой точке давление равно 1атм, а объем для газа равен 22,414 л. Этот объем при нормальных условиях (0 °С, 1 атм.) занимает 1 моль газа. Если двигаться по изобаре (т.е. по линии, соответствующей одному и тому же давлению), то эта траектория описывается уравнением Шарля
.
Умножим обе части уравнения на Р 0
.
Но по закону Бойля
VТРо=Р V,
тогда
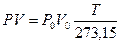(при постоянной температуре),
т.е. если двигаться по изотерме.
Сейчас обозначим 273,15 как Т0 и получим хорошо известное уравнение, объединяющее уравнение Бойля и Шарля:
. (1.6)
Как мы уже видели, 
представляет собой постоянную величину, которая является коэффициентом пропорциональности, переводящим градусы абсолютной шкалы в единицы энергии. Действительно, PV имеет размерность энергии. Полученный коэффициент обозначают величиной R, и он носит название универсальной газовой постоянной. В результате мы получим уравнение идеального газа или уравнение Менделеева-Клайперона:
Р 
= RТ (для 1 моля газа, где молярный объем), (1.7)
PV = nRT (для n молей газа). (1.8)
Название этого уравнения уже говорит о том, что оно верно для идеального газа и, наоборот, газ является идеальным, когда точно подчиняется этому уравнению. В реальном газе необходимо учитывать, что сами его молекулы занимают определенный объем. Кроме того, между молекулами газа имеются силы притяжения.
Рассмотрим первую часть уравнения. PV имеет размерность энергии. Действительно, допустим, что давление выражено в дин/см2, а объем в см3. Произведение PV имеет размерность дин/см, а это есть не что иное, как эрг, т.е. единица энергии в системе СГС (сантиметр/грамм/секунда). Аналогично PV можно выразить в Дж (система СИ)
В принципе энергию в любой форме можно представить в виде двух множителей: один из них будет фактором интенсивности, а другой – емкости.
Например, для уравнения идеального газа фактор интенсивности – это давление, а емкости – объем; в выражении кинетической энергии фактором емкости является масса, а половина квадрата скорости – интенсивность. В случае электрической энергии фактор емкости – это заряд, а фактор интенсивности – потенциал.
В принципе различные формы энергии легко можно переводить один в другой. Однако необходимо помнить, что ни в коем случае не допускается приравнивание друг к другу отдельных сомножителей, т.е. отдельно факторов интенсивности или факторов емкости.
Для того, чтобы отличать факторы емкости и факторы интенсивности, полезно помнить, что фактор интенсивности не зависит от размеров и протяженности системы.
Хотелось бы сказать, что коэффициент пропорциональности (R) очень удобен для перехода от одного типа энергии к другому. Более подробно мы с этим познакомимся на практических занятиях.
Здесь же укажем, что
R = 8,314 107 эрг/моль × град;
R = 8,314 Дж/моль×град;
R = 1,987 кал/моль×град.
Газовая постоянная тесно связана с теплоемкостью газов. Теплоемкость – это количество тепла, необходимое для повышения температуры вещества на 1°. Обычно речь идет о молярной теплоемкости, т.е. она относится к количеству вещества в один моль. Удельная теплоемкость относится к одному грамму, т.е. это количество тепла, необходимого для нагрева 1 г вещества на 1°. Количество тепла, необходимого для нагрева вещества, зависит не только от его массы, но и от условий нагрева. Поэтому различают молярную теплоемкость при постоянном объеме 
и при постоянном давлении 
. Для жидкостей и твердых тел и практически одинаковы. Для газа больше на то количество тепла, которое затрачивается на расширение газа. Для одноатомных газов » 5 ккал/град, а » 1 кал/град. ` – = 2 кал/град » R. Для многоатомных такая зависимость не сохраняется. Обусловлено это тем, что подводимая энергия переходит не только в поступательную, но и в колебательную и вращательную энергию.
1.3. Кинетическое уравнение газов
Мы подчеркивали, что законы Бойля и Шарля получены эмпирическим, опытным путем. Однако эти уравнения могут быть выведены и теоретически. Еще в 1738 году Бернулли теоретическим путем пришел к закону Бойля, рассматривая процесс столкновения молекул газа со стенками сосуда. Совокупность представлений о температуре и давлении газов как проявление движения молекул называют кинетической теорией газов.
В этом случае давление рассматривается как результат бомбардировки молекулами стенок сосуда, а температура считается пропорциональной средней энергии поступательного движения молекул.
Для вывода уравнения необходимо ввести ряд упрощений.
1. Молекулы пренебрежимо малы по сравнению с разделяющими их расстояниями.
2. Отсутствует взаимодействие между молекулами.
3. Молекулы движутся по прямым линиям и испытывают идеально упругие столкновения друг с другом и со стенками сосуда.
Это означает, что при столкновении молекул их средняя кинетическая энергия сохраняется до тех пор, пока температура остается постоянной. Эти условия практически соблюдаются в случае малых плотностей газа.
Рассмотрим простую систему из N молекул газа, каждая из которых имеет массу m. Температура системы Т. Молекулы находятся в коробке кубической формы с ребром, равным а. Молекулы двигаются со скоростями v1, v2, v3... vN. Понятно, что молекулы могут двигаться в разных направлениях. Это можно представить как движение в системе координат x, y, z, совпадающих с ребрами куба. Для молекул эти скорости будут vx1, vx2, vx3... vxN; Vy1, vy2, vy3... vyN; vz1, vz2, vz3... vzN:
V12 = Vx1 2 + Vy12 + Vz12;
V22 = Vx2 2 + Vy22 + Vz22;
V32 = vx3 2 + vy32 + vz32;
vN2 = vxN 2 + vyN2 + vzN2.
Cреднеквадратичная скорость молекул будет равна:
. (1.9)
C одной и той же стенкой молекула будет сталкиваться через каждые 2 а. Если ее скорость вдоль оси х равна vx см/сек, то она будет ударять об эту стенку vx /2 а раз в секунду. После каждого столкновения молекула будет отскакивать с такой же скоростью vx, не теряя кинетической энергии. Кинетический момент (импульс) молекулы равен произведению массы на скорость, а скорость изменения импульса во времени есть не что иное, как сила.
Действительно, основное уравнение механики f = ma, где а – ускорение. Ускорение равно изменению скорости во времени dv/dt, тогда сила равна mdv/dt или f = d(mv)/dt.
Импульс молекулы до столкновения был mvx, а после стал -mvx. Изменение импульса одного столкновения равно 2 mvx. Молекула сталкивается со стенкой vx/2а раз в секунду. Тогда
. (1.10)
Полная сила, действующая на стенку со стороны всех N молекул, равна сумме сил, действующих со стороны каждой отдельной молекулы:
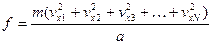, (1.11)
а давление – это сила, действующая на единицу площади, т.е. на а2, тогда
, (1.12)
но а3 равно объему куба;
. (1.13)
То же самое можно написать для других осей.
После группировки получим:
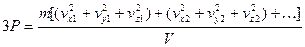. (1.14)
Принимая во внимание уравнение для квадратичной скорости, получим:
или 
(1.15)
или
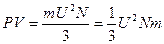, (1.16)
где N – число молекул в сосуде, а U – среднеквадратичная скорость молекул.
Поскольку N и m – постоянны, а скорость молекулы является функцией лишь температуры, то понятно, что
. (1.17)
Любые виды энергии легко переводятся друг в друга с использованием газовой постоянной R и числа молей газа, следовательно
PV = nRT.
1.4. Уравнение состояния реальных (неидеальных) газов.
Уравнение Ван-дер-Ваальса
Речь уже шла о том, что свойства реальных газов редко полностью могут быть описаны законами, выведенными для идеальных газов. Это особенно касается состояний при высоких давлениях и низких температурах. В этих условиях объем системы становится относительно малым и необходимо учитывать собственный объем молекул. Кроме того, начинают действовать силы межмолекулярного притяжения. Для идеального газа произведение PV является постоянным.
Рис. 1.2 показывает, что поведение О2, Н2 и CO2 отклоняется от поведения идеального газа. Причем вид отклонения зависит от природы газа.
Рис. 1.2. Отклонение в поведении реальных газов от идеального в условиях высоких давлений
Чтобы как-то устранить причины, из-за которых уравнение идеального газа практически неприменимо для описания поведения реальных газов, Ван-дер-Ваальс в 1879 году предложил включить в него два дополнительных члена – а и b: константу а добавляют к Р для того, чтобы учесть (скомпенсировать) уменьшение давления из-за межмолекулярного притяжения; константа b учитывает эффективный объем молекул газа, и она вычитается из . Обе константы подбирались эмпирически. В результате для одного моля газа уравнение приобретает вид:
. (1.18)
Однако в этом уравнении появились еще некоторые члены. Так, поправка к давлению принята равной 
по той причине, что молекулы на поверхности газа притягиваются не только друг к другу (к молекулам на поверхности), но и к молекулам, находящимся внутри. Сила притяжения зависит от плотности газа как на поверхности, так и внутри. Поскольку плотность – это масса/V, то ее влияние можно учесть умножением константы а на 1/V2. Поправка b в реальном случае примерно в 4 раза превышает собственный объем молекул моля газа. Ее иногда называют исключенным объемом, так как она соответствует пространству, реально исключаемому одним молем плотно упакованных молекул. Поправки а и b для любого газа приводятся в расчете на 1 моль. Если количество газа больше или меньше одного моля, необходимо пользоваться следующим уравнением
. (1.19)
В практике при расчетах обычно используются табличные данные по значениям а и b.
Это важно в некоторых случаях при расчетах метаболических процессов, в результате которых выделяется, например, СО2.
Однако в большинстве случаев при метаболических процессах давление выделившегося газа относительно невелико. Поэтому ошибка при использовании уравнения, применимого к идеальному газу, для расчетов поведения реальных газов находится в пределах 1-2%. Это меньше, чем стандартная ошибка большинства экспериментов, и поэтому в обычных условиях уравнение Ван-дер-Ваальса используется редко.
1.5. Закон парциальных давлений Дальтона
Зато очень часто в практике необходимо использование закона Дальтона, или закона парциальных давлений. Он основан на том, что в смеси газов каждый газ оказывает такое же давление, какое он оказывал бы, если бы в сосуде присутствовал один.
Давление компонентов газовой смеси зависит только от числа молей каждого из них, так как температура и объем для всех газов в смеси одинаковы.
Давление каждого из газов называют парциальным давлением. Согласно закону парциальных давлений Дальтона, общее давление газовой смеси равно сумме парциальных давлений:
Pобщ= P1+ P2+ P3+... + PN. (1.20)
Если V – общий объем, а n1, n2, n3 и т.д. – число молей каждого компонента, то
PV=n1RT+n2RT+n3RT+...+nNRT=RT(n1+n2+n3+...+nN). (1.21)
Парциальное давление одного из газов, допустим 1, будет равно
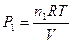. (1.22)
Понятно, что отношение парциального давления газа к его общему давлению равно отношению числа молей этого компонента к числу молей всех газов в смеси:
. (1.23)
Это отношение называют молярной долей и обозначают символом Х. Для газа 1 молярная доля равна Х1 и т.д. Парциальное давление учитывается во многих расчетах. Например, операции по измерению объемов, включающих сбор газов над поверхностью воды, требуют учета парциального давления паров воды в газовой смеси. По сравнению с водяными парами пары ртути имеют значительно более низкое давление, и это создает ощутимые преимущества при использовании ртути в качестве вытесняемой жидкости, так как парциальным давлением паров ртути в таких расчетах вполне можно пренебречь.
С другой стороны, хорошо известно, что вдыхаемый нами воздух является смесью газов. Выдыхаемый воздух отражает происходящий в легких процесс газового обмена. Он насыщен парами воды. Парциальное давление водяного пара достаточно заметно и равно приблизительно 48 мм.р.с. Поэтому, если общее давление выдыхаемого воздуха равно 760 мм, то давление, обусловленное смесью газов О2 + СО2 + N2, будет равно не 760, а 760 – 48 = 712 мм.р.с.
Лекция 2.
Первое начало термодинамики и термохимия
2.1. Вводная часть
Термодинамика – это наука о теплоте и ее превращениях. Она возникла в конце восемнадцатого века в результате интереса к повседневно встречающимся процессам превращения работы, теплоты и материи. Первые количественные термодинамические эксперименты были поставлены для выяснения тепла трения, возникающего при сверлении орудийных стволов (Б. Томпсон). В термодинамике наиболее известны такие имена, как Дж. Блэк, А. Лавуазье, Г. Гесс, Л. Карно, Дж. Джоуль, Дж, Максвел, Р. Клаузиус, У. Кельвин, Г. Гельмгольц, Л. Больцман, Я. Вант-Гофф, Дж. Гиббс.
Ранние работы по термодинамике были посвящены описанию количественных соотношений между теплотой и другими формами энергии. В настоящее время в этой области научных исследований наблюдается сдвиг от анализа энергетических изменений, сопровождающих превращения материи, в сторону использования термодинамики в качестве инструмента, необходимого для понимания и предсказания поведения систем в связи с их энергетическими характеристиками.
Особенно важные перемены произошли после создания статистической термодинамики. Статистическая термодинамика имеет дело с поведением самих молекул, а не с макроскопическими системами типа паровых двигателей или такими процессами, как перегонка, кристаллизация, электролиз. В статистической термодинамике сначала изучают отдельные атомы и молекулы, а затем их коллективное поведение. В классической термодинамике изучают только свойства макроскопических тел в целом, а отдельные частицы не рассматривают. Оба подхода очень много дают химику и биохимику, но мы пока ограничимся освоением лишь классических подходов. С помощью термодинамики, или энергетики, как ее иногда называют, есть возможность предсказать максимальную работу, которую можно получить в определенном процессе, определить состояние равновесия, максимально возможный выход, оптимальную температуру и давление для данной реакции, выбрать лучший растворитель. Термодинамика может ответить на вопрос о том, будет ли реакция протекать в нужном направлении. Но термодинамика не может предсказать необходимое для этого время, указать на механизм реакции. Например, используя термодинамику, можно утверждать, что при температуре возгорания бензин способен самопроизвольно реагировать с кислородом, выделяя двуокись углерода, воду, тепло. Эта реакция предпочтительна. Можно вычислить, сколько при сгорании выделилось тепла.
Однако термодинамика не отвечает на вопрос о том, какова величина теплового барьера, который должен быть преодолен для того, чтобы реакция пошла самопроизвольно, т.е. термодинамика изучает в основном конечные, равновесные состояния. Скорости и механизм реакции рассматривают в разделе «Кинетика».
2.2. Некоторые понятия, используемые в термодинамике
Под понятием энергия обычно понимают способность производить работу. Решая какую-либо задачу методами термодинамики, необходимо прежде всего выделить из окружающего мира какую-то систему. Это может быть дождевая капля, двигатель, организм, планета и т.д. Если говорят, что выделенная система гомогенна, это означает, что свойства системы одинаковы во всех частях, и система непрерывна от точки к точке. Если говорят, что система гетерогенна, это означает, что в ней присутствует не менее двух областей, называемых фазами, которые отделены друг от друга поверхностями, называемыми границами раздела. Системы бывают трех типов: открытые, закрытые и изолированные. В закрытой системе во время процесса происходит изменение энергии, но масса остается постоянной. В открытой системе может изменяться как энергия, так и масса. В изолированной системе не происходит обмена с окружающей средой ни массой, ни энергией!
Очень часто в термодинамике сталкиваются с понятием равновесие. Если состав и свойства системы достаточно долго не меняются, то говорят, что система находится в равновесии. Однако химическое равновесие не является состоянием покоя. Это состояние, в котором реакция протекает как в одну, так и в другую сторону, но с одинаковыми скоростями.
Состояние системы определяется ее свойствами. Если изменяется одно из свойств, состояние системы меняется. При изучении системы обычно рассматриваются такие свойства, которые легко измерить. Это, в частности, температура, давление, объем, состав. Некоторые свойства взаимосвязаны, поэтому нет необходимости измерять их все одновременно.
К сожалению, наши знания и возможности не позволяют вычислить (определить) весь запас энергии системы. Поэтому используется сравнительный подход. Часто энергия системы сравнивается с каким-либо стандартом (стандартным состоянием). Например, газ обычно сравнивается с идеальным газом при стандартных условиях, жидкий растворитель – с чистой жидкостью, твердое вещество – с его наиболее стабильной кристаллической формой. Такие состояния, называемые стандартными, представляют собой точки отсчета, относительно которых измеряют изменение в системе.
2.3. Формулировка первого начала термодинамики
Первое начало термодинамики – это закон сохранения энергии. Он впервые четко сформулирован Г. Гельмгольцем в 1847 году. Этот закон не может быть четко доказан, но является результатом всего человеческого опыта. Такие законы часто называют законами природы. Известный математик А. Пуанкаре как-то иронически заметил, что в сущности все твердо верят в закон сохранения энергии потому, что математики принимают его за экспериментальный факт, а экспериментаторы считают его математической теоремой.
Есть несколько формулировок первого закона термодинамики. Если одна из них принимается в качестве основной, то все другие являются следствиями, вытекающими из нее.
Одна из формулировок звучит следующим образом: энергия не создается и не уничтожается. Возможны лишь превращения энергии из одного вида в другой в строго эквивалентных количествах.
Следствием из этого закона является вывод, что невозможен вечный двигатель первого рода, т.е. нельзя создать такой двигатель, который совершил бы работу без затраты энергии. Создание такого двигателя возможно только в том случае, если неверен первый закон.
Часто используется еще одна формулировка первого начала термодинамики: внутренняя энергии изолированной системы есть величина постоянная.
Если данной системе передается некоторое количество энергии в форме тепла Q, которое идет только на приращение внутренней энергии системы DU и на совершение системой работы W, то, согласно первому началу,
Q = DU + W, (2.1)
для бесконечно малых изменений
dQ = dU + dW. (2.2)
Уравнения (2.1) и (2.2) являются математическим выражением первого начала термодинамики.
Укажем, что DU и dU не зависят от пути перехода системы из начального состояния в конечное, т.е. внутренняя энергия является функцией состояния системы.
Справедливость этого утверждения можно доказать следующим образом (рис. 2.1).
Предположим, что в состоянии (I) внутренняя энергия системы U1. Из этого состояния система переходит в состояние (2), в котором ее внутренняя энергия равна U2.
Рис. 2.1. Схематическое отображение путей перехода системы из состояния 1 в состояние 2 и обратно