ax + by = c, (3)
Теорема 3. Линейное диофантово уравнение (3) разрешимо тогда и только тогда, когда оно число d = НОД (a 1, a 2, a 3,…, an) делит число b.
Теорема 4. Пусть a, b, c Î Z, a ¹ 0 или b ¹ 0, d = НОД(a, b). Если (x 0, y 0) решение уравнения
Тогда все решения уравнения (3) находятся по формулам:
, (4)
где t - произвольное целое число. Решение (x 0, y 0) можно найти по формулам
, (5)
где m – длина цепной дроби при разложении числа a/b в цепную дробь, Pm- 1, Qm- 1 – числители и знаменатели соответствующих дробей.
Примеры 7. Решить ДУ 2346 x - 1456 y = 22.
Так как НОД(2346, 1456) = 2 и 2|22, то данное уравнение разрешимо и равносильно уравнению 1173 x - 728 y = 11. Разлагаем дробь 1173/728 в цепную дробь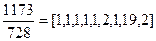 
и находим длину дроби m = 9, и все ее подходящие дроби (см. пример 6). Находим P 8 = 572, Q 8 = 355,
.
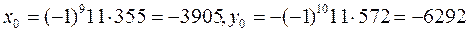Тогда общее решение уравнения имеет вид:
.
Уравнение (3) в частных случаях легко решить методом замены переменных.
Пример 8. Метод замены переменных решить уравнение 34 x - 13 y = 53.
Так как 34 = 13×2 + 8, то уравнение представим в виде
(13×2 + 8) x - 13 y = 53, 8 x + 13(2 x - y) = 53.
Отсюда, полагая z =2 x - y, получим уравнение 8 x + 13 z = 53. Продолжая такие замены переменных, последовательно находим
13 = 8×1+ 5, 8 x + (8×1 + 5) z = 53, 8(x + z) - 5 z = 53, w = x + z, 8 w + 5 z = 53; 8 = 5×1 + 3, (5×1 + 3) w + 5 z = 53, 3 w + 5(w + z)= 53, u = w + z, 3 w + 5 u = 53;
5 = 3×1 + 2, 3 w + (3×1 + 2) u = 53, 3(w + u)+ 2 u = 53, v = w + u, 3 v + 2 u = 53;
3 = 2×1 + 1, (2×1 + 1) v + 2 u = 53, v + 2(v + u)= 53, t = v + u, v + 2 t = 53.
Из полученных равенств последовательно находим
v = 53 - 2 t,
u = t - v = t - (53 - 2 t) = 3 t -53,
w = v - u = 53 - 2 t - (3 t -53) = 106 - 5 t,
z = u - w = 3 t -53- (106 - 5 t) = 8 t -159,
x = w - z = 106 - 5 t - (8 t -159) = 265 - 13 t,
y =2 x - z = 2(265 - 13 t) - (8 t -159) = 689 - 34 t.
Определение 2. Целая матрица D = (dij) размерности m ´ n называется матрицей канонического вида, если она обладает свойствами:
1) все элементы dij = 0 для любых i = 1, 2,…, m; j = 1, 2,…, n; i ¹ j;
2) все элементы dij ³ 0 для любых i = 1, 2,…, k, где k = min { m. n };
3) dii | di+ 1, i+ 1 для любых i = 1, 2,…, k- 1, где k = min { m, n }.
Теорема 5. Любую целую матрицу конечным числом элементарных преобразований строк и столбцов можно привести к матрице канонического вида, при этом r = rang A.
Диагональные элементы d 11,…, drr, r = rang A, матрицы канонического вида, эквивалентной матрице A, называются элементарными делителями матрицы A.
Теорема 4. Система ЛДУ разрешима тогда и только тогда, когда элементарные делители матрицы A и расширенной матрицы 
СЛДУ соответственно равны.
Пример 9. Выяснить разрешимость данной СЛДУ
Решение. Приводим матрицу и расширенную матрицу СЛДУ к каноническому виду.
,
Так как элементарные делители матриц равны, то данная СЛДУ разрешима.
Алгоритм решения СЛДУ Пусть дана СЛДУ. Запишем ее в матричном виде:
AX = B, (6)
Расширенную матрицу СЛДУ (6) расширим вторично, приписав к ней снизу единичную матрицу размерности n ´ n и нулевую матрицу размерности n ´1. Получим дважды расширенную матрицу СЛДУ:
.
Преобразуем матрицу A к каноническому виду D, выполняя элементарные преобразования над первыми m строками и первыми столбцами n матрицы 
. Тогда матрица B перейдет в матрицу F = U 1 B, где U 1 - произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E¢ перейдет в матрицу U 2, где U 2 - произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу:
.
Полученной матрице соответствует матричное уравнение:
DY = F, (7)
где Y = U 2-1 X, F = U 1 B, которому соответствует СЛДУ
(8)
Если хотя бы один из элементов fr + 1,…, fm не равен нулю, или хотя бы один из элементов fk не делится на число dkk (k =1, 2, …, r), то система (8), а поэтому и система (6) не имеют решений. Если же
d 11| f 1,…, drr | fr, fr + 1 = 0,…, fm = 0,
то разделим 1-е, 2-е, …, r -е уравнения системы (8) соответственно на числа d 11, d 22, …, drr находим y 1, y 2, …, yr. Значения неизвестных yr +1,…, yn можно брать произвольным образом: yr +1= t 1, …, yn = tn - r. Следовательно, находим:
.
Так как Y = U 2-1 X, то отсюда находим
X = U 2 Y, (9)
и оно зависит от n - r свободных переменных t 1, …, tn - r Î Z.
Пример 10. Решить диофантово уравнение:
4 x 1 + 17 x 2 + 31 x 3 - 21 x 4 = 17.
Решение. Составим дважды расширенную матрицу и приведем ее к каноническому виду:
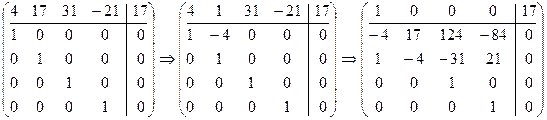
Отсюда находим
,
t 1, t 2, t 3 - свободные неизвестные. Тогда
.
Отсюда
, где t 1, t 2, t 3 Î Z.
Пример 11. Решить СЛДУ:
где a - произвольный целый параметр.
Решение. Составим дважды расширенную матрицу и приведем ее к каноническому виду:
.
Отсюда
где. Следовательно, x = a - 2 t, y = -3 a + 7 t, z = 4 a - 9 t, где t Î Z.