Теорема 1. Функция Эйлера j(m) обладает свойствами:
10 Функция Эйлера мультипликативна, т.е. если натуральные числа m и n взаимно просты, то j(mn) = j(m) j(n).
20 Если p –простое число, то j(p) = p - 1.
30 Если p –простое число,a Î N, то j(pa) = pa -1(p - 1) = pa (1 – 1/ p).
40 Если  – каноническое разложение числа m, то
– каноническое разложение числа m, то
 .
.
50  .
.
Пример.

Теорема 2 (теорема Эйлера). Для любого целого числа а взаимно простого с m выполняется сравнение
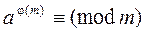 (1)
(1)
Теорема 3. Для любого простого числа p взаимно простого c числом a выполняется сравнение
 .
.
Сравнения с неизвестным. Сравнения первой степени с одним неизвестным
Определение 1. Пусть f (x) = a 0 xn + a 1 xn- 1+…+ an Î Z [ x ], a 0 T 0(mod m). Сравнением с неизвестной m-й степени по модулю m называется сравнение вида
f (x) º 0(mod m). (1)
Определение 2. Решением сравнения (1) по модулю m называется класс вычетов по модулю m, все числа которого удовлетворяют сравнению (1).
Так как имеется всего m классов по модулю m, то любое сравнение по модулю m можно решить не более чем за m испытаний, следующим способом.
Выписать некоторую полную систему вычетов по модулю m, например, 0, 1, 2, …, m -1, и проверить какие числа этой системы удовлетворяют сравнению. Соответствующие классы вычетов по модулю m дают решения сравнения.
Пример 1. Решить сравнение 2 x 5 + 3 x 3 - 4 x 2 + x - 2(mod 7).
Запишем полную систему вычетов по модулю 7: -3, -2, -1, 0, 1, 2, 3. Проверим, какие числа из ее удовлетворяют нашему сравнению (проверку можно вести по схеме Горнера, а вычисления проводить по модулю 7). В
| -4 | -2 | ||||||
| -3 -2 -1 | -1 | Да Да Да |
Сравнение имеет три решения `1,`3, `4 (mod 7).
Рассмотрим сравнение 1-й степени по модулю
axº b (mod m). (2)
Теорема 1. Пусть НОД(a, m) = d. Тогда справедливы утверждения:
1) если d F b, то сравнение (2) не имеет решений;
2) если (a, m) = 1, то сравнение (2) имеет единственное решении, которое находится по формуле:
 ; (3)
; (3)
3) если d | b, то сравнение (2) имеет d решений по модулю m, которые находятся по формулам:
 (4)
(4)
где x 0 - решение сравнения
 (5)
(5)
Умножим обе части сравнения на число 3, взаимно простое с модулем получим равносильное сравнение
15 x º 18(mod 7).
Так как 15 º 1(mod 7), 18 º 4(mod 7), то находим
x º 4(mod 7), `4 mod 7.
Для сравнительно небольших m сравнение можно решить по формуле (3) используя бинарный способ возведения в большую степень.
Пример 3. Решить сравнение 122 x º 142(mod 212).
Так как НОД(122, 212) = 2, и 2|142, то данное сравнение имеет 2 решения по модулю 142. Разделимо, обе части сравнения и модуль на число 2 и получим равносильное сравнение:
61 x º 71(mod 106).
Решаем последнее сравнение по формуле (3). Так как 106 = 2×53, то j(106)=1×52 = 52. Тогда по формуле (3) находим:

Отсюда по формулам (5) находим решения исходного сравнения  .
.
Третий способ наиболее быстрый и основан на алгоритме деления с остатком. Решаем сравнение (2) в случае (a, m) = 1. Для этого разложим рациональную несократимую дробь m/a в цепную дробь: m/a = [ a 1, a 2,…, ak,]. Тогда по свойству подходящих дробей будем иметь
mQk -1 – aPk -1 = (-1) k.
Отсюда находим
aPk -1(-1) k -1 º 1(mod m)
Тогда, умножая обе части сравнения (2) на
Умножим обе части сравнения (2) на Pk -1(-1) k -1 получим:
xº b Pk -1(-1) k -1(mod m). (7)
Пример 4. Решить сравнение 61 x º 71(mod 106).
Разлагаем число 106/61 в цепную дробь:
106 = 61×1 + 45,
61 = 45×1 + 16,
45 = 16×2+13
16=13×1+3
13 = 3×4+1
3=1×3
Итак, получаем 106/61 = [2, 15, 4]. Находим числители подходящих дробей
| i | |||||||
| ai | - | ||||||
| Pi |
Тогда по формуле (7) получаем xº 71×33(-1)6-1 º 95 (mod m).