Системы линейных сравнений по модулю. Китайская теорема об остатках

(2)

Если p простое число, то множество классов вычетов Z _p по модулю p является полем и для системы сравнений применимы все методы решений и основные теоремы, которые имеют место для теории СЛУ над полем.

Пример 1. Решить СЛС

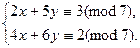
Способ 1. Метод Гаусса:

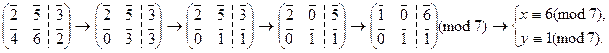
Все операции выполняются по модулю 7 или в роле Z ₇.

Способ 2. Правило Крамера:

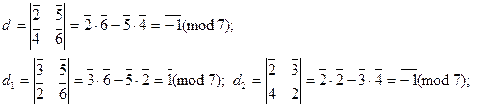
Тогда система равносильна системе

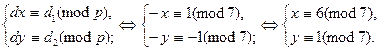
Ответ: .

Теорема 2. Система ЛC (2) разрешима тогда и только тогда, когда НОД (d_ii, m), элементарных делителей d_ii матрицы A делит соответствующие элементарные делители расширенной матрицы СЛС. 

Пример 2. Выяснить разрешимость данной СЛС

Решение. Приводим матрицу и расширенную матрицу СЛС к каноническому виду.

,

 

Так как элементарные делители матриц равны, то данная СЛС разрешима.

Алгоритм решения СЛС Пусть дана СЛС (2). Запишем ее в матричном виде:

AX º B (mod m), (3)

Расширенную матрицу СЛДУ (2) расширим вторично, приписав к ней снизу единичную матрицу размерности n ´ n и нулевую матрицу размерности n ´1. Получим дважды расширенную матрицу СЛДУ:

.

Преобразуем матрицу A к каноническому виду D, выполняя элементарные целочисленные приведенные преобразования над первыми m строками и первыми столбцами n матрицы . Тогда матрица B перейдет в матрицу F = U ₁ B, где U ₁ - произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E¢ перейдет в матрицу U ₂, где U ₂ - произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу:

.

Полученной матрице соответствует матричное уравнение:

DY º F (mod m), (4)

где Y = U ₂^-1 X, F = U ₁ B, которому соответствует СЛC

(5)

Если хотя бы один из элементов f_{r + 1},…, f_m не сравним с нулем по mod m, или хотя бы одно из чисел f_k не делится на D_k =НОД(d_kk, m), (k =1, 2, …, r), то система (5), а поэтому и система (2) не имеют решений. Если же

D ₁| f ₁,…, D _r | f_r, m | f_{r + 1},…, m | f_m,

то решаем 1-е, 2-е, …, r -е сравнения системы (5) по методу предыдущего параграфа y ₁, y ₂, …, y_r. Значения неизвестных y_{r +1},…, y_n можно брать произвольным образом: y_{r +1}º t ₁, …, y_n º t_{n - r} (mod m). Тогда система (2) имеет D ₁... D _r m^k-r решений по модулю m:

.

Так как Y = U ₂^-1 X, то отсюда находим

X ^{( j )} = U ₂ Y ^{( j )}, (12)

и оно зависит от n - r свободных переменных t ₁, …, t_{n - r} Î Z _m.

Пример 3. Решить СЛC:

Решение. Составим дважды расширенную матрицу и приведем ее к каноническому виду:

 

.

Отсюда приходим к системе сравнений вида (5):

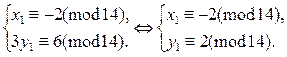
Отсюда

где t Î Z ₁₂. Таким образом, получаем решения сравнения:

.

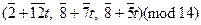Случай, когда дана СЛУ с различными модулями решается более сложно. Рассмотрим СЛС простейшего вида с одним неизвестным:

(6)

но с различными и попарно взаимно простыми модулями.

Теорема 3. Пусть числа m ₁,…, m_k – попарно взаимно простые, числа M ₁,…, M_k и M ₁´,…, M_k ´ определены из условий

m ₁… m_k = M_sm_s, M_s M_s´ º 1 (mod m_s), s = 1,2,…, k, (7)

и пусть

x ₀ = M ₁ M ₁ ´ b ₁ + M ₂ M ₂ ´ b ₂ +…+ M_k M_k´b_k (8)

Тогда совокупность всех значений x, удовлетворяющих системе (5), определяется сравнением

x º x ₀(mod m ₁… m_k). (9)

Пример 4. Решить систему сравнение:

Найдем числа M ₁, M₂ и M ₁´, M₂´ из условии (7):

M ₁ M ₁´ º (mod 5), M₂M₂´ º 1 (mod 6),

6 M ₁´ º 1(mod 5), 5 M ₂´ º 1 (mod 6),

M ₁´ º 1(mod 5), M ₂´ º 5 (mod 6),

Тогда число x ₀ вычислим о формуле:

x ₀ = M ₁ M ₁ ´ b ₁ + M ₂ M ₂ ´ b ₂ = 6×1×3 + 5×6×4 = 138 º 18 (mod 30).

Ответ: .

 

6. Сравнения n -й степени по простому и составному модулю

Пусть p – простое число. Пусть f (x) = a ₀ xⁿ + a ₁ x^{n- 1}+…+ a_n Î Z [ x ], a ₀ T 0(mod p). Рассмотрим сравнение

f (x) º 0(mod p). (1)

Так как кольцо классов вычетов Z _p по простому модулю p является полем, то рассматривая сравнение (1) как уравнение над конечным полем Z _p, можем применить к сравнению (1) всю теорию многочленов над конечным полем и получаем следующие теоремы.

Теорема 3. Если число решений сравнения (1) больше чем n решений, то все его коэффициенты делятся на p.

Следствие. Если a ₀ T 0(mod p), то число решений сравнения (1) не больше степени сравнения.

Теорема 5. Пусть m = m ₁… m_k, где числа m ₁,…, m_k попарно взаимно простые. Тогда сравнение

f (x) º (mod m) (5)

равносильно системе сравнений

(6)

при этом, число T решений сравнения (5) равно

T = T ₁… T_k,

где T ₁,…, T_k – обозначают соответственно число отдельных решений сравнений системы (6).

Теорема 6. Всякое решение x º x ₁ (mod p) сравнения (1) при условии, что f´ (x ₁) не делится на p, даст одно решение сравнения (9):

(10)

Пример 1. Решить сравнение

f (x) = 2 x ³ - x ² + 3 x +2 º 0 (mod 225). (13)

Так как 225 = 3²5², то это сравнение равносильно системе сравнений:

(14)

Решаем сравнения

методом испытаний, выполняя проверку по схеме Горнера:

a		-1
		-1			mod 3
					mod 3
					mod 3
		-1			mod 5
					mod 5
					mod 5
					mod 5
					mod 5

Первое сравнение имеет 1 решение x º 1(mod 3), второе сравнение имеет 1 решение x º 2(mod 5). Далее

f´ (x) = 6 x ² - 2 x + 3.

Так как

f´ (1) = 7 º 1 T 0(mod 3),

f´ (2) = 24 – 4 + 3 = 23 º 3 T 0(mod 5),

то каждое из сравнений (14) и сравнение (13) имеет по одному решению.

Решая первое из сравнений (14) положим x = 1 + 3 t ₁, где t ₁ – целое число. Подставляем это значение x в сравнение, получим

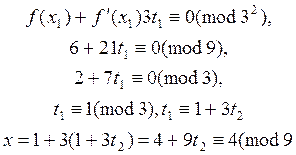
Решая второе из сравнений (14) положим x = 2 + 5 t ₁, где t ₁ – целое число. Подставляем это значение x в сравнение, получим

Все решения сравнения (13) являются решениями системы сравнений:

Найдем числа M ₁, M₂ и M ₁´, M₂´ из условии (7):

M ₁ M ₁´ º (mod 9), M₂M₂´ º 1 (mod 25),

25 M ₁´ º 1(mod 9), 9 M ₂´ º 1 (mod 25),

M ₁´ º 4(mod 5),

M ₂´ º 9¹⁹ º 9× (9 ²)⁹ º 9×6× (6 ²)⁴ º 4× (11 ²)² º 4× 4 ² º -4×9 º -11 (mod 25),

Тогда число x ₀ вычислим о формуле:

x ₀ = M ₁ M ₁ ´ b ₁ + M ₂ M ₂ ´ b ₂ = 25×4×4 - 9×11×12 = 112 (mod 225).

Ответ: 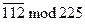.