ЛЕКЦИЯ
(16)
1. ПОТОКИ СОБЫТИЙ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
При рассмотрении процессов, протекающих в системе с дискретными состояниями и непрерывным временем, часто целесообразно представлять процесс так, как будто изменения состояний системы происходят под действием каких-то потоков событий.
Поэтому мы сейчас рассмотрим подробнее потоки событий и их свойства.
Поток событий - это последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.
Примеры потоков:
· поток вызовов на телефонной станции;
· поток включений приборов в бытовой электросети;
· поток покупателей;
· поток заказных писем, поступающих в почтовое отделение;
· поток грузовых составов, поступающих на железнодорожную станцию;
· поток неисправностей (сбоев) ПЭВМ;
· поток выстрелов, направляемых на цель, и т. д.
Поток событий можно изобразить последовательностью точек на оси времени 0—t, каждая из которых имеет определенную координату.
а) - поток событий,
б) - простейший поток.
Поток характеризуется интенсивностью (плотностью) потока λ – частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.
Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени.
Например, поток изделий на конвейере сборочного цеха (с постоянной скоростью движения) является регулярным.
Такой поток сравнительно редко встречается в реальных системах, но представляет интерес как предельный случай. Типичным для системы массового обслуживания является случайный поток заявок.
Рассмотрим потоки событий, обладающие некоторыми особенно простыми свойствами. Для этого введем ряд определений.
1. Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность стационарного потока есть величина постоянная:
λ (t) =λ. Другими словами, если вероятность попадания того или иного числа событий на элементарный участок времени длиной τ зависит только от длины участка и не зависит от того, где именно на оси t расположен этот участок.
Стационарность потока означает его однородность по времени; вероятностные характеристики такого потока не меняются в зависимости от времени. В частности, интенсивность (или «плотность») потока событий — среднее число событий в единицу времени — для стационарного потока должна оставаться постоянной. Это, разумеется, не значит, что фактическое число событий, появляющихся в единицу времени, постоянно, поток может иметь местные сгущения и разрежения. Важно, что для стационарного потока эти сгущения и разрежения не носят закономерного характера, а среднее число событий, попадающих на единичный участок времени, остается постоянным для всего рассматриваемого периода.
На практике часто встречаются потоки событий, которые (по крайней мере, на ограниченном участке времени) могут рассматриваться как стационарные. Например, поток вызовов, поступающих на телефонную станцию, скажем, на интервале от 12 до 13 часов может считаться стационарным. Тот же поток в течение целых суток уже не будет стационарным (ночью интенсивность потока вызовов гораздо меньше, чем днем).
Следует отметить, что так же обстоит дело и с большинством физических процессов, которые мы называем «стационарными» — в действительности они стационарны только на ограниченном участке времени, а распространение этого участка до бесконечности — лишь удобный прием, применяемый в целях упрощения.
2. Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени τ1 и τ2 число событий, попадающих на один из них, не зависит от числа событий попавших на другой. По сути, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга, вызванные каждое своими собственными причинами. Если такая зависимость появляется, условие отсутствия последействия оказывается нарушенным.
Например, поток пассажиров, входящих в метро, практически не имеет последействия. А вот поток покупателей, отходящих с покупками от прилавка, уже имеет последействие (хотя бы потому, что интервал времени между отдельными покупателями не может быть меньше, чем минимальное время обслуживания каждого из них).
3. Поток событий называется ординарным, если вероятность попадания на малый (элементарный) участок времени Δ t двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Другими словами, поток событий ординарен, если события появляются в нем поодиночке, а не группами (парами, тройками и т. д.).
Например, поток поездов, подходящих к станции, ординарен, а поток вагонов – неординарен.
Если в неординарном потоке события происходят только парами, только тройками и т. д., то можно его рассматривать как ординарный «поток пар», «поток троек» и т. д. Несколько сложнее обстоит дело, если число событий, образующих «пакет» (группу одновременно приходящих событий), случайно. Тогда приходится наряду с потоком пакетов рассматривать случайную величину X — число событий в пакете, и математическая модель потока становится более сложной.
2.1. ПРОСТЕЙШИЙ ПОТОК
Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия.
Название «простейший» объясняется тем, что СМО с простейшими потоками имеет наиболее простое математическое описание. Между прочим, самый простой, на первый взгляд, регулярный поток не является «простейшим», так как обладает последействием: моменты появления событий в таком потоке связаны жесткой, функциональной зависимостью. Без специальных усилий по поддержанию его регулярности такой поток обычно не создается.
Именно из-за этого последействия анализ процессов, связанных с регулярными потоками, оказывается, как правило, труднее, а не легче по сравнению с простейшими.
Простейший поток в качестве предельного возникает в теории случайных процессов столь же естественно, как в теории вероятностей нормальное распределение получается в качестве предельного для суммы случайных величин. При наложении (суперпозиции) достаточного большого числа n независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивностям λ i (i =1,2,..., n) ) получается поток, близкий к простейшему с интенсивностью λ, равной сумме интенсивностей входящих потоков, т.е.
λ = Σ λ i
Дополнительно требуется, чтобы складываемые потоки были сравнимы по интенсивности, т. е., чтобы среди них не было, скажем, одного, превосходящего по интенсивности сумму всех остальных.
Если поток событий не имеет последействия, ординарен, но не стационарен, он называется нестационарным пуассоновским потоком. В таком потоке интенсивность λ (среднее число событий в единицу времени) зависит от времени:
λ = λ(t),
тогда как для простейшего потока
λ = const.
Название «пуассоновский» поток связано с тем, что при соблюдении определений 1 – 3 число событий, потока попадающих на любой фиксированный интервал времени (любой участок), будет распределено по закону Пуассона.
Поясним, что это означает.
Рассмотрим на оси t, где наблюдается поток событий, некоторый участок времени длины τ, начинающийся в момент t0 и заканчивающийся в момент t0+ τ (см. рис. а).
Нетрудно доказать (доказательство дается во всех курсах теории вероятностей), что вероятность попадания на этот участок ровно τ событий и выражается формулой:
(1)
где а — среднее число событий, приходящееся на участок t;
е — основание натуральных логарифмов.
Для стационарного (простейшего) пуассоновского потока величина а равна интенсивности потока, умноженной на длину интервала:
а= λτ,
т. е. не зависит от того, где на оси t находится период τ. Для нестационарного пуассоновского потока величина а зависит от того, в какой точке t0 начинается участок t.
Рассмотрим на оси t простейший поток событий с интенсивностью λ (рис. б). Нас будет интересовать случайный интервал времени Т между соседними событиями в этом потоке.
Найдем его закон распределения.
Сначала найдем функцию распределения:
P(t)= P(T<t),
т. е. вероятность того, что величина Т будет иметь значение, меньшее, чем t.
Отложим от начала интервала Т (точки t0) отрезок t и найдем вероятность того, что интервал Т будет меньше t. Для этого нужно, чтобы на участок длины t, примыкающий к точке t0 попало хотя бы одно событие потока.
Вычислим вероятность этого P(t) через вероятность противоположного события (на участок t не попадет ни одного события потока):
P(t)=1- P0.
Вероятность P0 найдем по формуле (1), полагая m = 0:
откуда функция распределения величины Т будет:
(2)
Чтобы найти плотность распределения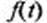 
случайной величины Т, необходимо продифференцировать выражение (2) по t:
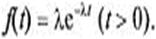(3)
Закон распределения с плотностью (3) называется показательным (или экспоненциальным). Величина λ называется параметром показательного закона.
Показательный закон распределения играет большую роль в теории марковских случайных процессов.
Найдем числовые характеристики.
Для случайной величины Т — математическое ожидание (среднее значение) M(t) = mt и дисперсия Dt имеют вид
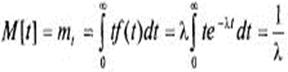(4)
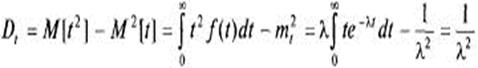. (5)
Извлекая корень квадратный из дисперсии, найдем среднее квадратическое отклонение случайной величины Т.
(6)
Итак, для показательного распределения математическое ожидание и среднее квадратическое отклонение равны друг другу и обратно пропорциональны λ — интенсивности потока.
Приведем выражение для так называемого «элемента вероятности появления события» или вероятности наступления на элементарном участке τ (рис а) события потока.
Найдем вероятность того, что на участке τ = Δ t появится какое-то событие потока, т. е. участок не будет «пуст». Так как поток ординарен, вероятностью появления на участке более чем одного события можно пренебречь. Обозначим P0(Δ t) вероятность того, что на участке 
не будет события, а P1(Δ t) — вероятность того, что на нем появится одно событие.
В силу ординарности потока
P1(Δ t) = 1 - P0(Δ t),
а вероятность P0(Δ t) определяется по (1):
Откуда
Разлагая 
в ряд и пренебрегая величинами высшего порядка малости, получаем:
(7)
Эта вероятность и называется «элементом вероятности появления события».
Очевидно, такая же формула будет справедлива и для нестационарного пуассоновского потока с той разницей, что величину λ (t) нужно брать равной ее значению в той точке t, к которой примыкает участок Δ t.
1.2.ПОТОК ПАЛЬМА.
Поток событий называется потоком Пальма (или потоком с ограниченным последействием), если промежутки времени между последовательными событиями:
T1, T2, T3, …, Ti, …,