Отчет по лабораторной работе №2
«Абсолютно упругое и неупругое механическое взаимодействие»
Студента группы К-13 Станкевич А.М
Вариант 1
Цель работы:
1)Изучение физических моделей механического взаимодействия в форме абсолютно упругого и неупругого соударения двух тел-шаров разной массы; движущихся с разными скоростями;
2)исследование физических характеристик,сохраняющихся при таких взаимодействиях экспериментальное определение энергетических потерь при неупругом взаимодействии
Соударение тележек
Схема опыта для заданий 1,2.
 Рис. 1
Рис. 1
Рабочая схема модели представляет собой два тела(тележки),которые могут двигаться без трения в ограниченной области сталкиваются друг с другом по схеме абсолютно упругого и неупругого ударов.(столкновение со стенками-всегда абсолютно упругое). Массы тел и скорости задаются в режиме «стоп» и меняются в ходе выполнения заданий.
Анализируется только кинетическая энергия поступательного движения тел.
Кинетическая энергия (Т), скорости и импульса тел рассматриваются компьютером
Соударение шаров.
Схема опыта для задания 3
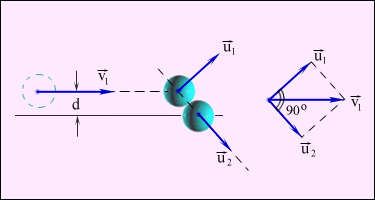
Обработка результатов измерений.
Задание 1
Результаты измерений для абсолютного упругого центрального удара.
| № измерений | V₂ м/с | V₁ м/с | р₁ кгˑм/с | р₂ кгˑм/с | р΄₁ кгˑм/с | P΄₂ кгˑм/с | T₁+T₂=E | T΄₁+T΄₂=E΄ | |
| -2 | -2 | -2 | -2 | 0,50+2,00=2,50 | 0,50+0,00=0,50 | ||||
| -1 | -1 | -1 | -1 | 0,50+0,50=1,00 | 0,50+0,50=1,00 | ||||
| 0,50+0,00=0,50 | 0,50+0,50=1,00 |
Результаты расчётов для абсолютного упругого центрального удара.
| № измерений | V₂ м/с | (р₁+р₂) кгˑм/с | (р΄₁+р΄₂) кгˑм/с | T₁+T₂=E | T΄₁+T΄₂=E΄ | ΔU=E-E΄ |
| -2 | -1 | -1 | 0,50+2,00=2,50 | 0,50+0,00=0,50 | ||
| -1 | 0,50+0,50=1,00 | 0,50+0,50=1,00 | ||||
| -1 | 0,50+0,00=0,50 | 0,50+0,50=1,00 |
Расчеты
р₁+р₂=[кгˑм/с ] р₁΄+р΄₂=[кгˑм/с ]
1. р₁+р₂= -1[кгˑм/с ] 1.р₁΄+р΄₂=-1[кгˑм/с ]
2. р₁+р₂=0[кгˑм/с ] 2.р₁΄+р΄₂=0[кгˑм/с ]
3. р₁+р₂=1[кгˑм/с ] 3.р₁΄+р΄₂=1[кгˑм/с ]
ΔU=E-E΄
1. ΔU=2,50-2,50=0
2. ΔU=1,00-1,00=0
3. ΔU=0,50-0,50=0
Задание 2
Исследование центрального неупругого удара
Результаты измерений для абсолютного упругого центрального удара.
| № измерений | m₂ кг | V₂ м/с | T₁+T₂=E Дж | T΄₁+T΄₂=E΄ Дж | р₁ кгˑм/с | р₂ кгˑм/с | р΄₁ кгˑм/с | P΄₂ кгˑм/с |
| -2 | 0,50+2,00=2,50 | 0,12+0,12=0,24 | 1,00 | -2,00 | -0,50 | -0,50 | ||
| -1 | 0,50+0,50=1,00 | 0,00+0,00=0,00 | 1,00 | -1,00 | 0,00 | 0,00 | ||
| 0,50+0,00=0,50 | 0,12+0,12=0,24 | 1,00 | 0,00 | 0,50 | 0,50 | |||
| -2 | 0,50+4,00=4,50 | 0,50+1,00=1,50 | 1,00 | -4,00 | -1,00 | -2,00 | ||
| -1 | 0,50+1,00=1,50 | 0,06+0,11=0,17 | 1,00 | -2,00 | -0,33 | -0,67 | ||
| 0,50+0,00=0,50 | 0,06+0,11=0,17 | 1,00 | 0,00 | 0,33 | 0,67 | |||
| -2 | 0,50+6,00=6,50 | 0,78+2,34=3,12 | 1,00 | -6,00 | -1,25 | -3,75 | ||
| -1 | 0,50+1,50=2,00 | 0,12+0,38=0,50 | 1,00 | -3,00 | -0,50 | -1,50 | ||
| 0,50+0,00=0,50 | 0,03+0,09=0,12 | 1,00 | 0,00 | 0,25 | 0,75 |
Результаты рассчетов для абсолютного упругого центрального удара.
| № измерений | (р₁+р₂) кгˑм/с | (р΄₁+р΄₂) кгˑм/с | 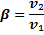
| 𝛇= 
| 
| 
|
| -1,00 | -1,00 | -2 | 0,90 | 0,90 | ||
| 0,00 | 0,00 | -1 | 1,00 | 1,00 | ||
| 1,00 | 1,00 | 0,50 | 0,50 | |||
| -3,00 | -3,00 | -2 | 0,50 | 0,67 | 0,67 | |
| -1,00 | -1,00 | -1 | 0,50 | 0,89 | 0,89 | |
| 1,00 | 1,00 | 0,50 | 0,66 | 0,66 | ||
| -5,00 | -5,00 | -2 | 
| 0,52 | 0,52 | |
| -2,00 | -2,00 | -1 | 
| 0,75 | 0,75 | |
| 1,00 | -1,00 | 
| 0,76 | 0,76 |
Задание 3
Исследование косого центрального упругого удара
Результаты измерений и расчётов для прямого центрального упругого удара.
| № измерений | 
| V₁ м/с | V₂ м/с | α₁ | α₂ | V₁cosα₁ м/с | V₂sinα₁ м/с | V₂cosα₂ м/с | V₂sinα₂ м/с | V₁² м²/с² | V₂² м²/с² | |
| 0.0 | 2.7 | 1.3 | -2.5 | 1.3 | 7.3 | 1.7 | ||||||
| 0.2 | 2.7 | 1.3 | -1.5 | 3.5 | 1.1 | -0.7 | 7.3 | 1.7 | ||||
| 0.4 | 2.9 | 1.2 | 1.5 | 5.4 | 0.5 | -1.1 | 8.4 | 1.4 | ||||
| 0.5 | 1.2 | 1.2 | 3.1 | 5.9 | 0.2 | -1.2 | 9.6 | 1.4 | ||||
| 0.8 | 3.6 | 0.8 | 7.7 | -1.6 | -0.7 | 0.3 | 0.6 | |||||
Вычесления
Задание 2:
β=  ζ=
ζ= 
β₁‚₄‚₇=  =-2ζ₁‚₂‚₃=
=-2ζ₁‚₂‚₃= 
β₂‚₅‚₈=-1 ζ₂‚₅‚₆= 
β₃‚₆‚₉=  ζ ₇‚₈‚₉=
ζ ₇‚₈‚₉= 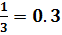
 =
= 
δизм₁= 
δизм₂= 
δизм₃= 
δизм₄=  =0,67
=0,67
δизм₅=  =0,89
=0,89
δизм₆= 
δизм₇= 
δизм₈=  =0,75
=0,75
δизм₉=  =0,76
=0,76
δрасп= 
δрасп₁=0,90
δрасп₂=1,00
δрасп₃=0,50
δрасп₄=0,67
δрасп₅=0,89
δрасп₆=0,67
δрасп₇=0,52
δрасп₈=0,75
δрасп₉=0,76
Задание 3
V₁·cosα₁=Vₒ-  V₂cosα
V₂cosα
1. 4-5ˑ1.3ˑcos0=4-5ˑ1.3=-2,5[ м/с]
2. 4-5ˑ1,3ˑcos12=-1,5[ м/с]
3. 4-5ˑ1.2cos24=1,5[ м/с]
4. 4-5ˑ1.2cos30=3,1[ м/с]
5. 4-5ˑ0,8cos53=7,7[ м/с]
V₁·sinα₁=-  V₂sinα₂
V₂sinα₂
1. -5ˑ1,3ˑsin0=0 [ м/с]
2. -5ˑ1,3sin12=3,5[ м/с]
3. -5ˑ1,2sin24=5,4[ м/с]
4. -5ˑ1,2sin30=5,9[ м/с]
5. -5ˑ0,8sin53=-1,6[ м/с]
V₂·cosα₂=(Vₒ-V₁cosα₁) 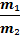
1. (4+2,5)ˑ1/5=1,3[ м/с]
2. (4+1,5)ˑ1/5=1,1[ м/с]
3. (4-1,5)ˑ1/5=0,5[ м/с]
4. (4-3,1)ˑ1/5=0,2 [ м/с]
5. (4-7.7)ˑ1/5=-0,7[ м/с]
V₂·sinα₂=-V₁sinα₁ 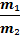
1. 0ˑ7/5=0[ м/с]
2. -3,5ˑ1/5=-0,7 [ м/с]
3. -5,4ˑ1/5=-1,1[ м/с]
4. -5,9ˑ1/5=-1,2 [ м/с]
5. 1,6ˑ1/5=0,3 [ м/с]
Выводы
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).