Надежностьобъектовнарушаетсявозникающимиотказами.Отказырассматриваюткакслучайныесобытия.Дляколичественнойоценкинадежностииспользуютсяметодытеориивероятностииматематическойстатистики.Показателинадежностимогутопределятьсячистоаналитическим путем на основе математической модели - математическоеопределениенадежности.Показателинадежностимогутопределятьсяврезультатеобработкиопытныхданных-статистическоеопределениепоказателянадежности.
Момент возникновения отказа, частота возникновения отказов -величиныслучайные.Поэтомубазовымиметодамидлятеориинадежностиявляются методы теории вероятности и математической статистики. Случайное событие - событие, которое при осуществлениисовокупностиусловийS можетлибопроизойти,либонепроизойти.
СлучайноесобытиехарактеризуетсявероятностьюреализацииР.
Случайная величина - величина, которая в результате опыта принимаетодно,напереднеизвестноезначение,зависящееотслучайныхпричин.Случайныевеличинымогутбытьдискретнымиинепрерывными.
Все, возможные на практике, значения некоторой случайной величиныобразуютгенеральнуюсовокупностьслучайной величины:
X (x 1 ,x 2,... xn)-генеральнаясовокупностьслучайнойвеличиных.
Рядконкретныхреализацийслучайнойвеличиныназываютвыборочной совокупностьюиливыборкой.
Генеральнаясовокупностьхарактеризуетсястатистическимипараметрами: математическоеожидание -среднеезначениеслучайнойвеличины;д исперсия -мерарассеиванияслучайнойвеличиныотносительн ос реднегозначения:
σ =√ D
где - среднее квадратическое (стандартное) отклонение случайной
величины.
Напрактикематематическоеожиданиеидисперсиюслучайнойвеличиныможнотолькооценитьнаосновевыборкиизконечногочисланаблюдений(измерений)случайнойвеличины:
-выборочноесреднееарифметическоезначениеслучайнойвеличины
1 n
x =∑ xi
| n |
где n-числонаблюдений,xi-реализацияслучайнойвеличинывкаждомнаблюдении.
- исправленное выборочное среднее квадратическое значениеслучайнойв еличины (выбор очноестандартное отклонение)
s =√ 1
n
∑(x − x)2
n −1 i =1 i,
гдеs-выборочноесреднееквадратическое(стандартное)отклонениеслучайнойвеличины,являющеесяоценкойстандартногоотклонениягенеральнойсовокупности.
Кромесреднегоарифметическогодляоценкиматематическогоожидания могут использоваться медиана и мода, а для оценки дисперсии -размах.
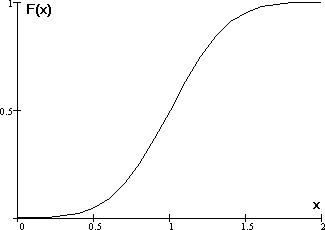
Рис.5.
Случайная величина
характеризуется закономраспределения,которыйсвязываетзначенияслучайнойвеличинысвероятностьюихпоявления.Дляхарактеристики закона распределенияслучайнойвеличиныиспользуютсяследующиефункции.
Функция распределенияслучайной величины - функция F(х),определяющая вероятность того, чтослучайнаявеличинаХврезультате
испытанийприметзначение,меньшеилиравноех
F (x)= P (Χ ≤ x).
Функция распределения случайной величины может быть представленаграфиком(рис. 5).
Плотностьраспределения вероятностейслучайнойвеличины
f (x)= F' (x), f (x)≥0,
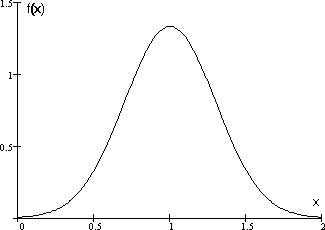плотность вероятностихарактеризуетвероятностьтого,чтослучайная величина приметконкретноезначениеx(рис.6).
Плотностьвероятностиифункцияраспределения связанызависимостью
x
F (x)=∫ f (x) dx
−∞.
Рис.6.
Показателинадежностимогутрассчитыватьсянаосновефункции
распределения и плотности распределения (математическое определение), атакженаосновестатистическихданныхэксплуатацииииспытаний(статистическое определение)
Экспериментальной оценкой плотности вероятности случайной
величиныявляетсягистограммараспределения случайнойвеличины(рис. 7).
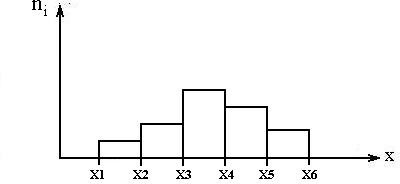Гистограммапоказываетзависимость количестванаблюдаемых значений случайнойвеличинывопределенноминтервалезначенийотграницэтихинтервалов.Погистограммеможноприближенносудитьоплотности распределенияслучайнойвеличины.
Рис.7.
При построениигистограммыв выборке случайной
величины x из n значений определяют наибольшее xmax и наименьшее xminзначения.Диапазон изменениявеличины
Δx = x min− x max
разбиваютнаmодинаковыхинтервалов.Затемподсчитываютчислонаблюдаемых значений случайной величины ni, попадающих в каждый i-тыйинтервал.
Прианализеирасчетепоказателейнадежностиматематическимметодом необходимо знать функцию распределения и функцию плотностираспределениявероятностиоцениваемогопараметра.Напрактикеиспользуютсятиповыезаконыраспределенияслучайнойвеличины,ккоторым весьма близки реальные распределения показателей надежности вовремени.
Нормальноераспределение. Является основным вматематической статистике. Оно образуется, когда на случайную величинудействует большое количество факторов. В теории надежности нормальнымраспределениемописываютнаработкинаотказобъектоввследствиеихизносаистарения.
Нормальныйзаконраспределенияхарактеризуетсядвумястатистическими параметрами: математическим ожиданием µ и стандартнымотклонением σ. Для оценки математического ожидания можно использоватьсреднееарифметическоезначениеслучайнойвеличины.Статистическиепараметры нормальногораспределения
1 n
μ ≈ t = M (t)=∑ ti
| n, |
где t -среднееарифметическоезначениепараметра(временнойпараметр),ti–выборочные значенияслучайной величины
| n −1 |
| n |
= D (t)= ∑(ti − t)
i =1,
σ–стандартноеотклонениеслучайнойвеличины,D(t)-дисперсияслучайнойвеличины.
Характернормальногораспределенияопределяетсяфункциямираспределенияивероятностиплотностислучайнойвеличины.Функцияраспределения случайной величины при нормальном законе распределения(рассматриваемвременнойпараметр,посколькупоказателинадежностиявляютсявременнымихарактеристиками)
| t |
−
F (t)=∫ f (t) dt = 1 ∫ e
2 σ 2 dt
−∞ σ √2 π −∞,
плотностьвероятностинормальногозаконараспределения
(t − t)2
| e |
σ √2 π
2 σ 2
.
СпомощьюнормальногораспределенияможноописатьвероятностьотказаобъектавследствиеегостаренияилиизносаQ(t)=F(t)взависимостиот
наработки объекта t.Вероятностьбезотказнойработывэтомслучае
P (t)=1− F (t).
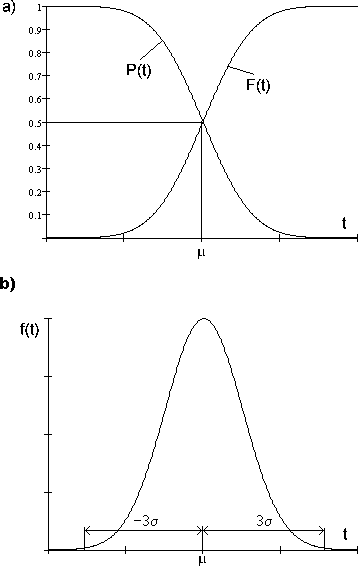
Зависимость P(t)называют такжекривой(функцией)убылиресурсов.
Нарис.14a)показаныграфикифункциинормальногораспределения исоответствующейейкривой убылиресурсов.
Математическомуожиданию μсоответствуетуровеньвероятности 0,5.
Общий видграфикаплотностивероятности при
Рис.14.
нормальном распределении показан нарис. 14 b). В границах± 3относительно среднего значения укладывается 99,73 % значений случайнойвеличины. Эти границы часто используются для оценки пределов изменениязначенийслучайнойвеличиныпринормальномеераспределении.
Длявыполнениярасчетовсиспользованиемнормальногораспределенияприменяютнормированноенормальноераспределение(табулированнуюфункциюЛапласадлявероятностипопаданиянормированнойнормальнойвеличиныХвинтервал(0,x):
Φ (x)=0,5+
| x |
1 ∫ e
− x 2
2 dx
¿
x = t − t
√2 π 0,
где
σ -квантильнормированногонормальногораспределения.
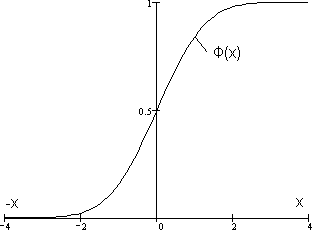Нарис.15показанграфикнормированногонормальногораспределения.ВтаблицахприводятсязначенияФ(х)дляположительныхквантилих.Дляотрицательных значений квантиливероятность равна
Φ (− x)=1− Φ (x).
Нормированноенормальноераспределение удобноиспользоватьприрасчетахкаквероятностислучайнойвеличины,
Рис.15.
случайнойвеличиныпоеевероятности. так и для расчета значения
Для вычисления вероятности P (t 1≤ t ≤ t 2)попадания случайной
| ¿ |
| ¿ |
Еслинеобходиморешитьобратнуюзадачу:определитьнаработку,соответствующую заданной вероятности безотказной работы, то используютквантилинормального распределения
t = t + x ⋅ σ,
где x - квантиль нормированного нормального распределения, котораязависитоттребуемойвероятностииприводитсявтаблицах.
Нормальному распределению подчиняется наработка на отказ многихвосстанавливаемыхиневосстанавливаемыхобъектов.
Пример1.Наработкаобъектадоотказаимеетнормальноераспределение с математическим ожиданием μ = 1000 час и стандартнымотклонениемσ=200час.Определитьвероятностьбезотказнойработыобъектавтечение400час.
Решение:
Вероятностьбезотказнойработыможетбытьвычисленачерезфункциюраспределения
| ∫ |
P (400)=1− F (400)=1− ⋅ e
(x −1000)2
2⋅2002 dx
200⋅√2 π −∞.
ДлярасчетаиспользуемтабулированноенормированноенормальноераспределениеФ(х).Определимквантильраспределения
x = x − μ = 400−1000 =−3
σ 200,
Для отрицательного значения квантили Φ (− x)=1− Φ (x).
Вероятностьбезотказнойработыравна
P (T)=1− Φ (− x)= Φ (x).
Вычисляемзначениевероятности,используятабулированнуюфункциюФ(х)
P (400)= Φ (3)=0,99865.
Вероятность безотказной работы объекта в течение 400 час составляет99,865%.
Пример 2.Определить вероятность безотказной работы подшипникакачениявтечение1500час,еслиегоресурспоизносуподчиняетсянормальному закону распределения с математическим ожиданием 3500 час истандартнымотклонением 1000час.
Решение:
Вычисляемквантильнормированногонормальногораспределения
x = x − μ = 1500−3500 =−2
σ 1000.
Вероятностьбезотказнойработы
P (1500)=1− Φ (−2)= Φ (2)=0,9772.
Вероятностьбезотказнойработыподшипникавтечение1500чассоставляет97,72%.
Пример3.Наработкаобъектадоотказаподчиняетсянормальномузакону распределения с параметрами µ = 1000 час и σ = 200 час. Определитьгамма-процентныйресурсобъекта привероятности90%.
Решение:
Определим вероятность отказа Φ (x)=1− P (x)=1−0,9=0,1. По
таблиценормированногонормальногораспределениянаходимквантиль,
соответствующуювероятности0,1: х=-1,281.Используемвыражениедлязначенияслучайнойвеличины
Tрγ = μ + x ⋅ σ =1000−1,281⋅200=744,
следовательно,90%ресурсизделияравен Tр 90=744 час.
Экспоненциальное распределение. Этот закон описывает надежностьработы изделия в период его нормальной эксплуатации, когда постепенныеотказывследствиеизносаистаренияещенепроявляютсяинадежностьхарактеризуетсявнезапнымиотказами.Этиотказывызываютсянеблагоприятнымсочетаниемразличныхфакторовиимеютпостояннуюинтенсивность.Экспоненциальноераспределениечастоназываютосновным законом надежности. Экспоненциальное распределение наиболееприменимо для оценки безотказности объектов в период после приработки идопроявленияпостепенныхотказов.Этотзакониспользуетсятакжеприрешениизадачоб обслуживаниисложныхсистем.
Экспоненциальноераспределениеимееттолькоодинпараметрλиявляется частным случаем распределения Вейбулла и гамма - распределения.Функция распределения случайной величины при экспоненциальном законераспределения
F (t)=1− e − λt
,
плотностьвероятностиэкспоненциальногораспределения
f (t)= dF (t) = λe − λt
dt,
Функцияраспределенияописываетвероятностьвозникновенияотказовобъекта.Вероятностьбезотказнойработыможетбытьопределенакак
t
P (t)=1− F (t)=
∫ λ (t) dt
| − λt |
| , |
где-интенсивностьотказов.При λ ≤0,1можнопринять
P (t)≈1− λt.
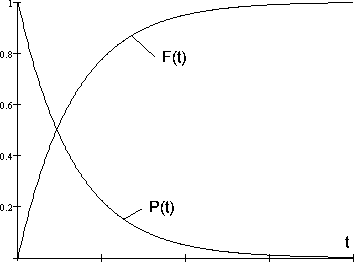
Экспоненциальноераспределениеиллюстрируетсяграфиками функциираспределения F(t) ивероятности безотказнойработыP(t),показаннымина рис. 16. Этораспределениесправедливо дляположительных значений
Рис.16.
случайнойвеличины.
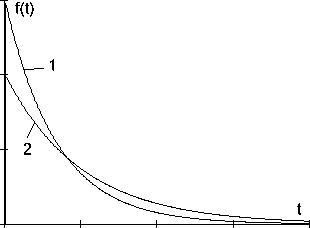
Графикиплотностивероятностислучайнойвеличиныприэкспоненциальном распределении приведены на рис. 17. График 1 построендля параметра λ = 0,0015, а график 2 – для λ = 0,001. Начальное значение награфике равноλ.
Математическое ожидание и среднее квадратическое отклонение дляэкспоненциальногозакона равнымежду собой
μ ≈ t = 1
λ,
σ = 1
λ.
Равенство μ = σ являетсясущественным признаком дляотнесения экспериментальногораспределенияктеоретическомуэкспоненциальномураспределению.
Рассмотрим примерыиспользования законаэкспоненциальногораспределения для расчетовнадежности.
Пример 1. Наработка на
Рис.17.
отказ сложной технической
системыподчиняетсяэкспоненциальномузаконураспределенияспараметром λ = 15*10-5 час-1. Определить вероятность безотказной работысистемывтечение100часинайтисреднеезначениенаработкинаотказ.
Решение:
ОпределимвероятностьбезотказнойработыпринаработкеTчерезфункциюраспределенияэкспоненциального закона
P (T)=1− F (x)=1− e − λ ⋅ x,
послеподстановкиконкретныхзначенийполучим
P (100)=1− e −15⋅10−5⋅100=0,985
.
Следовательно,вероятностьнаработки100чассоставляет98,5%.Среднеезначениенаработкиможетбытьопределеночерезпараметрраспределенияλ
T = μ = 1 = 1 =6677
o λ 15⋅10−5час.
Пример2.Интенсивностьотказовэлектрическогоэлементаравнаλ=10-
61/час.Отказыподчиняютсяэкспоненциальномузаконураспределенияслучайнойвеличины.Найтивероятностьбезотказнойработыэлементавтечение10000 час.
Решение:
Используем формулу для вероятности безотказной работы приэкспоненциальномраспределении
| , |
следовательно,вероятностьбезотказнойработыэлемента P(10000)=99%.
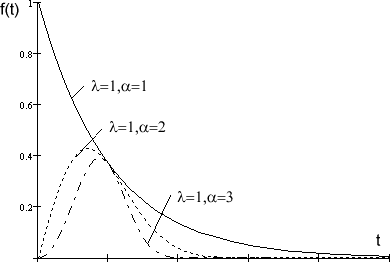
Распределение Вейбулла. Вейбулл описал с его помощью разбросусталостной прочности стали, предела ее упругости, размер частиц копоти идр. Это распределение применяют также при описании надежности сложныхтехническихсистем.
РаспределениеВейбуллаявляетсядвухпараметрическимуниверсальным законом, так как при изменении параметров оно в пределеможет описывать нормальное распределение, логарифмически нормальноераспределение,экспоненциальноеидр.РаспределениеВейбуллахарактеризуетсяпараметроммасштабаλипараметромформыα.
ФункцияраспределениядлязаконаВейбуллаимеетвид
| , |
функциянадежности
| , |
где-параметрформыкривойраспределения,-параметрмасштаба.
ПлотностьвероятностираспределенияВейбуллавыражаетсязависимостью
f (t)= dF ( t ) = αλtα −1 e − λtα
dt.
ЕслидлязаконаВейбуллапринятα=1,тополучимэкспоненциальноераспределение,котороеявляетсячастнымслучаемраспределенияВейбулла.
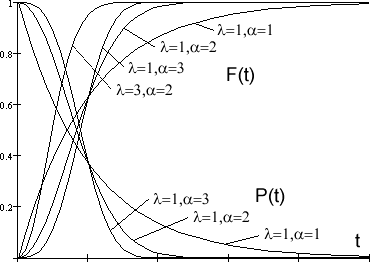ГрафикифункцийраспределенияF(t)ивероятностибезотказной работыP(t)показанынарис.
18.Приувеличениипараметраформыαкривая приближаетсяк нормальномураспределению.
Графикиплотностивероятности
Рис.18.
распределения
Вейбулла приведены на рис. 19. Влияние параметра формы на вид кривой вэтом случае выражены еще резче. При увеличении параметра форма кривойот экспоненциальной зависимости стремится к характерной для нормальногораспределенияколоколообразнойкривой.
Выборомпараметровмасштабаλиформыαможновширокихпределахизменятьформукривой,чтопозволяетиспользоватьзаконВейбулладля самых разных случаев математического описания надежности многихобъектов.
СтатистическиепараметрыраспределенияВейбуллавычисляютсячерезпараметрыαиλ.МатематическоеожиданиедлязаконаВейбулла
Γ (1+ 1)
| 1 |
λα,
стандартноеотклонение
| Рис.19. |
| Γ (1+2)− Γ 2(1+1) |
λα,
| √ |
| σ = |
| α |
| α |
∞
Γ (1+ α)=∫ t 2 e − tdt
0.
Длявычислениязначениягамма-функцииГ(n+),гдеn-целоечисло,
-дробноечислопри2≤n≤6можноиспользоватьболеепростуюформулу
Γ (n + α)=(n −1+ α)(n −2+ α)...(1+ α) Γ (1+ α).
При n 6 значения Г(n+) можно находить по формулеГ(n+1)=n!
Рассмотримпример использования распределения Вейбулла для
расчетанадежности.
Пример 1. Определить вероятность безотказной работы генератора втечение 1000 час, если его наработка на отказ описывается распределениемВейбулла спараметрамиα=2 иλ=6,667*10-7.
Решение:
Вероятностьбезотказнойработыравна
| . |
Следовательно,вероятностьбезотказнойработыгенераторавтечение1000час составляет51,3 %.
Пример2.СлучайнаянаработкаизделиядоотказараспределенапозаконуВейбулласпараметрами α =2, λ =10−6.Найтивероятностьбезотказнойработыизделияпризаданнойнаработке Tγ =300час.
Решение:
ИспользуемформулудлярасчетавероятностибезотказнойработыприраспределенииВейбулла
P (300)=
− λ ⋅ Tγα −10−6⋅3002 −10−6⋅9⋅104
| e = e = e =0,9139 |
Следовательно,вероятностьбезотказнойработывтечение300чассоставляет91,39 %.
Пример3.Дляпредыдущегопримеранайтинаработкудоотказапривероятности безотказной работы99%.
Решение:
Используемуравнениевероятностибезотказнойработы
0,99= e 99
откуда
ln0,99=−10−6⋅ T
992,
| √ |
T 99
= ln0,99 =100
−10−6
час.
Гамма–распределение. Распределениехарактеризуетсядвумяпараметрами:λ–параметрмасштабаиα–параметрформы.Оноимеетограничение с одной стороны(0 t ). Если параметр формы кривой -целоечисло,тогамма-распределениесписываетвремя,необходимыедляпоявления событий (например, отказов) при условии, что они независимы ипоявляются с постоянной интенсивностью . Это распределение описываетнаработкусистемысрезервированием,времявосстановления,атакжераспределение постепенных отказоввследствие износа.
Кривые распределения изменяют свою форму в широких пределах приизменениипараметров λиα.Функция гамма-распределения
F (t)=
λα
Γ (α)
t
∫ tα −1 e − λtdt
,F(t) ≡0 приt‹0.
Плотностьвероятностигамма-распределения(0,0)
f (t)=
λα
Γ (α)
∞
tα −1 e − λt
при t ≥ 0, f (t)≡0 при t < 0,
где
Γ (α)=∫ tα −1 e − t dt
-гамма-функция.
Вероятностьбезотказнойработы
| = |
Рис.20.
параметровраспределения.
λα
Γ (α)
t
∫ tα −1 e − λtdt
0.
Графики
для функцийраспределенияF(t) и
вероятностибезотказнойработы P(t)приведены нарис. 20.
Характерзависимостейизменяется вширокихпределах приизменении
Графики для плотности вероятности гамма-распределения показаны нарис. 21.При 1 характерзависимостидляплотностираспределенияубывающий.При=1и λ = Const получаетсяэкспоненциальноераспределение,при3криваяраспределенияприближаетсякнормальному
законураспределения.
Математическоеожиданиеидисперсиядлягамма-распределениясоответственноравны
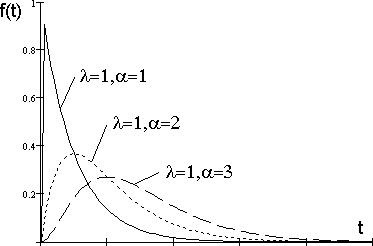
Рис.21.
μ = M (t)= α
λ и
σ 2= D (t)= α
λ 2.
Пример.
Определитьвероятностьбезотказной работыизделия в течение1000 час, если
наработкадоотказаэтогоизделияподчиняетсягамма-распределениюспараметрамиα=4 иλ =10-3.
Решение:
Используемвыражениедлявероятностибезотказнойработы
P (t)=1− F (t)=
1− F (t)=1−
λα
Γ (α)
t
∫ tα −1 e − λtdt
0.
Длявычислениявыраженияможноиспользоватьтаблицыгамма-распределенияиликомпьютерныепрограммы.НижепоказанMathcad-документдлявычислениявероятности
𝛼:=4
t
𝛼- 1
:=10-3
-t
t:=1000
z𝛼
z:=t
0
e dt
y:=1-
𝛼
y=0.981
ВрезультатевычисленияполучимP(1000)=0,981=98,1%.
РаспределениеПуассона. Распределениеиспользуетсядлядискретныхслучайныхвеличин.Описываетпоявлениевнезапныхотказоввсложныхсистемахираспределениевременивосстановления,числоотказоводнотипногооборудованиязаопределенныйинтервалвремениит.п.
Функция распределения Пуассона для целочисленного аргумента m =0,1,2...
t
¿
λm − λ
¿ m!e
m ¿
∞
F (t)=∑
m =0
¿
| ∑ |
¿
¿
¿
| приt0. |
| . |
F (t)≡0при t ¿
¿
¿
Плотностьвероятностидискретногораспределения
λm
Pm (t)= m!
e − λ
,
гдеt-фиксированныйинтервалвремени,0.Чемменьшезначение,темассиметричнеераспределение.ПримерграфикадляраспределенияПуассона
показанна рис.22.График
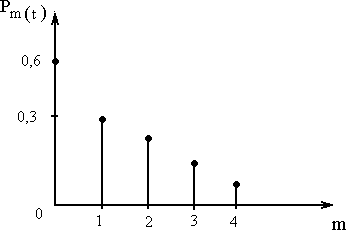построен дляλ= 0,5.
Суммавероятностей
∞
∑
m =0
Pm (t)=1
.
Математическоеожидание и дисперсияраспределенияПуассона
μ = M (t)= λ,
σ 2= D (t)= λ
.
Рис.22.
Лекция1.7Подготовкаинформациидляанализабезотказности
объектов.Подготовкаинформациидляанализабезотказностиобъектов