Определениепоказателейнадежности

1. Показателибезотказности

1.1 Вероятностьбезотказнойработы -вероятностьтого,чтовпределахзаданнойнаработкиtотказневозникает

P (t

N

)= p =

N

1− n ( t )

N,

гдеNр-числоработоспособныхобъектовнамоментt,N-общеечислонаблюдаемых объектов,

n(t)-числообъектов,отказавшихнамоментtотначалаиспытанийилиэксплуатации.

 

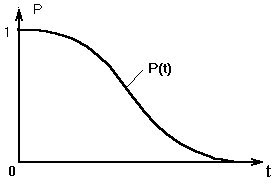
Рис.9.

Вероятностьбезотказнойработыуменьшаетсясувеличениемвремениработыилинаработкиобъекта.Зависимостьвероятностибезотказнойработыотвременихарактеризуетсякривойубылиресурсаобъекта,примеркоторойприведен нарис.9.

Вначальныймоментвременидляработоспособногообъектавероятностьегобезотказнойработыравнаединице

(100%).Помереработыобъектаэтавероятностьснижаетсяистремитсякнулю.

Вероятность отказа характеризуется вероятностью возникновенияотказа намоментвремениt

Q (t)=1− P (t)= n (t)

N,

гдеn(t)-числообъектов,отказавшихнамоментtотначалаиспытанийилиэксплуатации,

 

 

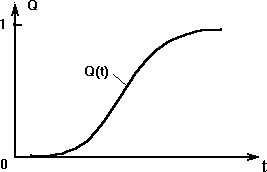
Рис.10.

N-общеечислонаблюдаемыхобъектов.

Вероятностьвозникновенияотказаобъектавозрастаетсувеличениемсрокаэксплуатацииилинаработки.

Пример зависимостивероятности возникновения отказаот времени показан на рис. 10. Дляработоспособногообъектавначальныймоментвременивероятность отказа близка к нулю.Длятого,чтобыотказпроявился

объекту необходимо начать работать, при этом вероятность отказаувеличиваетсясувеличениемвремениистремитсякединице.

Вероятностьотказаможетбытьтакжеохарактеризованаплотностьювероятности отказа

f (t)= dQ

dt или

f (t)= Δn (t)

N ⋅ Δt,

где Δn (t) -числоотказовзапромежутоквремениΔt,

N-общеечислонаблюдаемыхобъектов.

Пример 1. После 500 часов наработки из 56 агрегатов, поставленных наэксплуатацию,вработоспособномсостоянииоказалось43агрегата.Определитьвероятностьбезотказнойработыагрегатавтечение500час.

Решение:

Используем формулу для определения вероятности безотказной работыобъекта

P (500)= 43 =0,768

56.

Вероятностьбезотказнойработыагрегатавтечение500чассоставляет76,8

%.

Пример2.Дляпредыдущегопримераопределитьвероятностьотказаагрегат за500 часработы.

Решение:

Используемформулудлявероятностиотказа

Q (500)=1− P (500)=1−0,786=0,232

или

Q (500)= 56−43 =0,232

56.

Такимобразом,вероятностьотказаагрегатаза500чассоставляет23,2%.

 

Приопределениивероятностибезотказнойработыивероятностиотказовширокоиспользуютсядвеосновныхтеоремыдляопределениявероятности случайного события:

1. Вероятность появления одного из двух несовместных событий равнасуммевероятностиэтих событий

P (A + B)= P (A)+ P (B),

гдеA,B–несовместныесобытия.

2. Вероятностьсовместногопоявлениянесколькихнезависимыхсобытийравнапроизведениювероятностейэтихсобытий

P (A 1 A 2... An)= P (A 1)⋅ P (A 2)⋅...⋅ P (An).

Первая теорема используется для нахождения вероятности отказа привозможностиуобъектанесколькихвидовнесовместныхотказов.Сиспользованиемвторойтеоремыопределяютвероятностьбезотказнойработыобъекта, состоящего из многих элементов, вероятность безотказной работыкоторыхизвестна.

Пример3.Системасостоитих4-хагрегатов.Надежностькаждогоагрегатавтечениевремениtхарактеризуетсявероятностьюбезотказнойработы90%.Найтивероятностьбезотказнойработысистемывтечениевремениtприусловиинезависимостиотказов агрегатов.

Решение:

Используем теорему вероятности совместного появленияработоспособного состояния всехагрегатов

n 4

Pc (t)=∏ Pi (t)=∏0,9=0,656

i =1

i =1.

Следовательно,вероятностьбезотказнойработысистемывтечениевремениt равна65,6 %.

Пример4.В составе агрегата имеются5узлов.Вероятностьотказакаждого узла в течение времени t составляет 5 %. Отказы узлов несовместны.Определитьвероятностьотказаагрегата.

Решение:

Используемтеоремудлявероятностихотябыодногоизнесколькихнесовместных событий

n 5

Q (t)=∑ Qi (t)=∑0,05=0,25

i =1

i =1.

Такимобразом,вероятностьотказаагрегатавтечениевремени tсоставляет25 %.

1.2 Интенсивностьотказов -характеризуетскоростьвозникновенияотказовобъектавразличные моментывремениегоработы

λ (t)= Δn (t)

Nр ⋅ Δt,

гдеn(t)-числоотказовзапромежутоквремениt,Nр-числоработоспособныхобъектовнамоментt.

Интенсивностьотказовможетбытьнайденатеоретически

λ (t)= f (t)

P (t),

гдеf(t)-функцияплотностивероятностинаработкидоотказа,P(t)-вероятностьбезотказнойработы,

f (t)= Δn (t)

N ⋅ Δt.

Плотностьраспределенияf(t)наработкидоотказаможетбытьтакжеопределенаповероятностиотказа

f (t)= Q^' (t)= dQ (t)

dt или

t

Q (t)=∫ f (t) dt

0.

Вероятностьбезотказнойработысвязанасинтенсивностьюотказоводнимиз основныхуравненийтеориинадежности:

t

P (t)=exp(−∫ λ (t) dt)

0.

В описанных способах оценки безотказности до первого отказа отказынеразличаютсяпотяжестиихпоследствий.Вбольшинствеслучаевприразработкеобъектанеобходимоустановитькритерийотказаизделияпоэкономическимсоображением,исчерпаниюресурсаилидругимхарактеристикам.

Критериемотказа называютпризнакилисовокупностьпризнаковнеработоспособногосостоянияобъекта,установленныхвнормативно-техническойиликонструкторскойдокументации.

1.3 Средняянаработканаотказ -этоотношениенаработкивосстанавливаемого объекта к математическому ожиданию числа его отказоввтечениеэтойнаработки

N

∑ ti

=

T

i =1

o N

∑ mi

i =1,

где N - общее число объектов, поставленных на испытания или вэксплуатацию,t_i -наработкаi-того объекта,

m_i-числоотказовi-тогообъектазавесьнаблюдаемыйпериод.

Средняя наработка на отказ используется для характеристикивосстанавливаемыхобъектов.

1.4 Средняянаработкадоотказа -математическоеожиданиенаработкиобъектадо первого отказа

 

Tср

∞

=∫ P (t

 

) dt

 

или

¿ kΔt ¿¿

i

,

гдеN_pi-числоработоспособныхобъектовнаинтерваленаработки t_i–t_i+1;N-общее числонаблюдаемыхобъектов,

t=t_i+1-t_i-интервалвремени;

k-числорассматриваемыхинтерваловнаработки.

Среднююнаработкудоотказаможнотакжеопределитьиначе

1 n

Tcp = n ∑ ti,

гдеt_i-наработкадоотказаi-тогообъекта,n-числообъектов.

Показательиспользуетсядляхарактеристикинадежностиневосстанавливаемыхобъектов.

1.5 Средняянаработкамеждуотказами -математическоеожиданиенаработкиобъектаотокончаниявосстановленияегоработоспособногосостоянияпослеотказадовозникновенияследующегоотказа.

Вычисляетсякакотношениесуммарнойнаработкиобъектамеждуотказамизарассматриваемыйпериодкчислуотказовзатотжепериод

1 m

m

T = ∑ tii =1.

Показателибезотказностиопределяютнаразныхстадияхработыобъекта с целью его совершенствования и с целью контроля нормируемыхзначенийприэксплуатации.

 

2. Показателидолговечности

2.1 Среднийресурс -математическоеожиданиересурса

N

∑ Tpi

T = i =1

p N,

 

гдеТ_pi-ресурсi-тогообъекта,N-число объектов.

2.2 Гамма-процентныйресурс представляетсобойнаработку,втечениикоторойобъектнедостигаетпредельногосостояниясзаданнойвероятностью,выраженныйвпроцентах(рис. 11).

Длярасчетапоказателяиспользуетсяформулавероятности

P (Tpγ

∞

)=∫ p (T

Tpγ

) dTp = γ

,

p 100

гдеТ_pγ = наработкадопредельногосостояния(ресурс).

 

 

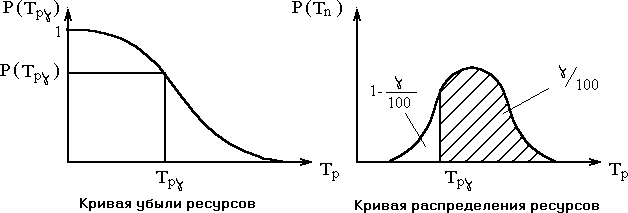
Рис.11.

Гамма-процентный ресурсявляетсяосновнымрасчетнымпоказателем

дляподшипниковидругихэлементов.

Существенноедостоинствоэтогопоказателя-возможностьегоопределениядозавершенияиспытаниявсехобразцов.Вбольшинствеслучаев используют90%ресурс.

2.3 Назначенный ресурс - суммарная наработка T_pн, при достижениикоторойприменениеобъектапоназначениюдолжнобытьпрекращенонезависимоотеготехнического состояния.

2.4 Установленныйресурс -техническиобоснованнаяилизаданнаявеличинаресурсаТ_ру,обеспечиваемаяконструкцией,технологиейи

эксплуатацией,впределахкоторойобъектнедолжендостигатьпредельногосостояния.

2.5 Среднийсрокслужбы -математическоеожиданиесрокаслужбы.

N

∑ Tслi

Tсл

= i =1

N,

гдеТ_слi-срокслужбыi-тогообъекта.

2.6 Гамма-процентныйсрокслужбы –календарнаяпродолжительностьэксплуатациивтечениекоторойобъектнедостигаетпредельногосостояниясвероятностьюγ,выраженнойвпроцентах

P (Tслγ ∞)=∫ p (T

Tслусл) dT = γ

.

сл 100

2.7 Назначенныйсрокслужбы -суммарнаякалендарнаяпродолжительность эксплуатации Т_сл.н, при достижении которой применениеобъектапоназначениюдолжнобытьпрекращено,независимоотеготехнического состояния.

2.8 Установленный срок службы – технико-экономически

обоснованныйилизаданныйсрокслужбыТ_сл.у,обеспечиваемыйконструкцией, технологией и эксплуатацией, в пределах которого объект недолжендостигать предельного состояния.

 

3. Показателисохраняемости

3.1 Среднийсроксохраняемости –математическоеожиданиесрокасохраняемостиобъекта

1 N

N,

Tc = ∑ Tcii =1

гдеТ_сi-сроксохраняемостиi-тогообъекта.

3.2 Гамма-процентныйсроксохраняемости -календарнаяпродолжительностьхраненияи(или)транспортированияобъекта,втеченииипослекоторойпоказателибезотказности,долговечностииремонтопригодностиобъектаневыйдутзаустановленныепределысвероятностьюγ, выраженнойвпроцентах

P (Tсγ _γ.∞)=∫ p (Tc

Tcγ) dT = γ c 100

,-выражениедлярасчетапоказателя_с

3.3 Назначенный срок хранения - календарная продолжительность Т_с.н.хранения в заданных условиях, по истечении которой применение объекта поназначениюнедопускается, независимоотего состояния.

3.4 Установленныйсроксохраняемости -технико-экономическиобоснованный(илизаданный)срокхраненияТ_с.у.,обеспечиваемыйконструкциейиэксплуатациейвпределахкоторогопоказателибезотказности,долговечности,ремонтопригодностиобъектасохраняютсятемиже,какимионибылиуобъектадоначалаегохраненияи(или)транспортирования.

 

4. Показателиремонтопригодности

4.1 Среднее время восстановления - математическое ожидание временивосстановления объекта

1 m

m,

Tв = ∑ Tвk

k =1

где Т_вк - время восстановления ķ-того отказа объекта, m - число отказов зазаданный срокиспытаний илиэксплуатации.

4.2 Вероятностьвосстановленияработоспособногосостояния -вероятность того, что объект будет восстановлен в заданное время tв. Длябольшинстваобъектовмашиностроениявероятностьвосстановленияподчиняетсяэкспоненциальномузаконураспределения

в

,

P (t)= e − λ ⋅ tв

где-интенсивностьотказов(принимаетсяпостоянной).

 

5. Комплексныепоказатели

5.1 КоэффициентготовностиК_г -вероятностьтого,чтообъектокажетсяработоспособнымвпроизвольныймоментвремени,кромепланируемыхпериодов,втечениекоторыхприменениеобъектапоназначениюнепредусматривается. Необходимо указывать интервал эксплуатации объекта,накоторомследуетоцениватькоэффициентготовностиК_г

N

∑ ti

K = i =1

г N N

∑ ti +∑ τi

i =1

i =1,

где t_i -суммарная наработка i-того объекта в заданном интервалеэксплуатации,

_i- суммарное время восстановления i-того объекта за тот же период эксплуатации,

N-числонаблюдаемыхобъектоввзаданноминтервалеэксплуатации.

ЕслиназаданноминтервалеэксплуатацииопределенысреднеезначениенаработкинаотказТ_оисреднеевремявосстановленияобъектапослеотказаТ_в, то

K = Tо

 

T

+ T

г

о

в.

5.2 Коэффициенттехническогоиспользования -отношениематематическогоожиданиянаработкиобъектазанекоторыйпериодэксплуатацииксуммематематическихожиданийнаработки,продолжительноститехническогообслуживания,плановыхремонтовинеплановыхвосстановленийзатотжепериодэксплуатации

K = Tо

 

т. и

Tо + τ

т. о + τ

p + Tв.

5.3 Коэффициент оперативнойготовности - вероятность того, чтообъект окажется работоспособным в произвольный момент времени, кромепланируемыхпериодов,втечениекоторыхприменениеобъектапоназначению не предусмотрено, и, начиная с этого момента, объект будетработатьбезотказновтечениизаданногоинтервалавремени

Kог = Kг ⋅ P (t 0 ,t 1),

где Р (t₀, t₁) - вероятность безотказной работы объекта в интервале (t₀, t₁),t₀ -моментвремени,скотороговозникаетнеобходимостьпримененияобъектапоназначению, t₁- момент времени, когда применение объекта по назначениюпрекращается.

Коэффициент К_гопределяют для периода ожидания работы,

предшествующегомоментуt_o.

 

Лекция3.Математическаямодельнадежностиобъекта.

Показателинадежностиопределяютсянаосновеспециальныхиспытанийобъектовнанадежностьилиподаннымпрактическойэксплуатацииобъектов.Результатытакихиспытанийилиэксплуатацииявляютсястатистическимиданными,которыеможнорассматриватькаквыборку случайной величины. Для этой выборки можно найти выборочныеоценки математического ожидания и дисперсии случайной величины. Крометого, необходимо определить закон распределения случайной величины инайти наиболее близкий вид функции распределения случайной величиныилиплотностьвероятности.

Ввыборкевсегдабудетконечноечислонаблюдений,чтодаетвозможность лишь оценить значение показателей надежности. Пусть впроцессеэкспериментаполученоnнаблюденийслучайнойвеличиных: Χ (x 1 ,x 2 ,x 3... xn).Наоснованииэтихнаблюденийопределяется

некоторыйпоказательнадежности

m ^, который будет являться оценкой

фактической(теоретической)величиныпоказателяm:

m ^≈ m.

Можно указать определенную вероятность γ того, что оценкаотличаетсяотфактическогозначениянеболеечемнавеличинупогрешности



γ = P (∣ m ^− m ∣≤ Δ),

где-допустимаяпогрешность, γ-достоверностьоценки.

• Оценка m ^ называется несмещенной, если ее математическое

ожидание совпадаетсфактическим значением параметра M (m ^)= m.

• Оценка m ^ называется состоятельной, если при увеличении числа

наблюденийnдобесконечностиоценкасходитсякоцениваемомупараметруповероятности.

• Оценка, обладающая наименьшей дисперсией, называется

эффективной.

Приопределенииоценки m ^

частотребуетсяопределитьнадежность

этойоценкииееточность.Сэтойцельювматематическойстатистикеиспользуются доверительныеинтервалы и доверительныевероятности.

 

 

Доверительныминтервалом J_γпараметраmназываетсяслучайный

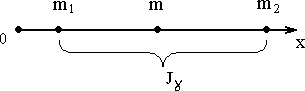интервалm₁...m₂,которыйнакрываетистинноезначениепараметра m с вероятностью γ.Величинаγназываетсядоверительной вероятностью, авеличины m₁и m₂

 

Рис.23.

доверительнымиграницами.Графическаяинтерпретациядоверительногоинтервала представлена нарис. 23, гдеm₁- нижняя доверительная граница,m₂- верхняядоверительнаяграница.

Ширина интервала характеризует точность оценки параметра

γ =¿ P (mн ≤ m ^≤ mв)

¿. Истинное значение параметра

m = m ^± ε

. Если

величинаmподчиняетсянормальномузаконураспределения,тонижняядоверительнаяграницаиверхняядоверительная граница

mн = m ^− z

σ

γ √ n,

mв = m ^+ z

σ

γ √ n,

гдеσ-стандартноеотклонение, z_γ-коэффициентдлядоверительнойвероятности γ,определяемыйпотаблицам,n-числонаблюдений.

Есливеличинастандартногоотклоненияσнеизвестна,товместонееиспользует сявыборочноест андартное отклонение

s =

∑(m − m)2

m

= m ^− t

σ

m

= m ^+ t

σ

n −1 i =1

i

,

н

γ √ n,

в

γ √ n,

√ 1 n ¿

где t_γ - табличный коэффициент, определяемый для заданной доверительнойвероятностиγпочислустепеней свободык=n –1.

Дляоценкизаконараспределенияслучайнойвеличиныприэкспериментальномееизучениивыдвигаютипроверяютстатистическуюгипотезуосоответствиинаблюдаемогораспределениянекоторомутеоретическомураспределению.

Оценкаверностиилиневерностигипотезыпроизводитсясиспользованиемнекоторогокритерия.ЧастодляэтойцелииспользуетсякритерийсогласияПирсона χ 2(критерийхи-квадрат).

Пустьврезультатеnнезависимыхнаблюденийопределяласьчастота

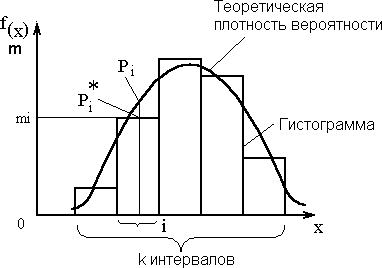попаданийm_iслучайнойвеличиныводинизинтерваловi,приобщемчислеинтерваловkипорезультатамнаблюденийпостроенагистограмма(рис.24).

Тогда по видугистограммы можнопредположитьсправедливость дляраспределенияслучайнойвеличины одного изтиповых законов, что

Рис.24.

позволяет вычислить

теоретическое значение P_i для плотности вероятности случайной величины,соответствующей серединеинтервалаi.

ИспользуятеоретическиезначенияплотностивероятностиP_iинаблюдаемоечислоm_iпопаданийслучайнойвеличинывинтервалi,вычисляют критерий согласияПирсона

^k (m − n ⋅ P)²

χ ²=∑

i =1

i i

n ⋅ Pi,

гдеm_i - числозначенийвеличиныХвинтервалеi;P_i-теоретическаявероятность появления случайной величины Х, имеющей значение равноесерединеинтервала;n-общеечислонаблюдений,k-числоинтерваловзначенийслучайнойвеличины.

Вычисленноепоформулезначениекоэффициента χ 2сравниваетсяс

критическим значением коэффициента, который зависит от числа степенейсвободыrиопределяетсяпостатистическим таблицам,

r = k − s,

где s - число независимых условий (связей), наложенных на частоты P_i*.Числосвязейsравночислупараметровоцениваемогораспределенияплюс1.Например,еслиоцениваетсянормальноераспределение(характеризуемоедвумяпараметрамиμиσ), то s =2 +1 =3.

Еслирасчетноезначениенепревосходиткритическоезначениекритерия χ 2тогипотезаосправедливостипринятоготеоретическогораспределенияпринимается.Впротивномслучаенеобходимоподобратьдругойзаконраспределенияслучайной величины.