(вопрос 9)
Закон сохранения импульса (ЗСИ): в замкнутой системе полный импульс остается постоянным
или
где 
– массы тел, входящих в систему; 
– скорости соответствующих тел до взаимодействия; 
– скорости этих же тел после взаимодействия.
Замкнутой механической системой является такая система тел, на которую не действуют внешние силы. Но таких идеальных систем на практике не встречается: невозможно создать такую систему, чтобы полностью исключить ее взаимодействие с внешними телами, не входящими в систему. При решении практических задач замкнутой системой тел можно считать такую, на которую действуют внешние силы, но их сумма равна нулю. В ряде задач сохраняется проекция импульса на одну из осей, если при этом проекции внешних сил на эту ось равны нулю.
 |
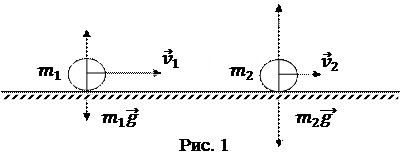Пример практически замкнутой системы приведен на рис. 1. На тела, входящие в систему: на два шарика, движущихся вдоль оси x, – действуют силы тяжести 
и силы нормальных реакций опоры 
но сумма этих сил равна нулю, да и проекции их на направление скорости равны нулю.
Закон сохранения момента импульса
(вопрос 11)
Закон сохранения момента импульса (ЗСМИ) можно применять к любой механической системе при условии, что результирующий момент всех внешних сил, приложенных к системе, равен нулю 
. Формулировка закона: Момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени:
.
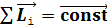Здесь записана сумма векторов моментов импульса всех частей системы.
Напомним, что момент импульса твердого тела равен произведению его момента инерции на угловую скорость: 
, – а момент импульса системы тел есть векторная сумма моментов импульса всех тел данной системы:
.
Закон сохранения механической энергии
(вопрос 15)
Закон сохранения механической энергии (ЗСМЭ ): полная механическая энергия системы тел сохраняется, если на тела системы действуют только консервативные силы (внутри и извне), а диссипативные силы отсутствуют или их работа равна нулю:
,
где 
– кинетическая энергия, равная сумме энергий всех тел системы,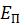 
– потенциальная энергия системы.
Консервативными являются силы, работа которых зависит только от закона сил и от начального и конечного положения тела; работа консервативных сил равна убыли потенциальной энергии системы. Консервативными являются сила тяжести, сила упругости 
гравитационная сила. Диссипативными являются силы трения и сопротивления, приводящие к превращению механической энергии во внутреннюю энергию тел путем их нагрева.
ЗСМЭ является частным случаем закона сохранения энергии системы: вследствие действия диссипативных сил происходит превращение кинетической энергии тел в эквивалентное количество других видов энергии, не связанных с механическим движением тел, например, в энергию теплового движения молекул.
Механические колебания
(вопрос 20, 22)
Гармонические колебания описывают уравнением:
,
где x – смещение колеблющейся точки относительно положения равновесия в момент времени t; 
– наибольшее смещение, или амплитуда колебаний; w – циклическая частота колебаний; j0 – начальная фаза колебаний; 
– фаза колебаний в момент времени t.
Колебания характеризуют частотой w и периодом T, связанными друг с другом соотношением: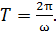 
Период колебаний математического маятника
,
где 
– длина маятника; 
– ускорение свободного падения.
Период колебаний пружинного маятника
,
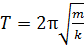где m – масса груза; k – жесткость пружины.
Кинетическая энергия гармонических колебаний
,
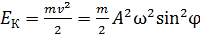где m – масса колеблющегося объекта; 
– его скорость.
Потенциальная энергия гармонических колебаний
,
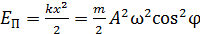где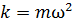 
– жесткость, или коэффициент упругости пружины.
(вопрос 21)
Результатом сложения одинаково направленных гармонических колебаний равной частоты является также гармоническое колебание с периодом, равным периоду складываемых колебаний. Если уравнения двух складываемых колебаний:
,
,
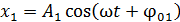то уравнение результирующего колебания:
.
Здесь амплитуда результирующего колебания
,
где 
– амплитуды складываемых колебаний;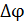 
– их разность фаз.
(вопрос 23)
Уравнение затухающего колебательного движения имеет вид
.
Здесь 
является амплитудой затухающих колебаний;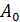 
–начальная амплитуда (в момент времени 
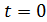); d – коэффициент затухания, его величина 
, где r – коэффициент сопротивления среды; m – масса колеблющейся точки. Затухание колебаний характеризуют логарифмическим декрементом затухания
,
где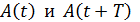 
– амплитуды двух последовательных колебаний, отделенных друг от друга периодом колебаний T.
Циклическая частота затухающих колебаний
,
где 
– циклическая частота свободных (собственных) незатухающих колебаний той же колебательной системы.