Системы линейных уравнений

Программа экзамена по курсу «Алгебра и геометрия»

Семестр

Экзамен будет проходить в 2 этапа:

1 этап. Тестирование – 16 баллов (15 заданий).

Оценивание:

8 правильных ответов - 2 балла; 9 правильных ответов - 4 балла; 10 – 6 баллов; …….;

15 правильных ответов – 16 баллов.

 

При получении 10 баллов допускается прохождение 2-го этапа экзамена.

2 этап. Устный ответ и решение задач повышенной сложности – 24 балла (3 задания).

Оценивание: 8 баллов за каждое задание.

 

1. Матрицы и операции над ними (сложение, умножение на число, произведение, транспонирование). Свойства операций. Перестановочные матрицы.

2. Системы линейных уравнений (основные определения). Метод Гаусса.

3. Перестановки степени n. Четность перестановки. Транспозиция.

4. Определение определителя. Определители 2-го и 3–го порядков. Определитель треугольной матрицы

5. Основные свойства определителя.

6. Миноры. Алгебраические дополнения. Теорема о разложении определителя по строке (столбцу).

7. Определитель с углом нулей. Теорема об определителе произведения матриц.

8. Обратная матрица. Критерий существования обратной матрицы. Свойства обратной матрицы.

9. Линейная зависимость и линейная независимость систем строк. Свойства систем строк.

10. Теорема о двух системах строк.

11. Теорема о базисах.

12. Теорема о ранге матрицы. Вычисление ранга матрицы путем приведения к ступенчатому виду. Перечислить основные этапы обоснования.

13. Ранг произведения матриц.

14. Теорема Кронекера-Капелли.

15. Фундаментальная система решений. Теорема о числе решений в ФСР однородной СЛУ.

16. Понятие вектора. Коллинеарные, компланарные векторы. Операции над векторами и их свойства.

17. Скалярное произведение векторов, его свойства и способы вычислений.

18. Векторное произведение векторов и его свойства.

19. Смешанное произведение векторов и его свойства.

20. Деление отрезка в данном отношении.

21. Прямая на плоскости, виды уравнений прямой на плоскости.

22. Взаимное расположение прямых на плоскости. Угол между прямыми. Расстояние от точки до прямой.

23. Уравнение плоскости. Уравнение прямой в пространстве.

24. Взаимное расположение плоскостей, прямой и плоскости в пространстве. Угол между плоскостями. Угол между прямой и плоскостью.

25. Расстояние от точки до плоскости, от точки до прямой в пространстве, между скрещивающимися прямыми.

 

 

Примеры задач

Системы линейных уравнений

1. Заданная система линейных уравнений имеет матрицу коэффициентов:

Известно, что |A| = 0. Тогда указанная система линейных уравнений:

(а) совместна;

(б) несовместна;

(в) ничего определенного о ее совместности сказать нельзя.
Выбрать правильный ответ. Выбор обосновать.

1. Какие из следующих утверждений неверны:

(а) Если определитель квадратной системы линейных уравнений равен нулю, то система линейных уравнений не
имеет решений;

(б) Если определитель квадратной системы линейных уравнений не равен нулю, то система линейных уравнений
совместна;

(в) Если определитель квадратной системы линейных уравнений равен нулю, то система линейных уравнений имеет
более одного решения;

(г) Если определитель квадратной системы линейных уравнений не равен нулю, то система линейных уравнений
определена?

Ответ обосновать.

1. Если ранг матрицы коэффициентов однородной системы линейных уравнений на единицу меньше числа неизвестных, то любые два решения этой системы пропорциональны. Доказать.
2. Пусть a ₁, a ₂, a ₃ — произвольные решения неоднородной системы линейных уравнений. Доказать, что 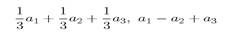— решения этой же системы линейных уравнений. При каких условиях на коэффициенты данная линейная комбинация

любых решений a ₁, a ₂,..., a_m неоднородной системы линейных уравнений снова будет решением этой системы?

1. Пусть задана система линейных уравнений, в которой число уравнений на единицу больше числа неизвестных. Доказать, что если эта система совместна, то определитель ее расширенной матрицы равен нулю.

 

Линейная зависимость

1. Указать, какие из сформулированных ниже утверждений верны.
   Система a ₁, a ₂,..., a_n линейно зависима тогда и только тогда, когда

(а) существует тривиальная линейная комбинация этой системы, равная нулю;

(б) существует нетривиальная линейная комбинация этой системы, равная нулю;

(в) любая нетривиальная линейная комбинация этой системы равна нулю;

(г) если существует нетривиальная линейная комбинация этой системы, не равная нулю.

1. Указать, какие из сформулированных ниже утверждений верны.
   Система a ₁, a ₂,..., a_n линейно независима, тогда и только тогда, когда

(а) любая линейная комбинация этой системы тривиальна;

(б) любая линейная комбинация этой системы, не равная нулю, тривиальна;

(в) любая линейная комбинация этой системы, равная нулю, тривиальна;

(г) любая нетривиальная линейная комбинация этой системы равна нулю.

1. Известно, что 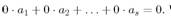Что можно сказать о системе a ₁, a ₂,..., a _s?
2. Даны две системы строк:

Известно, что первая система линейно независима и каждая ее строка выражается через вторую систему. Тогда

(а) m≥ 15;

(б) m < 15;

(в) m может быть как меньше 15, так и больше 15.
Выбрать правильный вариант. Ответ обосновать.

1. Даны три системы строк

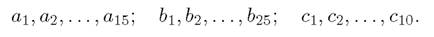
Известно, что первая выражается через вторую, а вторая — через третью.

Тогда первая система строк

(а) линейно зависима;

(б) линейно независима;

(в) может быть как линейно зависимой, так и линейно независимой.

1. Известно, что . Доказать, что a ₄ выражается через a, a ₂, a ₃.
2. Построить векторы a, a ₂, a ₃ так, чтобы

(а) rank (a, a ₂, a ₃) = 2, rank (a, a ₂) = rank (a ₂, a ₃) = 1;

(б) rank (a, a ₂, a ₃) = 2, rank (a, a ₂) = rank (a ₂, a ₃) = rank (a, a ₃) = 1.

1. Даны четыре строки

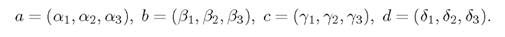
Известно, что строка d не выражается через a, b, с. Тогда система a, b, с

(а) линейно независима;

(б) линейно зависима;

(в) ничего определенного о линейной зависимости этой системы сказать нельзя.
Выбрать правильный вариант, ответ обосновать.

1. Дана система строк

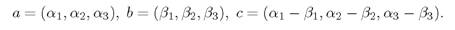
Доказать, что найдется строка d = (s₁,s₂,s₃), которая не выражается через a, b, с.

1. Доказать, что если три вектора a, b, с линейно зависимы и вектор с не выражается линейно через векторы a и b, то векторы a и b, различаются между собой лишь числовым множителем.
2. Система векторов a, b, с линейно независима. Доказать, что если вектор b выражается через каждую подсистему этой системы из двух векторов, то b = 0.
3. Дана линейно зависимая система из трех векторов a, b, с ∈ R³. Доказать, что найдется строка d ∈ R³, которая не выражается через систему строк a, b, с.
4. В каком случае система векторов обладает единственным базисом?
5. Привести пример системы из трех строк, который опровергает следующее утверждение: Если некоторая система из n строк линейно зависима, то в ней найдется линейно зависимая подсистема из n - 1 строк.

 

Перестановки

1. В перестановке (i₁, i₂,..., i_n) имеется k инверсий. Сколько инверсий имеется в перестановке (i_n, i_n-1,...,i₂, i₁)?
2. Сколько инверсий образует число 1, стоящее на k -ом месте перестановки?
3. Сколько инверсий образует число n, стоящее на k -ом месте в перестановке чисел 1, 2, 3,..., n?
4. Чтобы получить одну нечетную перестановку из другой нечетной потребуется не менее двух транспозиций. Доказать.
5. Привести пример таких двух нечетных перестановок, что одну из другой нельзя получить с помощью двух транспозиций. Доказать, что в этом случае для этого требуется не менее четырех транспозиций.
6. Даны две перестановки различной четности. Доказать, что если одну из другой нельзя получить с помощью одной транспозиции, то для получения одной из другой потребуется не менее трех транспозиций.
7. Сколько различных перестановок можно получить из данной перестановки степени n путем применения ровно одной транспозиции. Тот же вопрос для транспозиций соседних элементов.

 

Определитель

1. Пусть A — квадратная матрица второго порядка, B — квадратная матрица третьего порядка. Выразить следующие определители через определители матриц A и B:

1. Определитель 4-го порядка во второй строке имеет элементы x₁, x₂, x₃, x₄. Некто разложил этот определитель по элементам названной строки: 2x₁ + 3x₂ + 4x₃ + 5x₄.

Найти дополнительные миноры к элементам второй строки.

1. Некто вычислил дополнительные миноры к элементам второй строки определителя 4-го порядка: 1, 2, 3, 4. Элементы третьей строки этого определителя равны: a, b, c, d. Вычислить -a + 2b - 3c + 4d.
2. Вычислить

1. Известно, что квадратные матрицы A, B целочисленные и C = AB, С = 10. Найти |A|, |B|, если все элементы второго столбца матрицы A четны, элементы третьей строки B делятся на 5 и оба определителя положительны.
2. Все элементы определителя 3-го порядка равны ±1, то сам определитель будет четным числом. Доказать.
3. Все элементы определителя 4-го порядка равны ±1, то сам определитель будет делиться на 8. Доказать.
4. Вычислить определитель порядка n, элементы которого заданы условиями a_ij = min(i, j).
5. Вычислить определитель порядка n, элементы которого заданы условиями a_ij = max(i,j).
6. Выписать все члены определителя 4-го порядка, входящие в него со знаком минус.
7. Выписать все члены определителя 4-го порядка, которые содержат ровно один элемент главной диагонали. Определить их знаки.
8. Выписать все члены определителя 4-го порядка, которые содержат ровно два элемента главной диагонали. Определить их знаки.
9. Выписать все члены определителя 4-го порядка, которые не содержат ни одного элемента главной диагонали. Определить их знаки.

 

1. Доказать, что определитель

где a _ij ∈ Z, является целым нечетным числом.

1. Доказать, что определитель

где aij ∈ Z, является целым нечетным числом.

1. Вычислить определитель

 

1. Что можно сказать об определителе, у которого сумма строк с нечетными номерами равна сумме строк с четными номерами?

 

Действия с матрицами

1. Матрицы A, B, C D таковы, что выражение AB + BC + CD имеет смысл. Доказать, что A и D — квадратные матрицы.
2. Матрицы A, B, C обратимы. Найти матрицу, обратную к произведению ABC^-1.
3. Три квадратные матрицы обладают свойством ABC = E. Обратима ли B? Если да, то указать обратную.
4. Матрица А называется ортогональной, если транспонированная к A матрица совпадает с обратной к A. Доказать, что определитель ортогональной матрицы равен ±1.
5. Квадратная матрица A называется симметричной, если a _ij = a _ji для любых i,j. Известно, что матрицы A, B симметричны. Будут ли симметричными матрицы: AB, ABA? Ответ обосновать.
6. Квадратная матрица A называется симметричной, если a _ij = a _ji для любых i,j. Доказать, что произведение двух симметричных матриц тогда и только тогда будет симметричной матрицей, когда данные матрицы перестановочны.
7. Как изменится произведение AB матриц A и B, если переставить i-й и j-й столбцы матрицы B?
8. Вычислить выражение

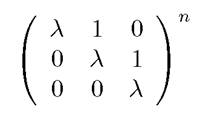
1. Дана матрица

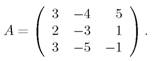
Какие из следующих матриц являются обратными к А:

 

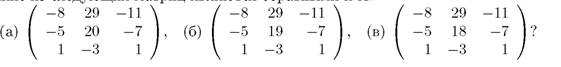
1. Доказать, что любая матрица, перестановочная с заданной матрицей А, симметрична. Здесь

 

 

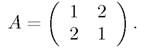
Ранг матрицы

1. Известно, что 7×7-матрица A имеет ранг 5. Найти ранг присоединенной матрицы A*.
2. Доказать, что если все миноры порядка 3 матрицы A равны нулю, то все ее миноры 4-го порядка тоже равны нулю.
3. Известно, что rank A = 2, rank B = 1. Какие из указанных ниже равенств невозможны:
   (a) rank AB = 3, (б) rank AB = 2, (в) rank AB = 1, (г) rank AB = 0?

Ответ обосновать.

1. Известно, что З×З-матрица A имеет ранг 3, а 3×10 матрица имеет ранг 2. Какие из указанных ниже равенств возможны:

(a) rank AB = 5, (б) rank AB = 3, (в) rank AB = 2, (г) rank AB = 1?

Ответ обосновать.

1. Доказать, что столбцы любой 7×9-матрицы A линейно зависимы.
2. Какие из следующих утверждений неверны (ответ обосновать): Если определитель квадратной матрицы A равен нулю, то

(а) A имеет пропорциональные строки;

(б) A имеет пропорциональные столбцы;

(в) строки A линейно зависимы;

(г) столбцы A линейно зависимы.
Ответ обосновать.

1. Столбцы квадратной матрицы A линейно зависимы. Что можно сказать о ее строках? Ответ обосновать.
2. Дана матрица

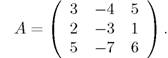
Вычислить произведение AА*, где A* — присоединенная к A матрица.

Обратима ли матрица A? Доказать, что AA* = 0 тогда и только тогда, когда |A| = 0.

 

 

Геометрия

62. Точки K и L служат серединами сторон BC и CD параллелограмма ABCD. Выразить векторы BC и CD через векторы AK и AL.

63. Дан тетраэдр O ABC. Выразить через векторы OA, OB, OC вектор EF, где E — середина ребра OA, a F — точка пересечения медиан треугольника ABC.

64. Даны векторы a = (2,5,14), b = (14,5,2). Найти проекцию вектора a на плоскость O xy при направлении проектирования, параллельному вектору b.

65. Вершина O тетраэдра O AB C принята за начало координат, а ребра O A, OB, OC — за базис. Найти координаты точек пересечения медиан граней тетраэдра.

66. Даны две точки A(-3, 1) и B(2, -3). На прямой AB найти точку M так, чтобы она была расположена по ту же сторону от точки A, что и точка B и чтобы отрезок AM был втрое больше отрезка AB.

67. Дана точка A(2,4). Найти точку при условии, что точка пересечения прямой A с осью ординат делит отрезок в отношении, равном 2/3, а точка D пересечения прямой с осью абсцисс делит отрезок AB в отношении -3/4.

68. Даны три вектора: a = (8,4,1), b = (2, -2,1), c = (1,1, 9). Найти вектор, являющийся ортогональной проекцией вектора c на плоскость, определяемую векторами a и b.

69. Даны два вектора: a = (8, 4,1), b = (2, -2,1). Найти вектор c, компланарный векторам a и b, перпендикулярный вектору a, равный ему по длине и образующий с вектором b тупой угол.

70. Вычислить объем тетраэдра ABCD, если A(2,-1,1), B(5, 5,4), C(3, 2, -1) и D(4, 1,3).

71. Даны три вектора: a = (8, 4,1), b = (2, -2,1), c = (4,0, 3). Найти четвертый вектор d длины 1, перпендикулярный к векторам a и b и направленный так, чтобы упорядоченные тройки векторов a, b, c и a, b, d имели одинаковую ориентацию.

72. Через точку M(2, 5) провести прямую, равноудаленную от точек P( - 1,2) и Q(5, 4).

73. Найти касательные к окружности с центром (1,1) и радиусом 3, параллельные прямой 5x - 12y = 0.

74. Составить уравнение плоскости, проходящей через прямую x = 2 + 3t, y = - 1 + 6t, z = 4t и параллельной прямой x = - 1 + 2 t, y = 3t, z = -t.

75. Составить уравнение прямой, если она лежит в плоскости y + 2z = 0 и пересекает прямые x = 2 - t, y = 4 + 2t, z = 1 и x=1- t, y = t, z = 6 + t.

76. Установить взаимное расположение прямой l и плоскости P. Если они пересекаются, найти точку их пересечения.

l: (x - 13)/8 = (y - 1)/2 =(z- 4)/3; P: x + 2y - 4z + 1 = 0.

77. Установить взаимное расположение двух прямых. Если они пересекаются или параллельны, написать уравнение плоскости, которая их содержит:

x = 1 + 9t, y = 2 + 6t, z = 3 + 3t; x = 7 + 6t, y = 6 + 4t, z = 5 + 2 t.

78. Найти расстояние от точки (1, 3, 5) до прямой: x = t, y = 1 - 2 t, z = 3 + t.

79. Найти расстояние между двумя прямыми: x = 3t, y = 1 - t, z = 2 + 2 t; x = -t, y = 2 + 3t, z = 3t.