В результате 30 измерений случайной величины Х при одинаковых условиях получены данные, записанные в таблице
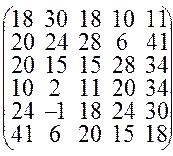 |
.
По выборочным данным требуется:
1) Разбить элементы выборки на 7 равных промежутков, составить статистический ряд распределения;
2) Построить гистограмму частот, графики выборочной плотности 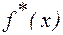 и выборочной функции распределения
и выборочной функции распределения 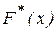 ;
;
3) Найти выборочное среднее 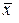 , выборочную дисперсию
, выборочную дисперсию 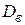 и исправленное выборочное среднее квадратичное отклонение S;
и исправленное выборочное среднее квадратичное отклонение S;
4) Записать теоретическую плотность распределения f(x), предполагая нормальное распределение Х, построить её график вместе с графиком эмпирической плотности распределения 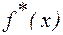 .
.
Оценить согласованность нормального распределения с выборочными данными, используя критерий Пирсона или Романовского. В случае согласованности выборочных данных с нормальным распределением найти доверительные интервалы для М(Х) и s(Х);
5) Предполагая равномерное распределение Х найти его параметры и записать плотность распределения f(x), оценить его согласованность с выборочными данными;
6) Среди рассмотренных распределений (нормального и
равномерного) выбрать лучшее согласование с выборкой,
с его помощью найти вероятность попадания Х в промежуток
от 10 до 20.
Решение:
1) Составим распределение выборки.
1.1) Упорядочим по возрастанию элементы выборки
и получим ранжированный ряд:
–1; 2; 6; 6; 10; 10; 11; 11; 15; 15; 15; 18; 18; 18; 18;
20; 20; 20; 20; 24; 24; 24; 28; 28; 30; 30; 34; 34; 41; 41.
Объем выборки n =30 (количество элементов).
1.2) Среди элементов выборки имеются повторяющиеся, составим
вариационный ряд (таблица 1), где каждой варианте 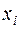 указана её
указана её
частота 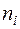
Таблица 1
Варианты 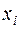
| -1 | ||||||||||||
Частоты 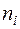
|
1.3) Составим интервальное распределение выборки.
Существует несколько способов составления интервального ряда с различными результатами.
Основной способ: При 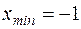 ,
, 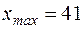 получим размах выборки
получим размах выборки 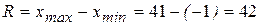 . Число равных интервалов по условию k =7, найдем шаг разбиения
. Число равных интервалов по условию k =7, найдем шаг разбиения 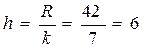 . Распределив 30 элементов выборки на 7 равных промежутков, получим интервальный статистический ряд (таблица 2).
. Распределив 30 элементов выборки на 7 равных промежутков, получим интервальный статистический ряд (таблица 2).
Таблица 2
| Номер i | |||||||
| Границы промежутка | (-1; 5) | (5;11) | (11;17) | (17;23) | (23;29) | (29;35) | (35;41) |
| Середина xio | |||||||
| Частота ni | |||||||
Относительные частоты 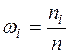
| 0.067 | 0.167 | 0.133 | 0.267 | 0.167 | 0.133 | 0.067 |
| Относительные частоты (%) | 6,7 | 16,7 | 13,3 | 26,7 | 16,3 | 13,3 | 6,7 |
При этом варианта х =11 попала на границу второго и третьего промежутков, её частоту (2) распределили поровну между этими промежутками
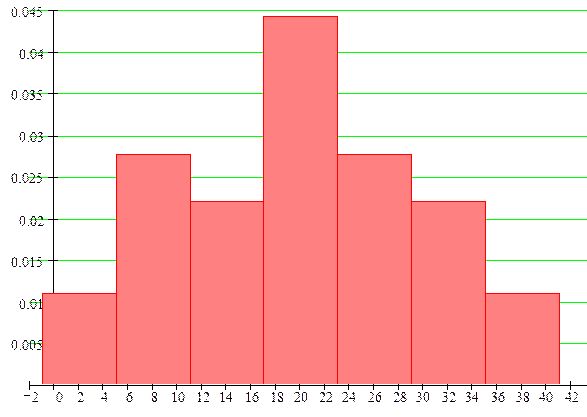
Пользуясь интервальным распределением выборки (таблица 2) построим гистограмму частот (рисунок 1).
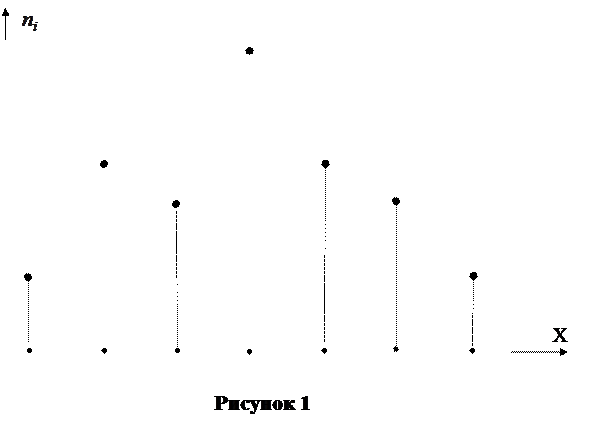
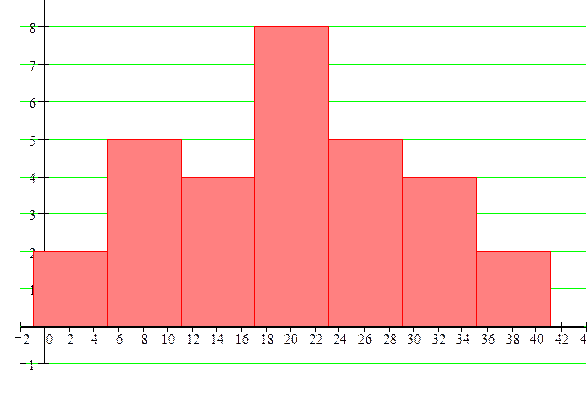
Для построения гистограммы относительных частот берут высоты прямоугольников на каждом промежутке равными относительной частоте 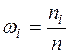 соответствующего промежутка. При этом гистограмма относительных частот отличается от гистограммы частот только масштабом по оси
соответствующего промежутка. При этом гистограмма относительных частот отличается от гистограммы частот только масштабом по оси 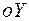 , где значения получены из
, где значения получены из 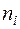 делением на постоянное число
делением на постоянное число 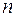 .
.
Иногда попадающую на границу двух промежутков варианту учитывают только в правом промежутке со всей её частотой, тогда в интервальном ряде могли получить 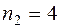 ,
, 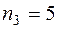 . При этом получим иной интервальный ряд (таблица 3), изменятся гистограммы частот и относительных частот.
. При этом получим иной интервальный ряд (таблица 3), изменятся гистограммы частот и относительных частот.
Таблица 3
| Номер i | |||||||
| Границы промежутка | (-1; 5) | (5;11) | (11;17) | (17;23) | (23;29) | (29;35) | (35;41) |
| Середина xio | |||||||
| Частота ni |
2 способ: При небольшом числе промежутков 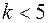 , допуская отклонения в обе стороны от наибольшего и наименьшего наблюдаемых, берут шаг
, допуская отклонения в обе стороны от наибольшего и наименьшего наблюдаемых, берут шаг 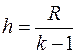 . Для первого промежутка отступают от
. Для первого промежутка отступают от 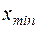 на половину шага влевои вправо, для последнего на половину шага вправо и влево от
на половину шага влевои вправо, для последнего на половину шага вправо и влево от 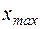 . Пользуясь таким правилом получили бы
. Пользуясь таким правилом получили бы 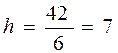 и другой интервальный ряд (таблица 4).
и другой интервальный ряд (таблица 4).
Таблица 4
| Номер i | |||||||
| Границы промежутка | -4.5 2.5 | 2.5 9.5 | 9.5 16.5 | 16.5 23.5 | 23.5 30.5 | 30.5 37.5 | 37.5 44.5 |
| Середина xio | |||||||
| Частота ni |
3 способ Система MathCAD 2000 Pro имеет процедуру составления гистограммы. Для этого вводится одномерный массив Х выборочных данных и при его разбиении на 7 равных промежутков находится двумерный массив 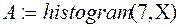 . Программа к максимальному значению х =41 прибавила 1 и нашла шаг разбиения
. Программа к максимальному значению х =41 прибавила 1 и нашла шаг разбиения 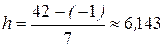 . При этом получили первую составляющую массива А- границы промежутков: -1, 5.14, 11.28, 17.42, 23.57, 29.71, 35.85, 42.00. Второй составляющей массива являются частоты 2, 6, 3, 8, 5, 4, 2 наблюдений элементов в каждом из таких промежутков. В результате получилось другое распределение (таблица 5) с новой гистограммой частот (рисунок 2).
. При этом получили первую составляющую массива А- границы промежутков: -1, 5.14, 11.28, 17.42, 23.57, 29.71, 35.85, 42.00. Второй составляющей массива являются частоты 2, 6, 3, 8, 5, 4, 2 наблюдений элементов в каждом из таких промежутков. В результате получилось другое распределение (таблица 5) с новой гистограммой частот (рисунок 2).
Таблица 5
| Номер i | |||||||
| Границы промежутка | -1 5,14 | 5.14 11.28 | 11.28 17.42 | 17.42 23.57 | 23.57 29.71 | 29.71 35.85 | 35.85 |
| Середина xio | 2,071 | 8,214 | 14,357 | 20,5 | 26,643 | 32,786 | 38,929 |
| Частота ni |
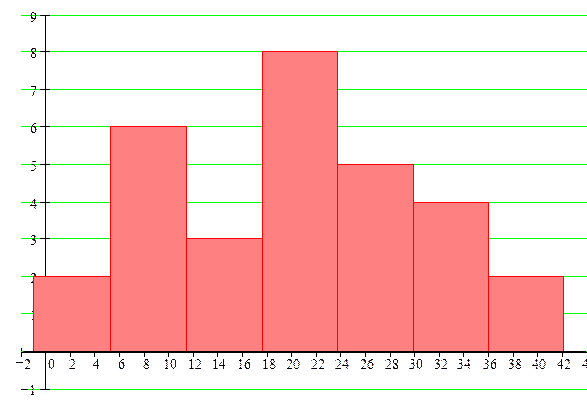

При необходимости разбиения на неравные промежутки в системе MathCAD 2000 Pro применяют другую процедуру-функцию hist, которая массив Х разбивает на промежутки с указанными в дополнительном массиве к +1 границами промежутков. Результатом её применения является одномерный массив частот наблюдений элементов выборки в каждом из указанных промежутков. При этом попадающий на границу двух промежутков элемент учитывается только в правом промежутке, совпадающий с правой границей последнего промежутка элемент выборки не учитывается.
Все дальнейшие действия будем выполнять с первым из полученных статистических рядов (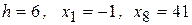 ), записанным в таблице 2.
), записанным в таблице 2.
2 Эмпирическая плотность распределения 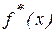 и эмпирическая функция распределения
и эмпирическая функция распределения 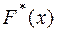
2.1) Вычислим значения эмпирической плотности 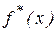 на каждом промежутке по правилу
на каждом промежутке по правилу 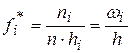 (
(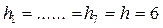 т.к. шаг равный),
т.к. шаг равный),
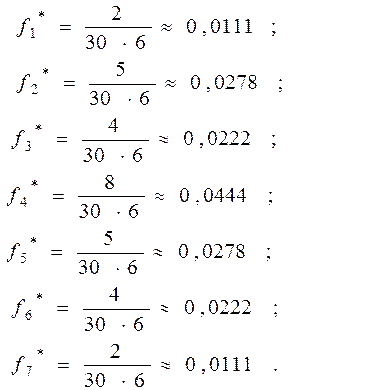
Графиком эмпирической плотности распределения 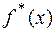 является ступенчатая линия, проходящая по верхним сторонам прямоугольников (аналог гистограммы) см. рисунок 3. При разбиении на равные промежутки такой график получается из гистограммы частот делением высот прямоугольников на постоянное число
является ступенчатая линия, проходящая по верхним сторонам прямоугольников (аналог гистограммы) см. рисунок 3. При разбиении на равные промежутки такой график получается из гистограммы частот делением высот прямоугольников на постоянное число 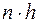 т.е. изменением масштаба по оси ординат.
т.е. изменением масштаба по оси ординат.
График эмпирической плотности распределения

Для большей наглядности вместо ступенчатой линии иногда рассматривается ломаная, соединяющая попарно соседние точки 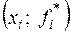 (аналог полигона для дискретного распределения).
(аналог полигона для дискретного распределения).
2.3) Эмпирическая функция распределения
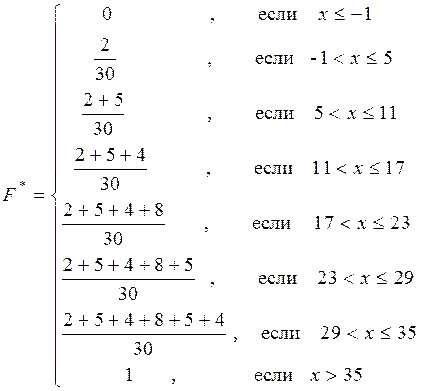
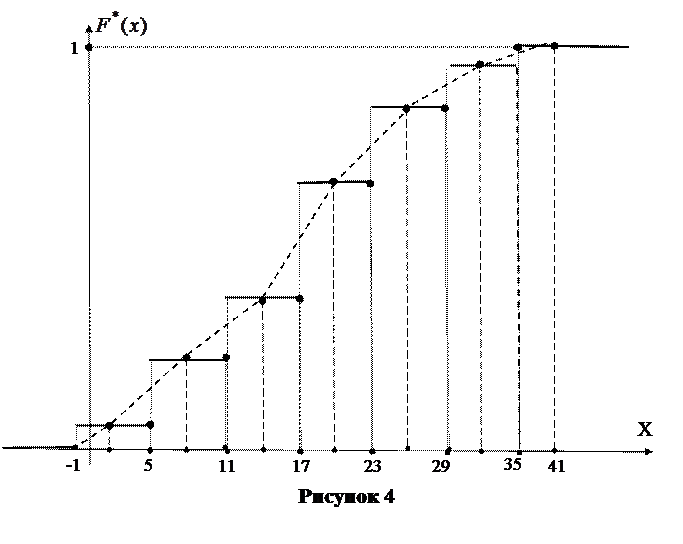 График эмпирической функции распределения
График эмпирической функции распределения
3) Числовые характеристики выборки (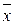 , Dв, S):
, Dв, S):
1 способ вычисления:
а) Выборочное среднее 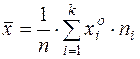 ,
,
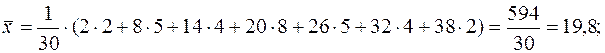
б) Выборочная дисперсия по определению 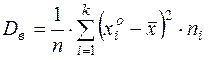
либо по свойству 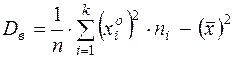 .
.
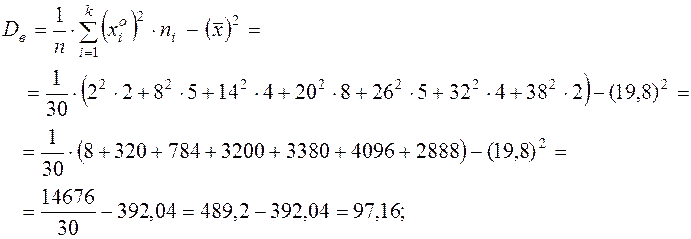 в) При малом объёма выборки (
в) При малом объёма выборки (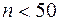 ) выполняют исправление дисперсии по правилу
) выполняют исправление дисперсии по правилу 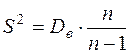 .
.
Исправленная дисперсия 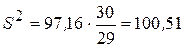 ;
;
г)Исправленное среднее квадратичное отклонение
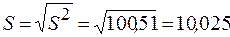 .
.
2 способ вычисления:
Можно ввести «ложный ноль », например варианту с =20 с наибольшей частотой, и вспомогательную величину 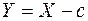 , имеющую распределение
, имеющую распределение
| x-c | -18 | -12 | -6 | ||||
| ni |
.
Тогда получим
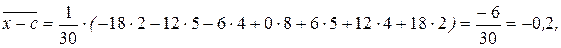
и по свойству средней 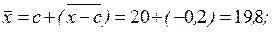
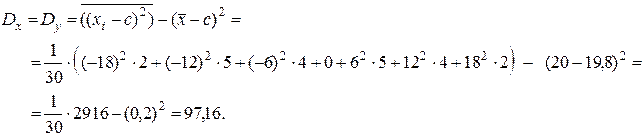 Исправленная дисперсия
Исправленная дисперсия 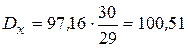 ,
, 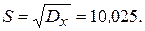
3 способ вычисления:
При вычислении 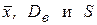 можно было воспользоваться тем, что для вариант распределения выборки выполнено
можно было воспользоваться тем, что для вариант распределения выборки выполнено 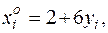 где статистическое распределение Y имеет вид
где статистическое распределение Y имеет вид
| Y | |||||||
| ny |
Тогда по свойствам 
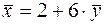 ,
, 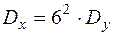 получим
получим
а) 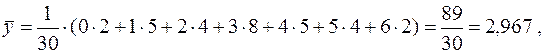
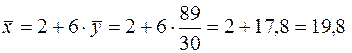 ;
;
б) 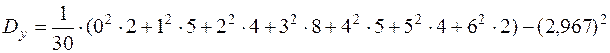 =
=
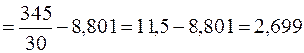 ,
,
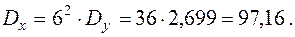
в) 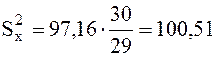 ;
; 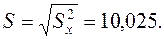
Вывод: Независимо от примененного способа вычислений получили 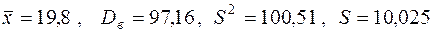 ;
;
4)Предположим, что случайная величина Х, для которой значениями являются элементы выборки, имеет нормальное распределение.
Плотность нормального распределения  ;
;
При 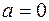 ,
, 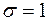 получим нормированное распределение с плотностью
получим нормированное распределение с плотностью 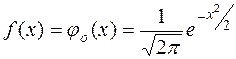 - чётной функцией, заданной таблично (см. приложение А). Функция распределения
- чётной функцией, заданной таблично (см. приложение А). Функция распределения 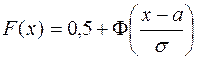 , где
, где 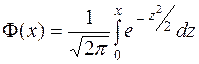 - нечётная функция, заданная таблично (см. приложение Б).
- нечётная функция, заданная таблично (см. приложение Б).
Параметры нормального распределения а и 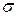 найдём из точечных оценок:
найдём из точечных оценок: 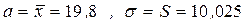 . Тогда плотность распределения
. Тогда плотность распределения
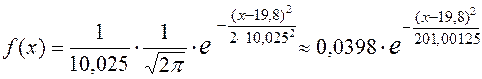 .
.
Для построения графика в серединах промежутков 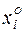 вычислим
вычислим 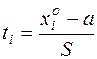 , по таблице приложения А найдём
, по таблице приложения А найдём 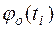 , получая
, получая 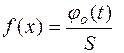 . По точкам
. По точкам 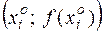 строим непрерывную гладкую линию колоколообразной формы. Желательно его изображать вместе с графиком
строим непрерывную гладкую линию колоколообразной формы. Желательно его изображать вместе с графиком 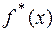 .
.
Все промежуточные результаты удобно представлять в виде сводной таблицы. Для каждого промежутка с номером i (1 £ i £ 7) найдём (см. таблицу 6):
· 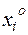 - середина промежутка;
- середина промежутка;
· 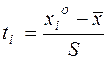 – значения нормированной нормальной случайной величины;
– значения нормированной нормальной случайной величины;
· 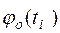 находят по таблице приложения А;
находят по таблице приложения А;
· 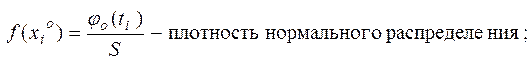
· 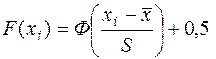 –функция распределения на границах,
–функция распределения на границах,
значения Ф (х) находятся по таблице приложения Б.
Например
Для первого промежутка левой границей считаем 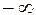 , для которой
, для которой 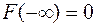 ;
;
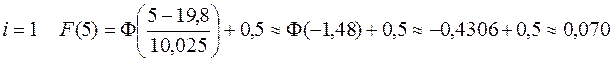
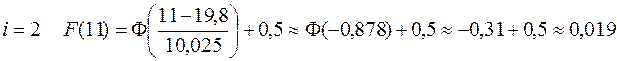 и т.д.; Для последнего промежутка правой границей считаем
и т.д.; Для последнего промежутка правой границей считаем 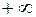 , для которой
, для которой 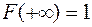 ;
;
· 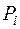 – вероятность попадания в промежуток,
– вероятность попадания в промежуток, 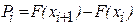 . В силу малых частот на крайних промежутках взяли вероятности
. В силу малых частот на крайних промежутках взяли вероятности
P1+P2 и P6+P7 , объёдинив их с соседними и уменьшив общее
число промежутков;
· 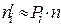 – выравнивающие частоты (округляя до сотых), их сумма должна быть равна исходному объёму выборки.
– выравнивающие частоты (округляя до сотых), их сумма должна быть равна исходному объёму выборки.
Таблица 6
| № | i | 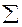
| |||||||
| (xi; xi+1) | -1 – 5 | 5 – 11 | 11– 17 | 17– 23 | 23– 29 | 29– 35 | 35-41 | – | |
| xi0 | – | ||||||||
| ni | |||||||||
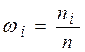
| 0,0667 | 0,1667 | 0,1333 | 0,2667 | 0,1667 | 0,1333 | 0,0667 | 1,000 | |
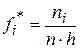
| 0,0111 | 0,0278 | 0,0222 | 0,0444 | 0,0278 | 0,0222 | 0,0111 | – | |
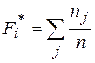
| 0,0667 | 0,2333 | 0,3667 | 0,6333 | 0,8000 | 0,9333 | 1,0000 | – | |
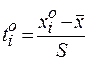
| -1,776 | -1,177 | -0,579 | 0,02 | 0,618 | 1,217 | 1,815 | – | |
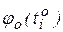
| 0,0825 | 0,2000 | 0,3380 | 0,3989 | 0,3300 | 0,1900 | 0,0770 | – | |
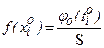
| 0,0082 | 0,0200 | 0,0337 | 0,0398 | 0,0329 | 0,0190 | 0,0077 | – | |
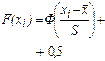
| 0,070 | 0,070 0,190 | 0,190 0,390 | 0,390 0,625 | 0,625 0,820 | 0,820 0,935 | 0,935 | – | |
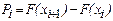
| 0,070 | 0,120 | 0,200 | 0,235 | 0,195 | 0,115 | 0,065 | 1,00 | |
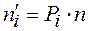
| 2,10 | 3,60 | 6,00 | 7,06 | 5,86 | 3,44 | 1,95 | 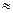 30 30
| |
| 5,7 | 5,39 | ||||||||
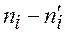
| 1,30 | -2,00 | 0,94 | –0,86 | 0,61 | – | |||
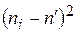
| 1,6900 | 4,0000 | 0,8836 | 0,7396 | 0,3721 | – | |||
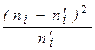
| 0,296 | 0,667 | 0,125 | 0,126 | 0,069 | 1,284 |
Выборочное значение Хи-квадрат 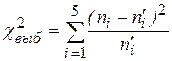 является суммой по последней строке,
является суммой по последней строке, 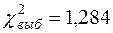 . Число промежутков было уменьшено до k =7–2=5 из-за объединения крайних промежутков с соседними (т.к. частоты n 1=2, n 7=2малы).
. Число промежутков было уменьшено до k =7–2=5 из-за объединения крайних промежутков с соседними (т.к. частоты n 1=2, n 7=2малы).
По таблице критических точек распределения 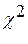 (приложение Д) при числе степеней свободы r = 5–3=2 и уровне значимости
(приложение Д) при числе степеней свободы r = 5–3=2 и уровне значимости 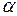 =0,05 найдем
=0,05 найдем 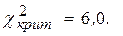 В данном случае
В данном случае 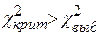 , нет оснований отвергать гипотезу о нормальном распределении.
, нет оснований отвергать гипотезу о нормальном распределении.
Выравнивающие частоты при нормальном распределении изображены на рисунке 5 вместе с выборочными частотами и выравнивающими частотами при равномерном распределении.
Нормальное распределение хорошо согласуется с выборочными данными, найдём доверительные интервалы для параметров нормального распределения при уровне достоверности g=95%:
а) Доверительный интервал для математического ожидания найдём по правилу 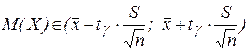 . Объём выборки n =30 можно считать малым (n <50). Значение
. Объём выборки n =30 можно считать малым (n <50). Значение 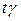 найдём из таблицы приложения В при n =30 и
найдём из таблицы приложения В при n =30 и 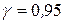 , получим
, получим 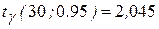 .
.
Подставив n =30, S= 10,025, 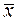 =19,8 получим радиус интервала
=19,8 получим радиус интервала 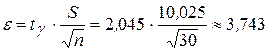 ,
, 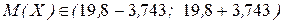 ;
;
б)Доверительный интервал для среднеквадратичного отклонения 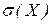 найдём по правилу
найдём по правилу 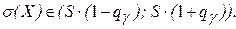
Значение 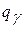 найдём по таблице приложения Г. При n =30 и
найдём по таблице приложения Г. При n =30 и 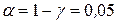 получим
получим 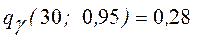 .
.
В таком случае 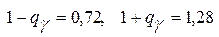 ,
, 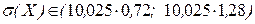 .
.
С вероятность не менее g=95% можно утверждать, что 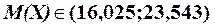 и
и 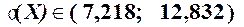 .
.
Числовые характеристики 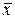 и S для репрезентативных выборок (достаточно большого объёма), элементы которых – значения той же случайной величины Х, будут принимать случайные и каждый раз различные значения. Найденные доверительные интервалы говорят о том, что с вероятностью 95% (допуская в среднем 5 ошибок из ста случаев) можно предполагать. что
и S для репрезентативных выборок (достаточно большого объёма), элементы которых – значения той же случайной величины Х, будут принимать случайные и каждый раз различные значения. Найденные доверительные интервалы говорят о том, что с вероятностью 95% (допуская в среднем 5 ошибок из ста случаев) можно предполагать. что
· выборочное среднее 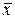 примет значение от 16 до 23,5;
примет значение от 16 до 23,5;
· исправленное выборочное среднее квадратичное отклонение S примет значение от 7,2 до 12,8.
Обработка данных, полученных при других способах составления статистического ряда в п.1, дает иные значения выборочного среднего и среднего квадратичного. Каждый из результатов незначительно отличается от найденного рассмотренным способом и принадлежит найденному доверительному интервалу.
5)Предположим равномерное распределение для Х.
Плотность равномерного распределения 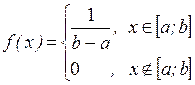 .
.
Параметры а и b найдутся из условия 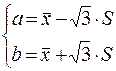 .
.
При S =10,025, 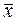 =19,8 получим а =2,436, b =37,163.
=19,8 получим а =2,436, b =37,163.
На отрезке [ a; b ] плотность равномерного распределения 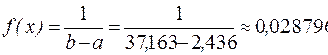 и за пределами отрезка [ a; b ] она равна нулю.
и за пределами отрезка [ a; b ] она равна нулю.
Дальнейшие вычисления выравнивающих частот 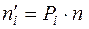 и значения
и значения 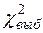 представим в сводной таблице 7. В ней
представим в сводной таблице 7. В ней 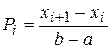 – вероятность попадания в каждый промежуток. Если бы исследуемая случайная величина Х имела равномерное распределение, то её значения лежали бы в отрезке
– вероятность попадания в каждый промежуток. Если бы исследуемая случайная величина Х имела равномерное распределение, то её значения лежали бы в отрезке 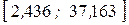 и при этом вероятности попадания в отрезки [-1; a ] и [ b; 41] были бы равны нулю. Поэтому первый и последний промежутки разбиты в таблице 7 на две части.
и при этом вероятности попадания в отрезки [-1; a ] и [ b; 41] были бы равны нулю. Поэтому первый и последний промежутки разбиты в таблице 7 на две части.
В случае, когда хотя бы одна из границ отрезка [ a; b ] выходят за внешние границы (a меньше 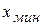 или b больше
или b больше 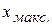 ), то рассматривается дополнительный промежуток с нулевой частотой и ненулевой выравнивающей частотой;– выравнивающая частота каждого промежутка.
), то рассматривается дополнительный промежуток с нулевой частотой и ненулевой выравнивающей частотой;– выравнивающая частота каждого промежутка.
Таблица 7
| № | i | 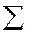
| |||||||||
| ni | |||||||||||
| (xi; xi+1) | -1– a | a – 5 | 5 – 11 | 11– 17 | 17– 23 | 23– 29 | 29– 35 | 35 – b | b – 41 | – | |
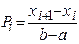
| 0,074 | 0,173 | 0,173 | 0,173 | 0,173 | 0,173 | 0,062 | ||||
| 0,247 | 0,235 | ||||||||||
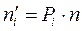
| 7,41 | 5,19 | 5,19 | 5,19 | 7,05 | 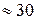
| |||||
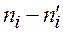
| –0,41 | –1,19 | 2,81 | –0,19 | –1,05 | – | |||||
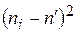
| 0,168 | 1,416 | 7,896 | 0,036 | 1,103 | – | |||||
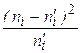
| 0,023 | 0,273 | 1,521 | 0,007 | 0,156 | 1,980 |
В результате вычислений получили 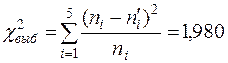 (последняя строка таблицы 7).
(последняя строка таблицы 7).
По таблице критических точек распределения Хи-квадрат (приложение Д) находим 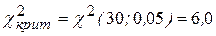 . В данном случае
. В данном случае 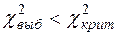 т.е. гипотеза о равномерном распределении также как и о нормальном распределении не отвергается.
т.е. гипотеза о равномерном распределении также как и о нормальном распределении не отвергается.
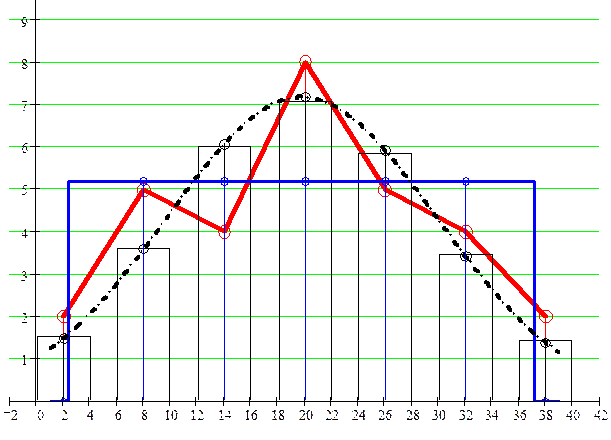
Построим в одной системе координат гистограмму эмпирических частот, гистограммы выравнивающих частот по нормальному распределению и выравнивающих частот по равномерному распределению (Рисунок 5).
На том же рисунке изобразим нормальную кривую, взяв в каждой её точке высотой выравнивающую частоту промежутка, 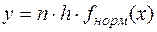 . Полученные точки соединим непрерывной кривой колоколообразной формы, максимальное значение в точке х =19,8 и расстояние от неё до абсцисс точек перегиба составляет 10,025.
. Полученные точки соединим непрерывной кривой колоколообразной формы, максимальное значение в точке х =19,8 и расстояние от неё до абсцисс точек перегиба составляет 10,025.
На том же рисунке изобразим и выравнивающие частоты при равномерном распределении. Каждый из предложенных видов распределения достаточно хорошо согласуется с выборочными данными, значит построенные теоретические линии достаточно хорошо сглаживают ломаную, описывающую изменение эмпирических частот.

6) Прогнозирование
Среди рассмотренных распределений наилучшее согласование с выборочными данными дает нормальноераспределение, т.к. при сравнении выборочных значений Хи–квадрат 1,284 < 1,980.
Тогда вероятность попадания Х в промежуток (10;20) при нормальном распределении случайной величины
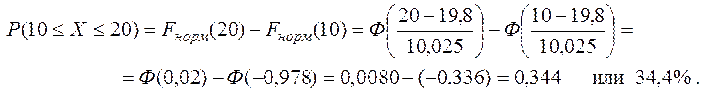
Если бы меньшее значение Хи-квадрат получилось для равномерного распределения, то вероятность попадания Х в промежуток (10;20) была вычислена так:
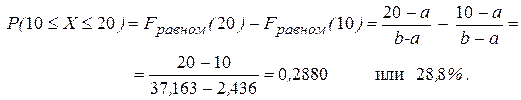
Контрольное задание
В результате пятидесяти измерений случайной величины Х при одинаковых условиях получены данные, записанные в таблице.
На основании выборочных данных требуется:
1) Разбить полученные значения на восемь равных промежутков, составив статистическое распределение выборки;
2) Построить гистограмму частот и график выборочной плотности 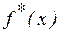 ;
;
3) Найти 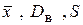 ;
;
4) Предполагая нормальное распределение случайной величины Х,
записать теоретическую плотность распределения f(x),построить её график вместе с 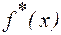 . Оценить согласованность нормального распределения с выборочными данными, используя критерий Пирсона. Найти доверительные интервалы для М(Х) и s(Х);
. Оценить согласованность нормального распределения с выборочными данными, используя критерий Пирсона. Найти доверительные интервалы для М(Х) и s(Х);
5) Предполагая равномерное распределение Х, найти его параметры и плотность распределения f(x), оценить его согласованность с выборочными данными;
6) Среди рассмотренных распределений (нормального и равномерного) выбрать вид, дающий лучшее согласование с выборочными данными, с его помощью найти вероятность попадания Х в промежуток (х1; х2).
(Все вычисления производить с округлением результатов до третьего знака после запятой)
| Вариант№1 | x1=10, x2=25 | Вариант№2 | x1=15, x2=40 |
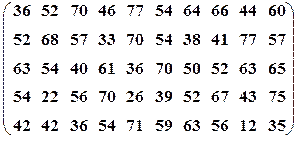
| 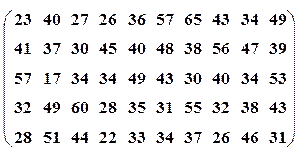
|
| Вариант№3 | x1=15, x2=30 | Вариант№4 | x1=60, x2=75, | ||||
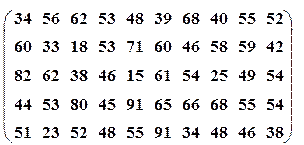
| 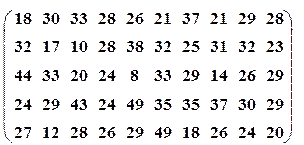
| ||||||
| Вариант№5 | x 1=40, x 2=65 | Вариант№6 | x 1=10, x 2=25 | ||||
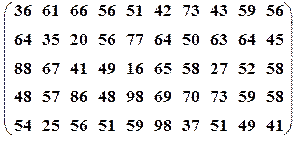
| 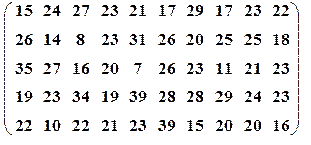
| ||||||
| Вариант№7 | x 1=20, x 2=50 | Вариант№8 | x 1=50, x 2=65 | ||||
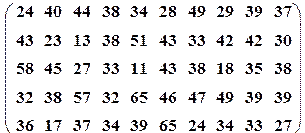
| 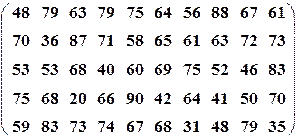
| ||||||
| Вариант№9 | x1=15, x 2=65 | Вариант№10 | x 1=20, x 2=40 | ||||
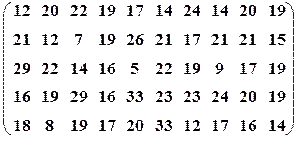
| 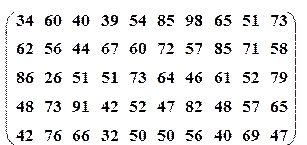
| ||||||
| Вариант№11 | x 1=10, x 2=25 | Вариант№12 | x 1=30, x 2=55 | ||||
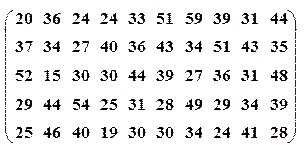
| 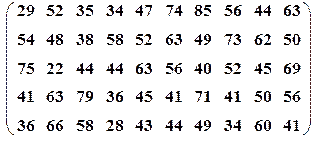
| ||||||
| Вариант№13 | x 1=30, x 2=50 | Вариант№14 | x 1=15, x 2=35 |
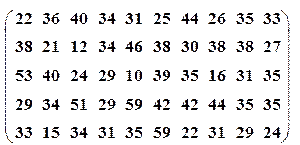
| 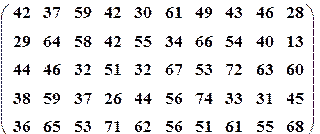
| ||
| Вариант№15 | x 1=30, x 2=80 | Вариант№16 | x 1=20, x 2=55 |
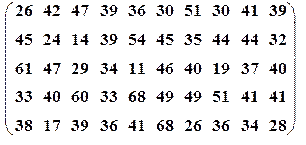
| 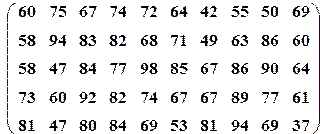
| ||
| Вариант№17 | x 1=30, x 2=55 | Вариант№18 | x 1=20, x 2=60 |
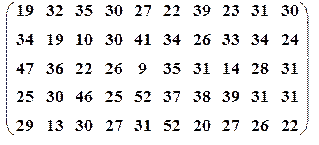
| 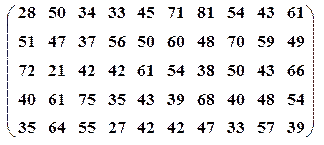
| ||
| Вариант№19 | x 1=30, x 2=55 | Вариант№20 | x 1=30, x 2=45 |
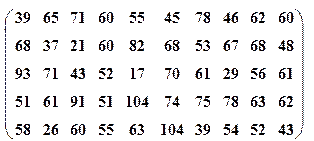
| 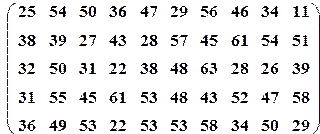
| ||
| Вариант№21 | x 1=30, x 2=55 | Вариант№22 | x 1=30, x 2=70 |
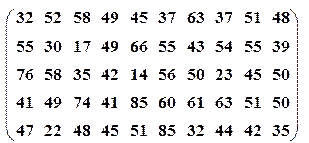
| 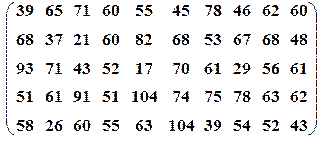
| ||
| Вариант№23 | x 1=20, x 2=60 | Вариант№24 | x 1=30, x 2=55 |
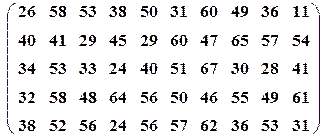
| 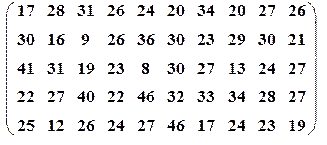
| ||
| Вариант№25 | x 1=30, x 2=70 | Вариант№26 | x 1=10, x 2=60 |
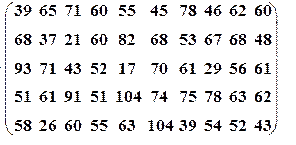
| 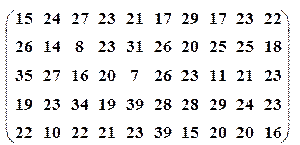
| ||
| Вариант№27 | x 1=30, x 2=55 | Вариант№28 | x 1=30, x 2=55 |
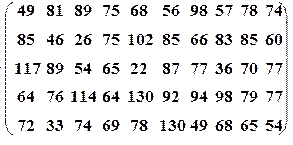
| 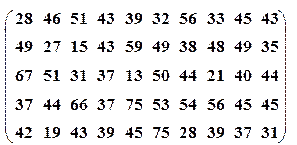
| ||
| Вариант№29 | x 1=20, x 2=80 | Вариант№30 | x 1=30, x 2=55 |
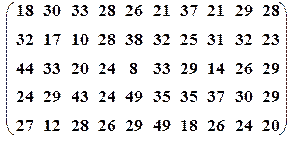
| 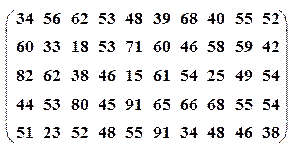
| ||
| Вариант№31 | x 1=0, x 2=50 | Вариант№32 | x 1=30, x 2=55 |
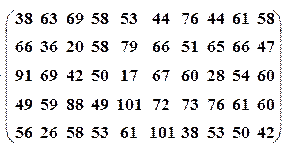
| 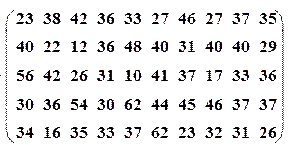
|
Таблица значений функции 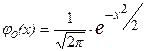
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,0044 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
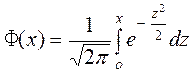
Таблица значений функции
| x | Ф(х) | x | Ф(х) | <
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2020-12-08 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд