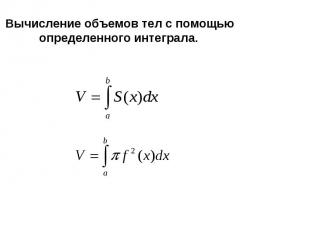Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается  .
.
Выражение  называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
1. 
Производная результата интегрирования равна подынтегральной функции.
2. 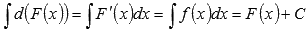
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
3.  , где k – произвольная константа.
, где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.
4. 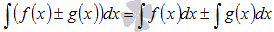
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:
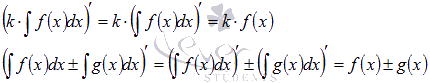
Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Найти первообразную функции 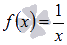 , значение которой равно единице при х = 1.
, значение которой равно единице при х = 1.
Решение.
Мы знаем из дифференциального исчисления, что  (достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом,
(достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом,  . По второму свойству
. По второму свойству 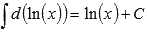 . То есть, имеем множество первообразных
. То есть, имеем множество первообразных 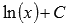 . При х = 1 получим значение
. При х = 1 получим значение 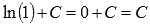 . По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид
. По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид 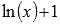 .
.
15. ОСНОВНЫЕ ТАБЛИЧНЫЕ ИНТЕГРАЛЫЭЛЕМЕНТАРНЫХ ФУНКЦИЙ. ПРИМЕРЫ.
1) 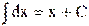 2)
2) 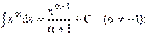
3) 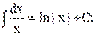 4)
4) 
5) 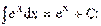 6)
6) 
7) 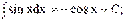 8)
8) 
9)
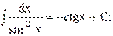 10)
10) 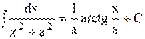
11) 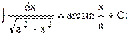 12)
12) 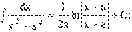
13) 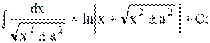 14)
14) 
15) 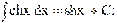 16)
16) 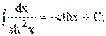
17) 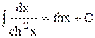 18)
18) 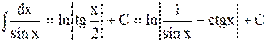
19) 
ПРИМЕР
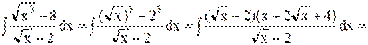

16. МЕТОДЫИНТЕГРИРОВАНИЯ: НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ, МЕТОД ЗАМЕНЫПЕРЕМЕННОЙ И ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ.
Точное нахождение первообразной (или интеграла) произвольных функций — процедура более сложная, чем дифференцирование, то есть нахождениепроизводной. Зачастую выразить интеграл в элементарных функциях невозможно.
Непосредственное интегрирование
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интеграл
Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл  Сделаем подстановку
Сделаем подстановку 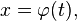 где
где  — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.
Тогда 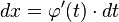 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

Интегрирование по частям
Основная статья: Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
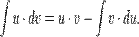
Или:
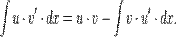
В частности, с помощью n -кратного применения этой формулы находится интеграл
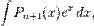
где 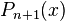 — многочлен
— многочлен 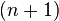 -й степени.
-й степени.
17. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ ДЛЯ НАХОЖДЕНИЯ ПЛОЩАДИ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ. ФОРМУЛА НЬЮТОНА- ЛЕЙБНИЦА
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием интеграла Римана и вычислением первообразной.
Если  непрерывна на отрезке непрерывна на отрезке 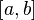 и и  — её любая первообразная на этом отрезке, то имеет место равенство — её любая первообразная на этом отрезке, то имеет место равенство
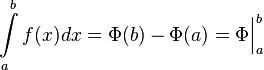
|
18. Решение физических задач с помощью определенного интеграла.