Т(Признак Даламбера)
Пущай для ряда un с положит членами существует предел:
, то
1 Если k<1, то ряд сходится
2 Если k>1 ряд расходится
Т(Признак Коши)
Пусть для того же самого ряда (т. е. положительного) существует предел: 
, тогда
1 Если k<1, то ряд сходится
2 Если k>1 ряд расходится
А вот если эти все пределы по Коши и дедушке Даламберу равны 1, то о сходимости или расходимости ряда ничего сказать нельзя.
Знакочередующиеся ряды. Признак Лейбница.
Ряд называется знакочередующимся если каждая пара соседних членов имеет разные, если считать каждый член сего ряда положительным то его можно записать в виде: 
Т (Признак Лейбница)
Если для знакочередующегося ряды выполняются условия:
1) u1>=u2>=u3…>=un>=un+1…
2) 
то ряд сходится, а его сумма и остаток rn удовлетворяют неравенствам: 0<=S<=un и |rn|<=un+1
Ряд удовлетворяющий условиям теоремы наз. рядом Лейбница.
Если условие чередования знаков выполняется не с первого члена, а с какого-нибудь исчо, то при существовании равного 0 предела ряд будет также сходится.
9 Знакопеременные ряды.
Абсолютная и условная
Сходимость рядов.
Ряд называют знакопеременным, если его членами являются действительные числа, а знаки его членов могут меняться как кому в голову взбредет. Пусть дан ряд:
u1+u2…+un=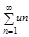 
(1), где un – может быть как положительным, так и отрицательным. Рассмотрим ряд состоящий из абсолютных значений этого ряда:
|u1|+|u2|…+|un|= 
(2),
Если сходится ряд (2), то ряд (1) называют абсолютно сходящимся, а вот если ряд (1) сходится, а ряд (2) расходится. то ряд (1) наз сходящимся условно.
Т. Признак абсолютной сходимости:
Если знакочередующийся ряд сходится условно. то он и просто так сходится, при этом:
|
|
<=
Доквы:
т. к. 0<=|un|+un<=2|un|, то по признаку сравнения сходится ряд |un|+un, тогда сходится ряд: (|un|+un)-|un|=un. Далее, т. к. по св-ву абсолютной величины |Sn|=|u1+u2+…+un|<=|un| " n Î N, то переходя к пределу получим:
<= 
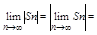
Т2 Если ряд (1) абсолютно сходится, то и любой ряд составленный из тех же членов, но в любом другом порядке тоже абсолютно сходится и его сумма равна сумме ряда un – Sn. А вот с условно сходящимися рядами все гораздо запущенней.
Т(Римана)
Если знакопеременный ряд с действительными членами сходится условно, то каким бы ни было дейст. число S можно так переставить члены ряда, что его сумма станет равна S, т. е. сумма неабсолютно сходящегося ряда зависит от порядка слагаемых
10 Сходимость функциональных последовательностей и рядов
Функциональной последовательностью заданной на множестве Е, наз. последовательность ф-ций {fn(x)} (1)определенных на Е и принимающих числовые действительные значения.
Пусть задана последовательность числовых ф-ций {un(x)} Формально написанную сумму: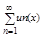 
(2) называют функциональным рядом на множестве Е, а ф-цию un(x) – его членами. Аналогично случаю числовых рядов сумма: Sn(x) = u1(x)+u2(x)+…+un(x) называется частичной суммой ряда n порядка, а ряд: un+1? un+2… - его n-ным остатком. при каждом фиксированном х = х0 Î Е получим из (1) числовую последовательность {fn(x0)}, а из (2) – числовой ряд 
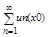, которые могут сходится или расходится. если кто-нибудь из оных сходится, то сходится и функциональная посл (1) в т х0, и сия точка наз. точкой сходимости.
Если посл(1) сход на м-ж Е, то ф-ция f, определенная при " x Î E f(x) =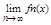 
называется пределом посл (1), если ряд(2) сходится на м-ж Е, то ф-ция S(x) определенная при " x Î Е равенством
|
|
S(x)=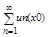
называется суммой ряда (2).
Остаток ряда сходится только когда на этом же м-ж сходится сам ряд., если обозначить сумму остатка ряда через rn(ч), то S(x) = Sn(x)+rn(x)
Если ряд (2) сходится абсолютно, то он наз абсолютно сходящимся на м-ж Е. Множество всех точек сходимости функционального ряда наз областью сходимости. Для определения области сходимости можно использовать признак Даламбера и Коши. С ихнею помашшю ф-ц ряд исследуется на абсолютную сходимость Например, если существует
и
, то ряд (2) абсолютно сходится при k(x)<1 и расходится при k(x)>1.
11 Равномерная
сходимость функциональных