Основные теоретические сведения:
При использовании метода итераций уравнение 
преобразуют к виду 
Предположим, что на интервале 
определен единственный корень этого уравнения ξ.
Алгоритм метода итераций состоит в следующем:
На первом шаге возьмем произвольное значение 
и вычислим 
.
На втором шаге вычислим 
и т.д.
В результате получится рекуррентная последовательность: 
,
n=1,2,3… 
Если эта последовательность сходящаяся, т.е. существует, то переходя к пределу в равенстве , и предполагая функцию 
Или 
т.е. ξ является корнем уравнения.
Геометрически метод итерации иллюстрируется на рис.1 (возрастающая функция) и на рис. 2 (убывающая функция).
Теорема
Пусть функция определена и дифференцируема на отрезке 
, причем все ее значения 
. Тогда, если существует 
такое, что 
, при всех 
, то:
Процесс итерации , N=1,2…, n, … сходится независимо от начального значения 
.
Предельное значение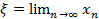 
является единственным корнем уравнения .
Замечание
Скорость стремления 
это скорость геометрической прогрессии. Отделить корни уравнения 
графически и уточнить один из них методом простых итераций с точностью до 0.001.
Решение: Найдем приближенное значение корней графически. Построим графики функций y1=x и y2=cosx.
| X | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| Y1 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| Y2 | 0,877583 | 0,825336 | 0,764842 | 0,696707 | 0,62161 | 0,540302 |
| Y | -0,37758 | -0,22534 | -0,06484 | 0,103293 | 0,27839 | 0,459698 |
Y1=x;
Y2=cos(x).
Из графика видно, что уравнение имеет один корень. Корень уравнения лежит в промежутке [0.5; 1].
Чтобы уточнить корень методом простых итераций, приведем уравнение к виду:
.
Функцию 
будем искать из соотношения:
,
считая, что Ƭ=2/(M+m), где
|
|
m=min|f’(x)|; на промежутке [0,5;1]
M=max|f ’(x)|; на промежутке [0,5;1]
Находим:
f(x)=x-cosx;
f’(x)=1+sinx;
Таблица значений производной f’(x)=1+sinxна промежутке [0,5;1]
| X | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| f '(x) | 1,479426 | 1,564642 | 1,644218 | 1,717356 | 1,783327 | 1,841471 |
На промежутке [0,5; 1] 
возрастает, что видно из таблицы значений производной f ‘(x)=1+sin(x) поэтому
; M=f'(1)=1,841471; m=f’(0,5)=1,4794255; при 
.
Получаем Ƭ=0,60224706, тогда
.
За начальное приближение возьмем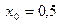 
, все остальные приближения будем определять из равенства
.
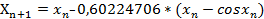Точность вычисления можно оценить из соотношения
,
Где x - точное значение корня а 
Для нахождения значения L находим 
. Значения располагаем в таблице
=1-0,60224706(1+sin(x))
L=0,1090203
Вычисления удобно располагать в таблице:
| 
| 
|
|
| 0,5 | 0,727398 | 0,10902 | |
| 0,727398 | 0,739147 | 0,057699 | |
| 0,739147 | 0,739085 | 0,009775 | |
| 0,739085 | 0,739085 | 0,03427 |
Ответ: x=0,739085;
3. Используя метод Эйлера – Коши, составить таблицу приближенных значений интеграла дифференциального уравнения, удовлетворяющего начальному условию 
на отрезке [0.2; 1.2] с шагом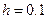 
. Все вычисления вести с четырьмя десятичными знаками.
Основные теоретические сведения:
Заменим интеграл в правой части (3) по формуле левого прямоугольника, получим 
. Отсюда следует основная формула метода Эйлера:
(4)
Метод Эйлера является самым простым методом интегрирования ОДУ, но и не самым грубым.
Если на плоскости переменных 
точки 
, 
соединить ломаной, то получится ломаная Эйлера и она является приближением к интегральной кривой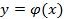 
.
Этот метод естественным образом распространяется на системы ОДУ.
|
|
Сформулируем задачу Коши для системы ОДУ:
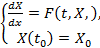(5)
Зафиксируем значения аргумента 
Теперь рекуррентная формула метода Эйлера получает вид:
Решение:
Используем формулу
,
,
.
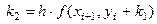Вычисления удобно располагать в таблице:
| 
| 
| 
| 
|
| 
| 
|
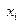
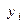
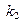
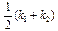
| 0,2 | 0,25 | 0,366727 | 0,036672737 | 0,400920592 | 0,0400921 | 0,0383824 | |
| 0,3 | 0,288382 | 0,40221 | 0,040220968 | 0,441709528 | 0,044171 | 0,04219596 | |
| 0,4 | 0,330578 | 0,443199 | 0,044319867 | 0,488434741 | 0,0488435 | 0,04658167 | |
| 0,5 | 0,37716 | 0,49014 | 0,049014014 | 0,541579615 | 0,054158 | 0,05158599 | |
| 0,6 | 0,428746 | 0,543519 | 0,054351888 | 0,601669405 | 0,0601669 | 0,05725941 | |
| 0,7 | 0,486005 | 0,603862 | 0,060386168 | 0,6692744 | 0,0669274 | 0,0636568 | |
| 0,8 | 0,549662 | 0,67174 | 0,067174046 | 0,745013315 | 0,0745013 | 0,07083769 | |
| 0,9 | 0,6205 | 0,747776 | 0,07477757 | 0,829556929 | 0,0829557 | 0,07886663 | |
| 0,699367 | 0,83264 | 0,083264008 | 0,923631991 | 0,0923632 | 0,0878136 | ||
| 1,1 | 0,78718 | 0,927062 | 0,092706239 | 1,028025413 | 0,1028025 | 0,09775439 | |
| 1,2 | 0,884935 | 1,031832 | 0,103183172 | 0,918040761 | 0,0918041 | 0,09749362 |
Решения дают значения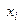 
и 
(
) (первые три столбца таблицы).
Ответ:
|
|
|
|
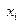
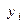
| 0,2 | 0,25 | |
| 0,3 | 0,288382 | |
| 0,4 | 0,330578 | |
| 0,5 | 0,37716 | |
| 0,6 | 0,428746 | |
| 0,7 | 0,486005 | |
| 0,8 | 0,549662 | |
| 0,9 | 0,6205 | |
| 0,699367 | ||
| 1,1 | 0,78718 | |
| 1,2 | 0,884935 |
4. Используя метод Рунге – Кутта, составить таблицу приближенных значений интеграла дифференциального уравнения удовлетворяющего начальному условию 
на отрезке [0;1] с шагом 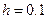. Все вычисления вести с четырьмя десятичными знаками.
Основные теоретические сведения:
Метод Рунге-Кутта 4-го порядка состоит в том, что 
состоит из четырех слагаемых:
,
,
,
,
.
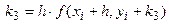Каждое из них находится по своей формуле:
Теперь находим 
Отметим, что метод Рунге-Кутта 4-го порядка является одним из самых распространенных методом интегрирования ОДУ в космонавтике. Его точность вполне удовлетворяет запросы практики.
|
|
Решение:
Значения 
, где 
, 
определятся по формулам
,
,
,
,
,
.
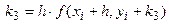Вычисления удобно располагать в таблице:
| 
| 
| 
| 
| 
| 
|
| 0,1 | 0,097881 | 0,097924 | 0,095632 | 0,097874 | ||
| 0,1 | 0,097874 | 0,099122 | 0,096578 | 0,096627 | 0,09397 | 0,096584 |
| 0,2 | 0,194457 | 0,096569 | 0,093715 | 0,093768 | 0,090858 | 0,093732 |
| 0,3 | 0,28819 | 0,092582 | 0,089548 | 0,089599 | 0,086563 | 0,089573 |
| 0,4 | 0,377763 | 0,087524 | 0,084442 | 0,084489 | 0,081452 | 0,084473 |
| 0,5 | 0,462236 | 0,081827 | 0,078824 | 0,078862 | 0,075942 | 0,078857 |
| 0,6 | 0,541093 | 0,075936 | 0,073123 | 0,073151 | 0,070452 | 0,073156 |
| 0,7 | 0,614248 | 0,070265 | 0,067738 | 0,067754 | 0,065367 | 0,067769 |
| 0,8 | 0,682018 | 0,065172 | 0,063013 | 0,063019 | 0,06102 | 0,063043 |
| 0,9 | 0,74506 | 0,060961 | 0,059241 | 0,059239 | 0,057698 | 0,05927 |
| 0,80433 | 0,057892 | 0,05668 | 0,056674 | 0,055661 | 0,05671 |
Окончательные значения 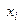и записаны в отдельной таблице:
Ответ:
|
|
|
| 0,1 | 0,097874 |
| 0,2 | 0,194457 |
| 0,3 | 0,28819 |
| 0,4 | 0,377763 |
| 0,5 | 0,462236 |
| 0,6 | 0,541093 |
| 0,7 | 0,614248 |
| 0,8 | 0,682018 |
| 0,9 | 0,74506 |
| 0,80433 |
Заключение
После проделанных вычислений в задании 1 и 2, видим, что заданная точность при нахождении корней нелинейных уравнений была достигнута.
В задании 3 решение дифференциального уравнение было получено методом Эйлера-Коши, составлена сравнительная таблица значений искомой функции.
В задании 4 решение дифференциального уравнение было получено методом Рунге-Кутта, составлена сравнительная таблица значений искомой функции.
Список литературы
1. Вержбицкий В.М. Численные методы. Линейная алгебра и нелинейные уравнения. М.: Оникс 21 век, 2005. – 635 с.
2. Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Оникс 21 век, 2005. – 400 с.
3. Бахвалов Н.С. Численные методы. Н.С. Бахвалов, Н.П. Жидков, Г.М.
Кобельков – М.: Бином. Лаборатория знаний, 2008. – 432 с.