Группа 1-ТПС-5-19
Тема занятия: Понятие многогранника. Призма.
Цели:
Обучающие:
научить выделять многогранники из геометрических тел, а призмы из многогранников;
изучить соответствующую терминологию;
повторить понятие прямоугольного параллелепипеда, его свойств, угла между прямой и плоскостью, перпендикуляр к плоскости в решении задач.
Развивающие:
продолжить формирования умений слушать и анализировать ответы товарищей, математически грамотно формулировать свои ответы и выстраивать логику решения;
научить применять теоретические знания на практике, в решении задач;
продолжить учить работать в группах;
Воспитательные:
воспитывать доброжелательное отношение и терпимость к чужому мнению;
продолжить формирование умений оказывать помощь товарищам и принимать помощь;
учить слушать ответы и правильно оценивать их.
воспитывать аккуратность в работе и доброжелательность.
Теоретический материал для самостоятельного изучения
Многогранники представляют собой простейшие тела в пространстве, подобно тому, как многоугольники – простейшие фигуры на плоскости.
Многогранник можно определить как часть пространства, ограниченную плоскими многоугольниками.
Рассмотрим классификацию многогранников:
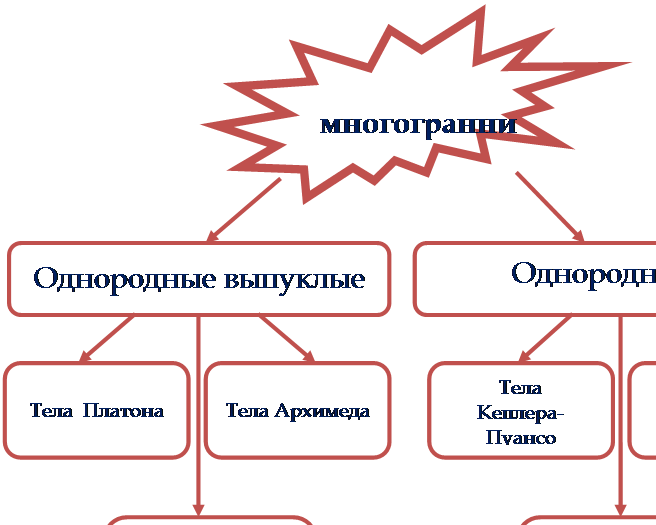
Правильными многогранниками называют выпуклые многогранники, все грани и углы которых равны, причём грани – правильные многоугольники одного типа
другие виды многогранников
 | |||||
 | |||||
 | |||||
 | |||
 | |||
Призма, ее элементы.
Введем понятие призмы, прямой призмы, рассмотрим ее элементы:
|
|
Изображение призмы на плоскости
Рассмотрим построение призмы на плоскости (с помощью анимации на слайдах можно рассмотреть пошаговое построение).
Изображение призмы с данным многоугольником в основании:
- провести из вершин многоугольника параллельные прямые
- отложить на них равные отрезки
- соединить их концы в той же последовательности, как и на заданном основании
Площадь поверхности призмы
Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней
Sполн =Sбок + 2Sосн
Докажем теорему о боковой поверхности прямой призмы.
Теорема: площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту.
Дано: прямая призма h – высота а1,а2,…аn-стороны основания P – периметр основания
Доказать: Sбок = P*h
Доказательство:
Sбок=S1+S2+……+Sn=
=а1*h+а2*h+…..=аn*h = P*h
ЭЙЛЕР Леонард (1707-83), математик, механик, физик и астроном. По происхождению швейцарец. В 1726 был приглашен в Петербургскую АН и переехал в 1727 в Россию. Эйлер — ученый необычайной широты интересов и творческой продуктивности, автор св. 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки, оказавших значительное влияние на развитие науки.
Он ввёл характеристику, которая в последствие стала называться Эйлеровой, а заключается она в нахождение значения следующего выражения В-Р+Г. И оно верно, для произвольного выпуклого многогранника.
|
|
Примеры решения задач:
№ 219. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, АВ = 12 см, ВС = 5 см, угол между АС1 и (ABC) 45°.
Найти: ВВ1.
Решение: Проекцией АС1 на плоскость (ABC) является AC (СС1 ⊥ (ABC), значит, AC ⊥ СС1). Значит, ∠CAC1 = 45°. Имеем: ΔACC1 прямоугольный и равнобедренный АС = СС1 = ВВ1. Найдем АС: Значит, СС1 = ВВ1 = 13 см. (Ответ: 13 см.)
№ 220. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, АВ = ВС, АС = 24 см, BD = 10 cm, AA1 = 10 см.
Найти: большую диагональ.
Решение: Большая диагональ АС1 (так как большая диагональ ромба АС является проекцией диагонали АС1, чем больше ее проекция, тем больше ее наклонная). ΔACC1 - прямоугольный треугольник.
(Ответ: 26 см.)