Задачи оптимизации
По своей сущности задача оптимизации – это математическая модель определенного процесса производства продукции, его распределении, хранении, транспортировки, переработки, покупки или продажи и т.п.
Таким образом, задача оптимизации – это задача выбора из множества вариантов наилучшего, оптимального.
Пример. Задача оптимального использования ресурсов.
Фабрика имеет в своем распоряжении определенное количество ресурсов: рабочую силу, деньги, сырье, оборудование, производственные площади и т.п. Допустим, например, ресурсы трех видов: рабочая сила, сырье и оборудование – имеются в количестве соответственно 80 (чел./дней), 480 (кг) и 130 (станков/ч). Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса, необходимых для производства одного ковра каждого вида, и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в таблице.
| Ресурсы | Нормы расхода ресурсов на единицу изделия | Наличие ресурсов | |||
| Ковер «Лужайка» | Ковер «Силуэт» | Ковер «Детский» | Ковер «Дымка» | ||
| Труд | |||||
| Сырье | |||||
| Оборудование | |||||
| Цена (тыс. руб) |
Требуется найти такой план выпуска продукции, при котором будет максимальной общая стоимость продукции.
Обозначим через Х1, Х2, Х3, Х4 количество ковров каждого типа.
Экономико-математическая модель задачи.
Целевая функция – это выражение, которое необходимо максимизировать:
F(x)=3X1+4X2+3X3+X4.
Ограничения по ресурсам:
7Х1+2Х2+2Х3+6Х4≤ 80
5Х1+8Х2+4Х3+3Х4 ≤ 480
2Х1+4Х2+Х3+8Х4 ≤ 130
Х1, Х2, Х3, Х4 ≥ 0.
Рассмотрим технологию решения задача оптимального использования ресурсов
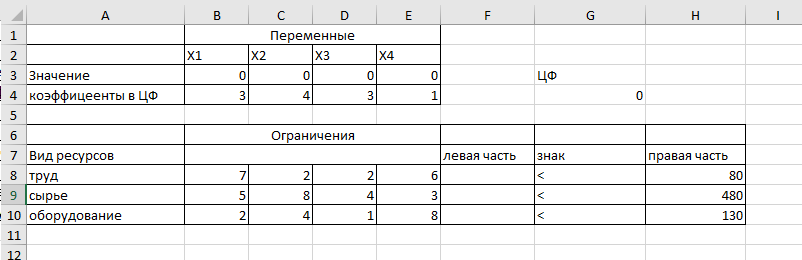
1. Подготовим форму для ввода условий.
2. В нашей задаче оптимальные значения Х1, Х2, Х3, Х4 будут помещены в ячейках В3:Е3, оптимальное значение целевой функции – в ячейке G4.
3. Введем исходные данные в созданную форму. Получим:
(Чтобы объединить ячейки, необходимо выделить те ячейки, которые объединяем и нажать на кнопку  на панели инструментов)
на панели инструментов)
4. Введем зависимость для целевой функции. Для этого поставим курсор в ячейку G4 и введем в нее формулу: =$B$3*B4+$C$3*C4+$D$3*D4+$E$3*E4.
5. В ячейку F8 введите формулу: =B8*$B$3+C8*$C$3+D8*$D$3+E8*$E$3 и скопируйте в остальные две ячейки.
6. Запустим Поиск решения. Поиск решения – это надстройка Excel, которая позволяет решать оптимизационные задачи. Если в меню Данные отсутствует Поиск решения, значит, необходимо загрузить эту надстройку. Для этого выполните команду: Файл – Параметры – Надстройки, в нижней части экрана нажмите на Перейти и в окрывшемся диалоговом окне поставьте галочку рядом с надписью Поиск решения, затем ОК.
7. В диалоговом окне Поиск решения есть три основных параметра: Установить целевую ячейку, Изменяя ячейки и Ограничения. Для того, чтобы установить целевую ячейку, нужно в окне Оптимизировать целевую функцию ввести: $G$4 (как привило она уже там будет стоять, если вы ранее выделили эту ячейку до запуска Поиска решения. Поскольку мы хотим найти наибольшую прибыль, необходимо выбрать Максимум.
8. В поле Изменяя ячейки переменных введем: $B$3:$E$3, для этого просто выделим указанный диапазон ячеек.
9. Остается ввести ограничения. Для этого нажмите кнопку Добавить и в появившемся окне введите:
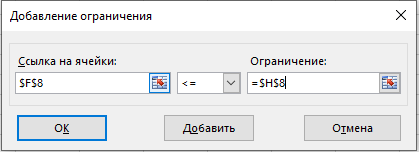
10. Добавьте остальные ограничения таким же образом. В результате должно получиться следующее:
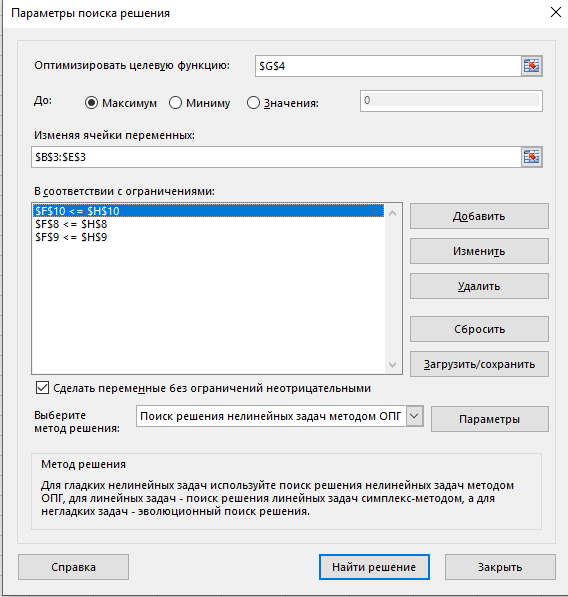
11. Нажмите на Найти решение. Должно получиться:

Полученное решение означает, что максимальный доход 150 тыс. руб. фабрика может получить при выпуске 30 ковров второго вида и 10 ковров третьего вида. При этом ресурсы труд и оборудование будут использованы полностью, а из 480 кг сырья будет использовано 280 кг.