ПРИЛОЖЕНИЕ к статье
Вычисление интеграла, используемого в статье А. Рождественского «Астрономические колебания солнечной радиации как усилитель зонального охлаждения или разогрева климата».
В приложении нумерация формул начинается с начала.
Интеграл (7) можно найти в общем виде, если задающие вынужденные колебания радиации на верхней границе атмосферы принять как гармонические колебания, а вынужденные колебания радиации в приземном слое представить как следствие, т.е колебания ч теми же частотами, но разными амплитудами и фазами. В этом случае постановка задачи о расчете интеграла вида (5) и ее решение в общем виде выглядит следующим образом:
G =  =
= 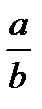 { Cos [ ω(τa –τb)] –
{ Cos [ ω(τa –τb)] –
- 2 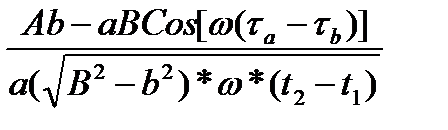 *
*
*(ArcTan[  ] -
] -
- ArcTan[ 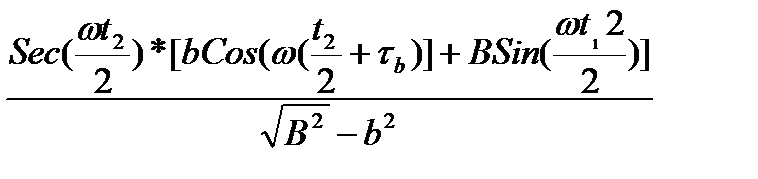 ]*
]*
*  *Log{
*Log{ 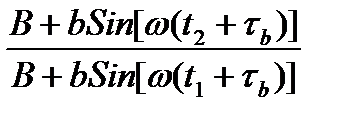 }; (**)
}; (**)
При ( << (
<< ( ), a < A, b < B точный интеграл G (**) с большой точностью сводится к приближенному интегралу (5) в тексте статьи.
), a < A, b < B точный интеграл G (**) с большой точностью сводится к приближенному интегралу (5) в тексте статьи.
Точное значение интеграла вида (7) при гармонических колебаний температур, аналогичного интегралу (**), имеется. Однако это выражение громоздко (занимает объем, почти сравнимый с объемом статьи) и не удобно для изучения.
Поэтому вначале получим упрощенное приближенное значение этого интеграла, а затем вычисли его для гармонических колебаний.
Расчет интеграла вида (7) ( нумерация по основному тексту статьи)
Обозначим функцию (Ф) следующим образом (см. выражение (9) для краткости введем новую нумерацию с начала:
Ф = 
 )* (1 +
)* (1 +  +
+ 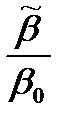 ) =
) =
 {(
{(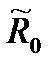 )+
)+  +
+ 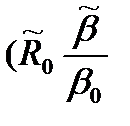 )+
)+  +
+  (
( ) +
) +  (
(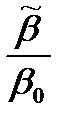 )} (1)
)} (1)
При этом положим как в статье (9) см. выше:
<Т> = A 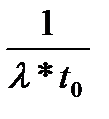
 (2)
(2)
 =
=  {
{  +τ
+τ  +
+  (
( )dt +
)dt +  +τ
+τ  dt +τ
dt +τ  +
+
+ τ 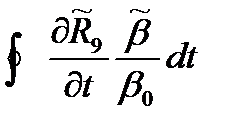 =
= 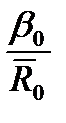 {
{  +
+  +τ
+τ  +τ
+τ 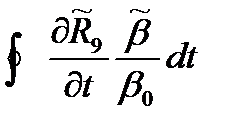 }; (3)
}; (3)
Далее приложение посвящено расчету интеграла аида (3)
Оценку последним четырем интегралам для  в (3) сделаем для гармонических колебаний
в (3) сделаем для гармонических колебаний  = a*sin(ωt);
= a*sin(ωt);
 =b*sin(ω(t+
=b*sin(ω(t+  ) = =b*[ sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτ)].
) = =b*[ sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτ)].
1.  = а*b [cos(ωτ)
= а*b [cos(ωτ)  +sin(ωτ)
+sin(ωτ)  =
=
=a*b*Cos(ωτb)*  (4)
(4)
2. Заметим, что  = xcos(x) +sin(x) + C.
= xcos(x) +sin(x) + C.  +C. Отсюда
+C. Отсюда
 =
= 
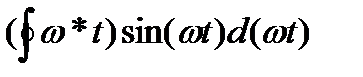 =
= 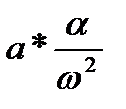 [
[  +sin(ωt)]
+sin(ωt)] 
 -0
-0  =
=
= a*α  (5)
(5)
3.  =
= 
 =
=  [(
[( )
) 
 -0
-0  -
-  ≡ 0 (6)
≡ 0 (6)
4.  =
=  *[ sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt =
*[ sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt =
=sin(ωtb)*  *π*
*π*  (7)
(7)
В итоге получаем с учетом (3-7):
 =
=  {
{  a*b*Cos(ωτb)*
a*b*Cos(ωτb)*  +
+  * a* α
* a* α  + sin(ωtb)*
+ sin(ωtb)*  *π*
*π* 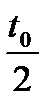 } (8)
} (8)
Далее рассмотрим интеграл  и отдельные интегралы после раскрытия скобок:
и отдельные интегралы после раскрытия скобок:
Ф*  =
= 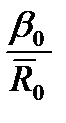 { {(
{ {(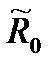
 )+
)+  +
+  )+
)+ 
 +
+  (
( )
) 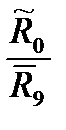 +
+  (
(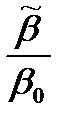 )
)  } (9)
} (9)
1. 
 =
=  (10)
(10)
2.  =
= 
 -0 =
-0 = 
 (11)
(11)
2.  =
=  = a
= a 
 =
=  -
-
- 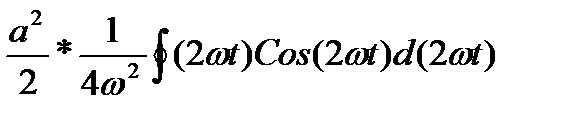 =
=  +
+  {2ωt*sin(2ωt) +cos(2ωt)}
{2ωt*sin(2ωt) +cos(2ωt)}  -0 =
-0 =
= 
 ; (12)
; (12)
3.  =
=  b*a
b*a  (sin(ωt))
(sin(ωt))  * [sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt =
* [sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt =
b*a 
 (
( [sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt (13)
[sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt (13)
Причято во внимание, что:
Cos(2ωt)cos(ωt) =  { cos(ωt)+ cos(3ωt) }
{ cos(ωt)+ cos(3ωt) }
Cos(2ωt)Sin(ωt)=  { sin(3ωt) –sin(ωt) }
{ sin(3ωt) –sin(ωt) }
 ≡ 0; (14)
≡ 0; (14)
4.  (
(
 )dt =
)dt = 
 -0 =
-0 =  ; (15)
; (15)
5. 
 (
( )
) 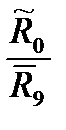 dt =
dt = 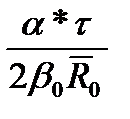

 =
= 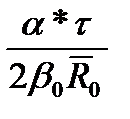 {
{ 
 -0 -
-0 -  (
( )dt}
)dt}
 =
=  *t
*t  -0 =
-0 =  -
-  =0
=0

 (
( )
) 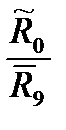 dt ≡ 0; ( 16 )
dt ≡ 0; ( 16 )
6. 
 (
(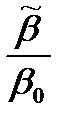 )
) 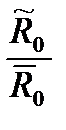 dt =
dt =
= 
 {ωCos(ωt)*Sin(ωt)*[ [sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt
{ωCos(ωt)*Sin(ωt)*[ [sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt
 Sin (ω)
Sin (ω)  Cos(ωt),=
Cos(ωt),= 


 (Sin(3ωt) +sin(ωt)) ≡ o
(Sin(3ωt) +sin(ωt)) ≡ o
Cos(ωt)  sin(ωt) =sin(ωt) –Sin(ωt)
sin(ωt) =sin(ωt) –Sin(ωt)  = sin(ωt) –{
= sin(ωt) –{ 
 {ωCos(ωt)*Sin(ωt)*[ [sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt ≡ 0
{ωCos(ωt)*Sin(ωt)*[ [sin(ωt)*cos(ωτ) +cos(ωt)*sin(ωτb)]dt ≡ 0

 (
(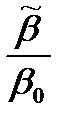 )
) 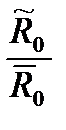 dt = 0; (17)
dt = 0; (17)
Собираем сумму интегралов. (9-17):
 Фdt =
Фdt =  =
=  { a*b*Cos(ωτb)*
{ a*b*Cos(ωτb)*  +a* α
+a* α  +
+  sin(ωtb)*
sin(ωtb)*  *π}
*π}
 Ф*
Ф*  dt =
dt =  {
{  +
+ 
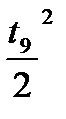 +
+  } (18)
} (18)
<Т> = A 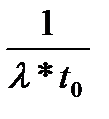
 = A
= A 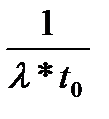 (1 +
(1 +  -
- 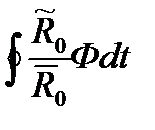 ) (19)
) (19)
Δ =  -
-  =
=  {(β
{(β  abCos Cos(ωτb)*
abCos Cos(ωτb)*  -
-  )+ (a* α
)+ (a* α  -
-
- 
 )+ (sin(ωtb)
)+ (sin(ωtb)  *π*
*π*  -
-  ) }; (20)
) }; (20)
Положим τb <<π, b ≈a/2, климатический квазилинейные тренд повышения температур (антропогенный) α << 1. В этом случае почленное сравнение величин в скобках дает знак величины (Δ)
(a*b*Cos(ωτb)*  -
-  ) ≈ (β
) ≈ (β 
 -
-  ) =
) =  -
-  ) (21)
) (21)
(a* α 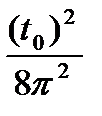 - α*
- α* 
 ) =
) =  (
( -
-  ) (22)
) (22)
(sin(ωtb)  τ*π*
τ*π*  -
-  ) =
) = 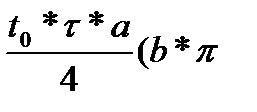 -
-  ) (23)
) (23)
Отметим, что выражениях (1-3) в скобках стоят безразмерные величины, где (а) –амплитуда сезонных колебаний радиации (неравномерная по земному шару). Величина (а) есть амплитуда колебаний радиации (сезонной), по размерности одинакова с постоянной радиацией  . Отношение
. Отношение  равно нулю в обширных экваториальных площадях Земли, и достигает максимума в средних широтах северного полушария
равно нулю в обширных экваториальных площадях Земли, и достигает максимума в средних широтах северного полушария  ≈0,5. Безразмерный интегральный коэффициент доли поглощения длинноволновой радиации в атмосфере (поглощательная способность принимается равной излучательной способности) принят в размере
≈0,5. Безразмерный интегральный коэффициент доли поглощения длинноволновой радиации в атмосфере (поглощательная способность принимается равной излучательной способности) принят в размере  ≈ 0,5, коэффициент безразмерной сезонной амплитуды этого коэффициента b ≈ 0,3.
≈ 0,5, коэффициент безразмерной сезонной амплитуды этого коэффициента b ≈ 0,3.
Таким образом, величина (Δ) в (20) равна:
(Δ) =  {
{  -
-  ) +
) +  (
( -
-  ) +
) + 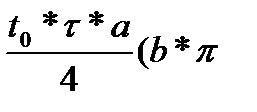 -
-  )}
)}
Отсюда:
<Т> = A 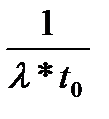
 = A
= A 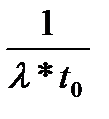
 = A/λ(1 –Δ/
= A/λ(1 –Δ/  ) =
) =
= A/λ{1 + 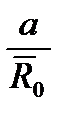 {
{  -
-  ) +
) +  (
( -
-  ) +
) +  -
-  ) } (24)
) } (24)
Выражение (24) далее анализируется и обсуждается в основном тексте статьи и помещено там помещено под номером (10).