Часть 3. Интегральное исчисление для функций одной переменной
Глава 10. Неопределенный интеграл
Первообразная функция и неопределенный интеграл
Часто встречаются задачи, в которых требуется находить функции по их производным. Например, известен угловой коэффициент касательной, проведенной в точке x, k = f(x). Нужно определить уравнение кривой, т.е. такую функцию
y = F(x), что F′(x) = f(x). Или по ускорению a(t) определить скорость v(t) и путь s(t).
Пусть функция f(x) определена на конечном или бесконечном промежутке P.
Определение 1. Функция F(x), определенная на P, называется первообразной или примитивной для функции f(x), если F′(x) = f(x), x ϵ P.
Всякая функция f(x) имеет бесконечное множество первообразных. Например, f(x) = 2x имеет первообразные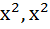 
+1, … Если F(x) – первообразная для f(x), то F(x)+C, C=const, тоже является первообразной для f(x), т.к. (F(x)+C)′ = F′(x) = f(x).
Если 
и 
– две первообразные для f(x), то 
C (параграф 78). Таким образом, если F(x) – первообразная для f(x), то F(x)+C, C=const, - множество всех первообразных для f(x).
Определение 2. Совокупность всех первообразных для функции f(x), определенных на промежутке P, называется неопределенным интегралом функции f(x) на множестве Р и обозначается через 
.
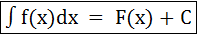; х – переменная интегрирования; f(x) – подынтегральная функция; f(x)dx – подынтегральное выражение; ∫ - знак интеграла; F(x) – любая из первообразных для f(x); С – постоянная интегрирования. Операция нахождения неопределенного интеграла называется интегрированием.
Свойства неопределенного интеграла
Условимся, что все рассматриваемые здесь функции определены на одном и том же промежутке.
1. ()′ = (F(x)+C)′ = f(x) по определению неопределенного интеграла.
2. d() = ()′ dx = f(x)dx
3. f(x)dx = F′(x)dx = dF(x), т.е. = 
= F(x)+C.
4. 
= 
. Производные обеих частей равны 
5. 
. Так же.
Пример 1.
Иногда из множества всех первообразных нужно выделить ту, которая при заданном 
принимает значение 
. Для этого следует найти соответствующую постоянную С.
Пример 2. Найти ту первообразную для 
, которая при 
равна 3.
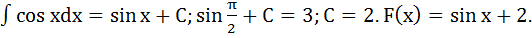
Табличные интегралы
Так как интегрирование – обратная операция относительно дифференцирования, то каждая формула дифференцирования, может быть записана в виде интеграла. Например, т.к. 
, то 
Отдельно рассмотрим функцию y = f(x) = 
. 
. Значит
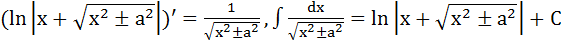
Таблица основных интегралов.
1) 
2) 
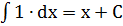
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
11) 
12) 
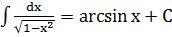
13) 
14) 
15) 
16) 
17) 
Для проверки любой из этих формул достаточно убедиться, что производная правой части равна подынтегральной функции.
Интегрирование подстановкой
(замена переменной)
Пусть функция f(x) на промежутке Р имеет первообразную F(x),т.е.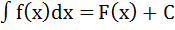 
. Положим 
, функция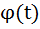 
дифференцируема и имеет на P однозначную обратную функцию 
. Рассмотрим функцию F(
.
Значит, функция 
имеет первообразную 
, т.е.
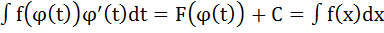. Так как
то
(1)
Формула (1) – формула интегрирования подстановкой, т.е. заменой переменной. Ее используют обычно двояко.
1) Часто трудно вычислить непосредственно. Удачно подобрав подстановку 
, можем получить интеграл, который вычисляется легче. Затем нужно обратно заменить t через x.
Пример 1.
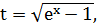т.е.
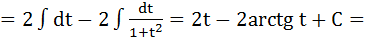
Пример 2.
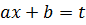
2)Иногда подынтегральное выражение f(x)dx можно представить в виде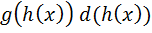 
. Полагая t = h(x), получим
Пример 3.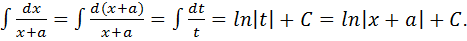 
Пример 4. 
Интегрирование по частям.
Пусть u(x) и v(x) – дифференцируемые функции от х, 
существует. Т.к. (uv)′ = u′v + uv′, т.е. uv′ = (uv)′ - u′v, то
, т.е. 
Отнеся постоянную C к интегралу , имеем
(1)
– формула интегрирования по частям.
Так как существует по условию, то 
тоже существует. Метод используется следующем образом. В 
выделяем 
и 
, затем находим 
, а из 
интегрированием находим v и используем формулу (1). Нужно и выбрать так чтобы:
1. из легко находилась 
;
2. вычислялся легче, чем .
Иногда интегрирование по частям приходится применять несколько раз.
Пример 1.
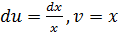
Пример 2.
