Не всякая элементарная функция имеет в качестве своей первообразной тоже элементарную функцию. Можно указать множество интегралов от элементарных функций, которые не выражаются через элементарные функции:
 и т.д.
и т.д.
Если интеграл не выражается через элементарные функции, то говорят, что он не берется в конечном виде. Такие интегралы представляют собой некоторые неэлементарные функции (высшие трансцендентные функции).
Глава 11. Определенный интеграл.
85. Задачи, приводящие к понятию
определенного интеграла
I. Задача о площади.
Пусть функция f(x) непрерывна и положительна на  . Вычислим площадь фигуры, ограниченной кривой y = f(x) и прямыми
. Вычислим площадь фигуры, ограниченной кривой y = f(x) и прямыми
x = a, x = b, y = 0. Эта фигура называется криволинейной трапецией. Разобьем  на n произвольных частей точками
на n произвольных частей точками  , проведем в них ординаты. Сегмент
, проведем в них ординаты. Сегмент  разобьется на n частичных сегментов
разобьется на n частичных сегментов  . Их длины обозначим через
. Их длины обозначим через  соответственно.
соответственно.
Криволинейная трапеция разбилась на n полос. Площадь каждой полосы приближенно заменим площадью прямоугольника с основанием  и высотой, равной любой из ординат на этом частичном сегменте, например в точкe
и высотой, равной любой из ординат на этом частичном сегменте, например в точкe  . Площадь i-ой полоски приближенно равна
. Площадь i-ой полоски приближенно равна  , а площадь всей криволинейной трапеции
, а площадь всей криволинейной трапеции  . Если число точек деления безгранично увеличивать так, чтобы
. Если число точек деления безгранично увеличивать так, чтобы  , то ступенчатый многоугольник будет иметь площадь, все более приближающуюся к площади P криволинейной трапеции. Пришли к вычислению предела суммы
, то ступенчатый многоугольник будет иметь площадь, все более приближающуюся к площади P криволинейной трапеции. Пришли к вычислению предела суммы
 .
.
II. Задача о работе. Пусть материальная точка движется прямолинейно под действием силы F. Вычислим работу, совершаемую силой при перемещении точки из M в N. Пусть a и b - абсциссы этих точек. Если сила F постоянна, то работа
A = F(b – a).
Пусть 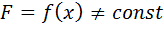 . Разобьем MN на n произвольных частей точками
. Разобьем MN на n произвольных частей точками 
 . Силу F на каждом частичном сегменте
. Силу F на каждом частичном сегменте  заменим постоянной силой Q, равной значению F в какой-нибудь точке
заменим постоянной силой Q, равной значению F в какой-нибудь точке
 . Работа силы Q на
. Работа силы Q на  равна
равна
 . Работа силы F на MN приближенно равна
. Работа силы F на MN приближенно равна
 .
.
Если при безграничном увеличении числа точек деления и  эта сумма имеет предел, то его и примем за работу A.
эта сумма имеет предел, то его и примем за работу A.
86. Интегрируемость функции
и определенный интеграл
Пусть на  задана функция
задана функция  . Разобьем
. Разобьем  на n произвольных частей точками деления
на n произвольных частей точками деления  . Эту систему точек
. Эту систему точек
 назовем разбиением T сегмента
назовем разбиением T сегмента  .
. 

Число  зависит от разбиения T, т.е.
зависит от разбиения T, т.е.  . Выберем произвольную точку
. Выберем произвольную точку  и составим сумму
и составим сумму

Определение 1. Сумма (1) называется интегральной суммой или суммой Римана для функции  на
на 
Значение суммы  зависит от разбиения Т и от выбора точек
зависит от разбиения Т и от выбора точек 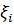 . Геометрически каждое слагаемое
. Геометрически каждое слагаемое  – площадь прямоугольника с основанием
– площадь прямоугольника с основанием  и высотой
и высотой  . Эти прямоугольники составляют ступенчатый многоугольник, площадь которого равна
. Эти прямоугольники составляют ступенчатый многоугольник, площадь которого равна  .
.
Определение 2. Число  называется пределом интегральных сумм
называется пределом интегральных сумм  , если
, если  такое, что для любого разбиения T сегмента
такое, что для любого разбиения T сегмента  , удовлетворяющего условию
, удовлетворяющего условию  , и для любого выбора точек
, и для любого выбора точек  выполняется неравенство
выполняется неравенство  . Пишут
. Пишут

Это определение предела является новым понятием, не укладывающимся в рамки уже известных нам определений пределов.
Определение 3. Если существует  , то этот предел называется определенным интегралом функции
, то этот предел называется определенным интегралом функции  на
на  .
.
Пишут  , a - нижний, b - верхний предел интегрирования.
, a - нижний, b - верхний предел интегрирования.
Определение 4. Функция  , для которой существует
, для которой существует  , называется интегрируемой на
, называется интегрируемой на 
Теорема 1. Функция, интегрируемая на  , ограничена на
, ограничена на 
Доказательство. Допустим противное, т.е. пусть  не ограничена на
не ограничена на  . T – произвольное разбиение
. T – произвольное разбиение  . Так как
. Так как  не ограничена на
не ограничена на  , то она не ограничена по крайней мере на одном
, то она не ограничена по крайней мере на одном 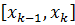 . Выбрав точку
. Выбрав точку
 подходящим образом, слагаемое
подходящим образом, слагаемое  можно сделать как угодно большим по абсолютной величине. Но тогда суммы
можно сделать как угодно большим по абсолютной величине. Но тогда суммы  при
при  не могут иметь конечного предела. Теорема доказана.
не могут иметь конечного предела. Теорема доказана.
87. Нижние и верхние интегральные суммы
Пусть  определена на
определена на  , Т – разбиение
, Т – разбиение  ,
, 
 ,
,  Составим суммы
Составим суммы

Если интегрируема на  , то она ограничена на
, то она ограничена на  .
.
Поэтому суммы s и S имеют смысл и зависит только от разбиения Т. Пишут s(T), S(T). Сумма S(T) называется верхней интегральной суммой Дарбу, s(T) - нижней интегральной суммой Дарбу.
1) Так как при  любом выборе точек
любом выборе точек
 , то
, то 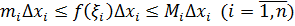 . Отсюда
. Отсюда
 , т.е.
, т.е.  .
.
Таким образом, сумма, соответствующая данному разбиению Т, лежит между, соответствующими тому же разбиению Т.
2) Так как  , то
, то  –
–  по определению верхней грани не является таковой на
по определению верхней грани не является таковой на  . Поэтому существует
. Поэтому существует  , в которой
, в которой  . Тогда
. Тогда 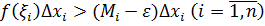 и
и
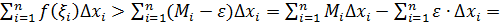
 , т.е.
, т.е.  . Так как
. Так как  как угодно мало, то существуют интегральные суммы
как угодно мало, то существуют интегральные суммы  как угодно мало отличающиеся от
как угодно мало отличающиеся от  . С другой стороны,
. С другой стороны,  . Таким образом,
. Таким образом,  - верхняя грань для интегральных сумм
- верхняя грань для интегральных сумм  , соответствующих данному разбиению
, соответствующих данному разбиению  .
.
 . Аналогично
. Аналогично  .
.
Когда  непрерывна на
непрерывна на  числа
числа  является соответственно наибольшим и наименьшим значениям функции
является соответственно наибольшим и наименьшим значениям функции  на
на 
Значит, для непрерывной функции сумма  – наибольшая из интегральных сумм,
– наибольшая из интегральных сумм,  - наименьшая, соответствующих данному разбиению.
- наименьшая, соответствующих данному разбиению.
88. Свойства сумм Дарбу
Теорема 1. Если к имеющимся точкам деления добавить новые точки, то нижняя сумма Дарбу не уменьшится, верхняя не увеличится.
Доказательство. Для доказательства достаточно ограничиться случаем, когда добавляется одна точка 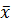 . Пусть
. Пусть 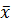 попадает между точками
попадает между точками  и
и  , т.е.
, т.е.  . Пусть
. Пусть  ,
, 
 ,
, 

 .
.
Так как  и
и  – части
– части 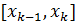 , то
, то  ,
,
 ,
,  . В новой нижней сумме слагаемое
. В новой нижней сумме слагаемое  заменено суммой
заменено суммой  , т.е. нижняя сумма не уменьшится. С верхней – аналогично.
, т.е. нижняя сумма не уменьшится. С верхней – аналогично.
Теорема 2. Всякая нижняя сумма Дарбу не больше любой верхней суммы.
Доказательство. Для одного и того же разбиения теорема очевидна, т.к. из  имеем
имеем  , откуда
, откуда  .
.
Пусть  и
и  – два произвольных разбиения, никак не связанные между собой. Докажем, что
– два произвольных разбиения, никак не связанные между собой. Докажем, что  . Рассмотрим разбиение
. Рассмотрим разбиение  , являющиеся объединением
, являющиеся объединением  и
и  . Разбиение
. Разбиение  можно получить из
можно получить из  , добавлением всех точек из
, добавлением всех точек из  и наоборот. По теореме 1 имеем:
и наоборот. По теореме 1 имеем:


Кроме того, 
Из (1), (2), (3) получаем  . Теорема доказана.
. Теорема доказана.
Таким образом, множество всех нижних сумм ограничено сверху, например любой верхней суммой  . Следовательно, множество
. Следовательно, множество  имеет верхнюю грань
имеет верхнюю грань  . По определению верхней грани
. По определению верхней грани  , т.е. множество всех верхних сумм ограничено снизу числом
, т.е. множество всех верхних сумм ограничено снизу числом  . Значит, множество
. Значит, множество  имеет нижнюю грань
имеет нижнюю грань 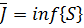 , причем
, причем  . Так что для любых
. Так что для любых  и
и 
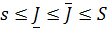
Величины  и
и  существуют для любой ограниченной функции
существуют для любой ограниченной функции  , определенной на
, определенной на  , в силу свойств сумм Дарбу.
, в силу свойств сумм Дарбу.  – нижний интеграл Дарбу,
– нижний интеграл Дарбу,
 - верхний интеграл Дарбу для функции
- верхний интеграл Дарбу для функции  на
на  .
.
89. Существование определенного интеграла
Теорема 1. Для интегрируемости ограниченной функции на некотором отрезке необходимо и достаточно, чтобы выполнялось условие

Доказательство. Условие (1) означает, что  такое, что
такое, что
 для любого разбиения
для любого разбиения 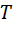 , удовлетворяющего условию
, удовлетворяющего условию  .
.
Необходимость. Пусть функция  интегрируема на
интегрируема на  , т.е
, т.е
 . Значит,
. Значит,  такое, что
такое, что  , если
, если  . Так, что
. Так, что 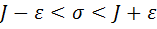 при
при  . Но для любого разбиения
. Но для любого разбиения 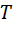 имеем
имеем 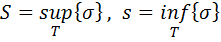 . Отсюда для любого
. Отсюда для любого 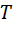 , удовлетворяющего условию
, удовлетворяющего условию  , будет
, будет  , т.е.
, т.е.  при
при  . Отсюда
. Отсюда 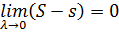 .
.
Достаточность. Пусть  ограничена и выполняется условие (1). Так как
ограничена и выполняется условие (1). Так как

то  . Величины
. Величины  и
и  от разбиения
от разбиения  не зависят. В силу (1) имеем из предыдущего неравенства
не зависят. В силу (1) имеем из предыдущего неравенства  . Обозначим их общее значение через
. Обозначим их общее значение через  . Тогда,
. Тогда,  откуда
откуда  для любого разбиения
для любого разбиения  , удовлетворяющего условию
, удовлетворяющего условию  . В силу (1)
. В силу (1)

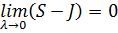 т.е.
т.е.

Так как для любого разбиения  , то
, то  , т.е.
, т.е.  интегрируема. Теорема доказана.
интегрируема. Теорема доказана.
Из (3) видим, что если  интегрируема на
интегрируема на  , то не только интегральные суммы
, то не только интегральные суммы  , но и суммы Дарбу
, но и суммы Дарбу  и
и  сходятся к интегралу
сходятся к интегралу  при
при  .
.
Определение 1. Разность  , где
, где 
 называется колебанием функции
называется колебанием функции  , определенной и ограниченной на
, определенной и ограниченной на  .
.
Пусть дано разбиение  сегмента
сегмента  . Колебание функции
. Колебание функции  на частичном сегменте
на частичном сегменте 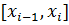 обозначим через
обозначим через 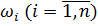 . Тогда
. Тогда
 . Так что условие (1) равносильно условию
. Так что условие (1) равносильно условию

90. Некоторые классы интегрируемых функций
Теорема 1. Если функция  непрерывна на
непрерывна на  , то она интегрируема на
, то она интегрируема на  .
.
Доказательство. Из непрерывности функции  на
на  следует ее ограниченность на
следует ее ограниченность на  (§35, теорема Вейерштрасса) и равномерная непрерывность на
(§35, теорема Вейерштрасса) и равномерная непрерывность на  (§37, теорема Кантора), т.е.
(§37, теорема Кантора), т.е.  такое, что для любой пары точек
такое, что для любой пары точек  и
и  из
из  ,
,  , выполняется неравенство
, выполняется неравенство
 .
.
Пусть  – любое разбиение
– любое разбиение  ,
,  . Так как
. Так как  непрерывна на
непрерывна на  , то на каждом частичном сегменте
, то на каждом частичном сегменте 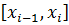 она достигает наибольшего и наименьшего значений, т.е. на
она достигает наибольшего и наименьшего значений, т.е. на 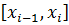
 и
и  что
что  ,
, 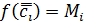
 .
.
Так как  , то
, то  ,т.е.
,т.е.

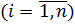 . Тогда
. Тогда 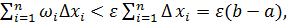 т.е.
т.е.  . Теорема доказана.
. Теорема доказана.
Теорема 2. Если определенная и ограниченная на  функция
функция  имеет лишь конечное число точек разрыва, то функция интегрируема на
имеет лишь конечное число точек разрыва, то функция интегрируема на  .
.
Иногда интегрируемы функции, имеющие даже бесконечно много точек разрыва.
Теорема 3. Если функция  определена и монотонна (в широком смысле) на
определена и монотонна (в широком смысле) на  , то она интегрируема на
, то она интегрируема на  .
.
Доказательство. Пусть для определенности  не убывает на
не убывает на  . Тогда
. Тогда  ,
,  , т.е.
, т.е.  ограничена на
ограничена на  .
.
Пусть  – произвольное разбиение
– произвольное разбиение  ,
,  . Так как
. Так как  ,
,  , то
, то  .
.


 . Таким образом
. Таким образом  . Теорема доказана.
. Теорема доказана.
Теперь можно построить пример функции с бесконечным числом точек разрыва, которая будет интегрируемой.
Пусть 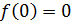 ,
,  при
при  . Она монотонна на
. Она монотонна на 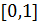 и имеет разрывы в точках
и имеет разрывы в точках  . По теореме 3 эта функция интегрируема на
. По теореме 3 эта функция интегрируема на 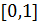 .
.
Не всякая ограниченная функция интегрируема!
Например, функция Дирихле 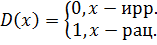 не интегрируема ни на каком сегменте. При любом разбиении имеем
не интегрируема ни на каком сегменте. При любом разбиении имеем  , т.е
, т.е 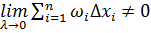 .
.
91. Свойства определенного интеграла
1) До сих пор в  мы считали
мы считали  .
.
Определение 1. Для любой функции  положим
положим  , а для функции, интегрируемой на
, а для функции, интегрируемой на  ,
,  .
.
В  считаем, что отрезки
считаем, что отрезки 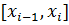 «измеряются» в отрицательном направлении. Тогда интегральные суммы для
«измеряются» в отрицательном направлении. Тогда интегральные суммы для  отличаются от интегральных сумм для
отличаются от интегральных сумм для  только знаком.
только знаком.
2) Если функция  интегрируема на
интегрируема на  , то она и на любом
, то она и на любом
 интегрируема.
интегрируема.
Доказательство. Так как  интегрируема на
интегрируема на  , то
, то  такое, что
такое, что  , если
, если  ,
,  – разбиение
– разбиение  . Пусть
. Пусть  – любое разбиение
– любое разбиение  ,
,  . Отрезки
. Отрезки  и
и  разобьем на части, длины которых
разобьем на части, длины которых  . Получим разбиение
. Получим разбиение  сегмента
сегмента  ,
,  . Для
. Для  будет
будет  . Аналогичная сумма для
. Аналогичная сумма для  состоит только из части слагаемых, т.е. для
состоит только из части слагаемых, т.е. для  тем более будет
тем более будет  .
.
3) Если функция  интегрируема на
интегрируема на  ,
,  - произвольная точка этого сегмента, то
- произвольная точка этого сегмента, то  .
.
Доказательство. Пусть  интегрируема на
интегрируема на  ,
,  - любое разбиение
- любое разбиение  ,
,  - точка деления. По свойству 2)
- точка деления. По свойству 2)  интегрируема на
интегрируема на  и
и 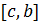 . Cоставим для
. Cоставим для  на
на  интегральную сумму
интегральную сумму  . Все слагаемые из
. Все слагаемые из  , соответствующие
, соответствующие  объединим в
объединим в  , остальные – в
, остальные – в  ,
,  . Перейдем к пределу:
. Перейдем к пределу:  , т.е.
, т.е. 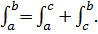 Если точка
Если точка  не является точкой деления разбиения
не является точкой деления разбиения  , то рассмотрим новое разбиение
, то рассмотрим новое разбиение  , полученное добавлением точки
, полученное добавлением точки  и рассуждаем аналогично.
и рассуждаем аналогично.
Свойство 3) называется свойством аддитивности определенного интеграла. Геометрически: площадь  равна сумме площадей
равна сумме площадей 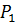 и
и  .
.
Замечание. Свойство 3) остается верным и тогда, когда точка  не лежит на
не лежит на  , а
, а  интегрируема на
интегрируема на  или
или 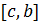 .
.
Действительно, пусть  ,
,  интегрируема на
интегрируема на  . По свойству 3)
. По свойству 3)  т.е.
т.е. 
4) Если функция  интегрируема на
интегрируема на  , то
, то 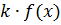 ,
,  , интегрируема на
, интегрируема на  и
и  .
.
Доказательство. Для функции 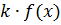 составим интегральную сумму
составим интегральную сумму 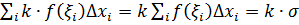 , где
, где  – интегральная сумма для
– интегральная сумма для  .
.
 .
.
5) Если функции  и
и  интегрируемы на
интегрируемы на  , то
, то  интегрируема на
интегрируема на  и
и  .
.
Доказательство.  - любое разбиение
- любое разбиение  ,
,  и
и  – интегральные суммы для
– интегральные суммы для  и
и  соответственно,
соответственно,  - интегральная сумма для
- интегральная сумма для  .
.
 ,
,  и
и 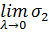 существуют. Значит существует и
существуют. Значит существует и  , т.е.
, т.е.  интегрируема на
интегрируема на  .
.
 .
.
6) Если  и интегрируема на
и интегрируема на  ,
,  , то
, то 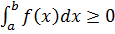 .
.
Доказательство. При любом  и любом выборе точек
и любом выборе точек 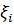 будет
будет
 , т.е.
, т.е.  , откуда
, откуда 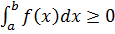 .
.
7) Если функции  и
и  интегрируемы на
интегрируемы на  ,
,  ,
, 
 , то
, то  .
.
Доказательство. Так как 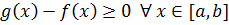 , то
, то
 , откуда
, откуда 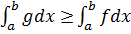 .
.
8) Если  интегрируема на
интегрируема на  ,
,  , то
, то  интегрируема на
интегрируема на  и
и  .
.
Доказательство. Так как  , то колебание
, то колебание  функции
функции  на
на 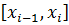 не превышает колебания
не превышает колебания  функции
функции  , т.е.
, т.е.  . Значит
. Значит  . Так как
. Так как  интегрируема на
интегрируема на  , то
, то  . Тогда
. Тогда  , т.е.
, т.е.  интегрируема на
интегрируема на  . Так как
. Так как 
 , то по свойству 7)
, то по свойству 7)
 , т.е.
, т.е.  .
.
92. Теорема о среднем значении
Теорема 1. Если функция  интегрируема на
интегрируема на  ,
,  и
и
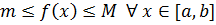 , то
, то

Доказательство. Из  по свойству 7)
по свойству 7) 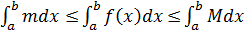 . Но
. Но  , так как здесь подынтегральная функция равна 1 и любая интегральная сумма
, так как здесь подынтегральная функция равна 1 и любая интегральная сумма  . Получаем (1). Теорема доказана.
. Получаем (1). Теорема доказана.
Теорема 2. (О среднем значении). Если  интегрируема на
интегрируема на  ,
,
 , то
, то  , где
, где  .
.
Доказательство. Если  , то, поделив (1) на
, то, поделив (1) на  , получим
, получим
 . Среднюю часть обозначим через
. Среднюю часть обозначим через  . Тогда
. Тогда 
и  .
.
Если  , то
, то  , т.е.
, т.е.  Теорема доказана.
Теорема доказана.
Пусть функция  непрерывна на
непрерывна на  ,
, 
 . По теореме о промежуточном значении непрерывной функции существует точка
. По теореме о промежуточном значении непрерывной функции существует точка 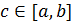 , в которой
, в которой  . Тогда
. Тогда
 .
.
Геометрически.  - площадь прямоугольника с основанием
- площадь прямоугольника с основанием  и высотой
и высотой  ,
,  - площадь криволинейной трапеции. Величина
- площадь криволинейной трапеции. Величина
 называется среднем значением непрерывной функции
называется среднем значением непрерывной функции  на
на  .
.
Теорема 3. Пусть функции  и
и  определены на
определены на  и
и
1)  и
и  интегрируемы на
интегрируемы на  ;
;
2)  не имеет знак на
не имеет знак на  , т.е. либо
, т.е. либо  , либо
, либо 
 ;
;
3)  .
.
Тогда  ,
,  , что
, что 
Доказательство. Для определенности пусть  ,
,