Системы счисления
Системой счисления называется способ записи чисел при помощи ограниченного числа символов (цифр).
Позиционные системы счисления
Позиционной системой счисления называется система счисления, при которой число, связанное с цифрой, зависит от места, которое она занимает.
Позиционные системы счисления — это те системы счисления, в которых значение цифры напрямую зависит от её положения в числе. Например, число 01 обозначает единицу, 10 — десять.
Чем хороши позиционные системы счисления? Тем, что они позволяют легко производить арифметические расчёты. Попробуйте считать используя, скажем, римские цифры. Сколько будет  ? То-то, а вот достаточно представить эти числа арабскими цифрами и мы легко сможем посчитать в столбик
? То-то, а вот достаточно представить эти числа арабскими цифрами и мы легко сможем посчитать в столбик  .
.
Представление чисел с помощью арабских цифр — самая распространённая позиционная система счисления, она называется «десятичной системой счисления». Десятичной системой она называется потому, что использует десять цифр. Вот эти цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Внимательно их пересчитайте — их ровно десять. Заметьте: максимальная цифра (9) на единичку меньше количества цифр (10).
Компьютер, в отличие от человека, хорошо разбирается в двоичной системе, он использует цифры: 0 и 1. Обратите внимание, что здесь система двоичная, а максимальная цифра 1.
Программисты пользуются, для упрощения себе жизни, ещё восьмеричной и шестнадцатеричной системами счисления.
Количество цифр используемых в системе счисления называется «основанием». В десятичной системе основание равно десяти, в двоичной системе основание равно двум, ну а в восьмеричной и шестнадцатеричной соответственно восьми и шестнадцати. То есть в р-ичной системе счисления количество цифр равно р и используются цифры от 0 до р-1.
В общем случае в позиционной системе счисления числа представляются следующим образом: (anan − 1... a 0) f, где a 0, a 1,..., an — цифры, а f — основание системы счисления. Если используется десятичная система, то f — можно опустить.
Примеры чисел:
- 110012 — число в двоичной системе счисления, a 0 = 1, a 1 = 0, a 2 = 0, a 3 = 1, a 4 = 1;
- 2213 — число в троичной системе счисления, a 0 = 1, a 1 = 2, a 2 = 2;
- 318 — число в восьмеричной системе счисления, a 0 = 1, a 1 = 3;
- 2510 — число в десятичной системе счисления, a 0 = 5, a 1 = 2;
Зависимость плотности записи информации от основания системы счисления
· Выражается функцией y=(ln(x))/x. Функция имеет максимум при x=e=2,718281828…. Из целочисленных систем счисления наибольшей плотностью записи информации обладает троичная система счисления с основанием равным трём. Эту задачу решали ещё во времена Непера, в результате для уменьшения таблиц и числа вычислений перешли к таблицам натуральных логарифмов с основанием равным числу Эйлера е=2,718281828….
Преобразование чисел
Такое представление чисел обозначает вот такое число: anfn +... + a 1 f 1 + a 0 f 0, где a 0, a 1,..., an — цифры, а f — основание системы счисления. Посмотрим, чему равны числа из примеров. Используем только что приведённую формулу:

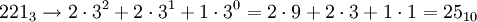 ;
;
 ;
;
 .
.
Мы разобрали, как узнать, чему равно число в любой системе счисления. Но как нам получить это число? Представим, что у нас есть некоторое число A, и мы хотим получить его представление в системе по основанию f. Как нам это сделать?
Мы знаем, что число A можно представить в виде (anan − 1... a 0) f, будем из этого исходить. Что будет, если мы поделим это число на f. Получим
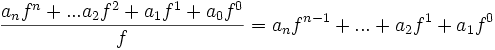
и остаток от деления a 0. Почему a 0? Все члены суммы делятся на f без остатка, а последний член a 0 в результате деления даёт 0 и a 0 в остатке, так как максимальное значение цифры всегда на единичку меньше основания системы.
Итак мы получили самую правую цифру a 0 как остаток от деления и число (anan − 1... a 1) f как результат деления числа A на f. Если мы так будем продолжать делить, то получим все цифры a 1, a 2... an.
Возьмём для примера полюбившееся нам число 25 и получим представление этого числа в двоичной системе счисления:
25 / 2 = 12, остаток 1;
12 / 2 = 6, остаток 0;
6 / 2 = 3, остаток 0;
3 / 2 = 1, остаток 1;
1 / 2 = 0, остаток 1.
Что и следовало ожидать, получили: 110012.
Десятичная система счисления:
· 25 / 10 = 2, остаток 5;
· 2 / 10 = 0, остаток 2.
Результат: 2510.
Чтобы ещё лучше понять перевод в различные системы счислений, посмотрим, какие трансформации происходят внутри числа 456710.
Представим это число в виде
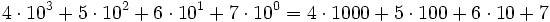 .
.
Посмотрим, что у нас получится при последовательном делении на 10:
- делим на 10, получаем
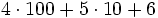 и 7 в остатке;
и 7 в остатке; - делим ещё раз на 10, получаем
 и 6 в остатке;
и 6 в остатке; - и ещё раз делим на 10, получаем 4 и 5 в остатке;
- делим в последний раз на 10, получаем 0 и 4 в остатке.
Представим число 25 в троичной системе счисления:
· 25 / 3 = 8, остаток 1;
· 8 / 3 = 2, остаток 2;
· 2 / 3 = 0, остаток 2.
Получили число: 2213.
Восьмеричная и шестнадцатеричная системы счислений
Компьютерам очень удобно оперировать двоичными числами, но люди не привыкли работать с большим количеством цифр. Например, чтобы представить в двоичном виде число 1234 потребуется больше 10 двоичных цифр (10011010010). Поэтому были придуманы восьмеричная и шестнадцатеричная системы счислений. Они удобны, как и десятичные числа тем, что для представления числа требуется меньшее количество разрядов. А по сравнению с десятичными числами, перевод в двоичное представление очень простой. Это как будто мы двоичное число разбили на группы по три или четыре разряда и каждой двоичной комбинации придумали значок.
Вот таблица для восьмеричных и шестнадцатеричных цифр:
| Таблица для восьмеричных и шестнадцатеричных цифр | ||
| Двоичная комбинация | для восьмеричных цифр | для шестнадцатеричных цифр |
| Значок | Значок | |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
Для закрепления наших знаний проделаем вычисления для восьмеричной и десятичной систем счисления.
Восьмеричная система счисления:
25 / 8 = 3, остаток 1;
3 / 8 = 0, остаток 3.
Результат: 318.
Перевод произвести очень просто, посмотрим на примере числа 10011010010.
Разбиваем его на группы по три цифры: 010 011 010 010. И по таблице переводим: 23228.
Чтобы перевести число в шестнадцатеричное представление разбиваем двоичное число на группы по четыре цифры: 0100 1101 0010. И по таблице переводим: 4 D 216.
В программистских кругах шестнадцатеричные числа принято предварять значком 0x (например, 0x4D2), такое написание пошло от языка программирования C, либо значком $ (например, $4D2), такая нотация произошла от языка программирования Pascal. Иногда в литературе используют буквы «h» и «b» для обозначения соответственно шестнадцатеричных и двоичных чисел (например, FFh или 1011b).
Вот таблица:
| Степень | Значение |
Произведём обратное преобразование. Чтобы преобразовать число в десятичном виде к двоичному, нам нужно будет делить всё время на два и смотреть на остаток от деления. Возьмём число 33.
https://digital.sibsutis.ru/digital/SysSchis.htm - системы счисления
Запись произвольного числа x в P -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена
x = anPn + an -1 Pn -1 +... + a 1 P 1 + a 0 P 0 + a -1 P -1 +... + a-mP-m
Примеры решения задач
1. Перевести данное число из десятичной системы счисления в двоичную:
а) 464(10); б) 380,1875(10); в) 115,94(10) (получить пять знаков после запятой в двоичном представлении).
Решение.
464 | 0 380 | 0 |1875 115 | 1 |94
232 | 0 190 | 0 0|375 57 | 1 1|88
116 | 0 95 | 1 0|75 28 | 0 1|76
58 | 0 47 | 1 1|5 14 | 0 1|52
а) 29 | 1 б) 23 | 1 1|0 в) 7 | 1 1|04
14 | 0 11 | 1 3 | 1 0|08
7 | 1 5 | 1 1 | 1 0|16
3 | 1 2 | 0
1 | 1 1 | 1
а) 464(10) = 111010000(2); б) 380,1875(10) = 101111100,0011(2); в) 115,94(10) » 1110011,11110(2) (в настоящем случае было получено шесть знаков после запятой, после чего результат был округлен).