Проекция вектора на ось. Проекция вектора на вектор

Тема: Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Скалярное произведение векторов.

Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава IV, § 3, п. 43-45, глава V, §2, п. 50-51), решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.

Теоретический минимум и задачи

Компланарные векторы.

Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.

Разложение вектора по трем некомпланарным векторам

Теорема. Любой вектор m может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых некомпланарных векторов а, b и с:

m = x a + y b + z c. (1)

Базисом пространства называются любые три некомпланарных вектора, взятые в определенном порядке.

Пусть e ₁, e ₂ и e ₃ — некоторый базис, и a — произвольный вектор. Тогда, по теореме, существуют три числа х, у, z таких, что

а = х e ₁ + у e ₂ + z e ₃.

Числа х, у и z называются координатами вектора а в данном базисе. В этом случае пишут а = (х; у; z).

Пример 1. Дано: ΔABC; А(1; 6; 2), 5(2; 3; -1), С(-3; 4; 5).

Разложить: 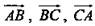по координатным векторам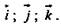

Решение:

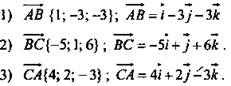
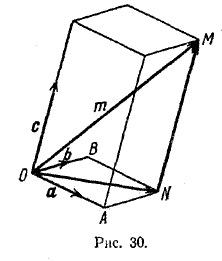
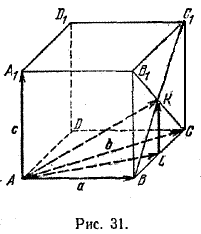Пример 2. Дан куб ABCDA₁B₁C₁D₁. Разложить вектор AK ^>, где K — центр грани ВСС₁В₁ по векторам а = AB ^>, b = AC ^>, с = AA ₁^>.

Из /\ AKL имеем AK ^> = AL ^> + LK ^>, но

Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины.

Угол между векторами на плоскости и в пространстве.

Пусть на плоскости или в трехмерном пространстве заданы два ненулевых вектора и 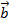. Отложим от произвольной точки O векторы 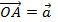и 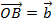. Тогда справедливо следующее определение.

Определение.

Углом между векторами и называется угол между лучами OA и OB.

Угол между векторами и 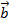будем обозначать как .

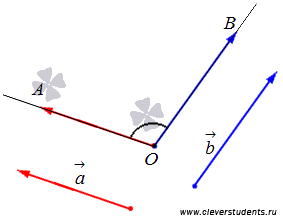
Понятно, что угол между векторами может принимать значения от 0 до 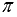или, что то же самое, от 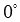до .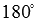

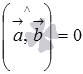когда векторы 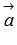и 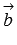сонаправленные, 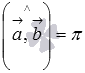когда векторы 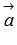и 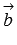противоположно направленные.

Определение.

Векторы 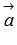и 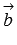называются перпендикулярными, если угол между ними равен 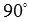( 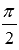радиан).

Если хотя бы один из векторов 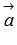и 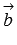нулевой, то угол 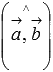не определен.

Скалярное произведение векторов

Скалярным произведением векторов 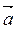(аx; y; z) ∙ 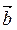(bx; by; bz) называется число (скаляр) 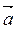· 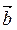= аx · bx + аy· by + аz · bz.

Решение задач

1. Найдите 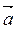· 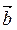, если 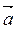(-2; 3; 1), 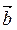(-4; -5; 2).

2. Даны векторы 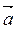(2; -1; 4), 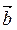(5; 3; n). При каком значении п скалярное произведение векторов равна -3?

Из определения скалярного произведения двух векторов 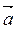и 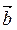вытекают его свойства.

1) · = · .

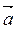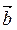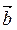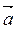2) ( + ) · = · + · .

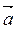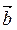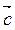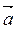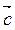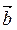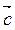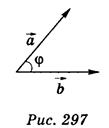3) Скалярное произведение векторов 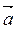и 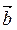равно произведению их абсолютных величин на косинус угла между ними: 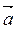· 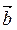= | | 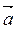· | | 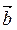cos φ.

1)

2) Две отличные от нуля векторы 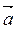и 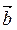перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Пример При каком значении 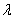векторы 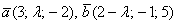будут ортогональны?

Решение: По условию требуется найти такое значение параметра 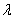, чтобы данные векторы были ортогональны. Два вектора пространства ортогональны тогда и только тогда, когда 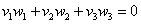. Составим уравнение:

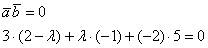
Раскрываем скобки и приводим подобные слагаемые:

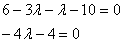
Решаем уравнение:

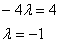
Ответ: при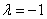

Проекция вектора на ось. Проекция вектора на вектор

Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A₁B₁ оси l, где точки A₁ и B₁ являются проекциями точек A и B на ось l.

Определение.

Проекцией вектора a на направление вектора b, называется число, равное величине проэкции вектора a на ось проходящую через вектор b.