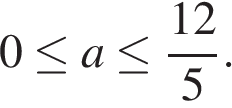Задание 18 № 519639
Найдите все значения а, при каждом из которых множество решений неравенства
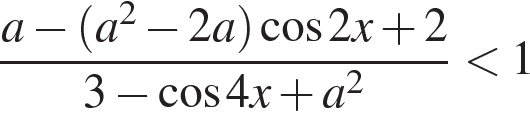
содержит отрезок 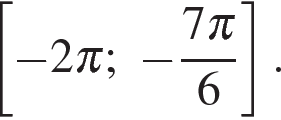
Решение.
Заметим, что при любых значениях переменной  и параметра
и параметра 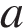 знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству
знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству
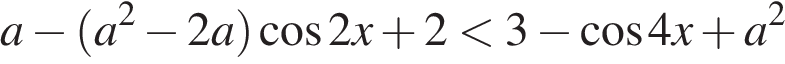
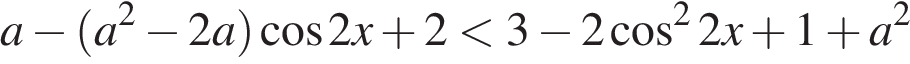
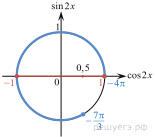
Для того, чтобы множество решений неравенства содержало отрезок 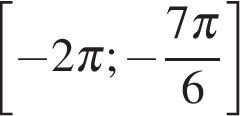 , удвоенный аргумент должен содержать отрезок
, удвоенный аргумент должен содержать отрезок 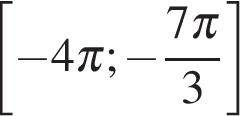 , а косинус двойного угла должен принимать все значения
, а косинус двойного угла должен принимать все значения  (см. рисунок)
(см. рисунок)
Пусть  , тогда неравенство принимает вид
, тогда неравенство принимает вид
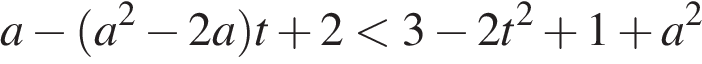
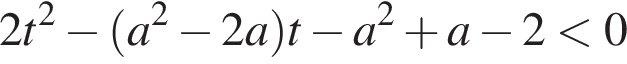
Рассмотрим функцию 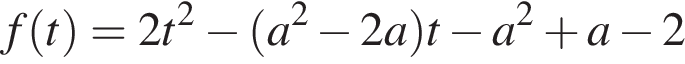
Для того, чтобы множество решений последнего неравенства содержало отрезок 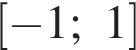 необходимо и достаточно, чтобы одновременно выполнялись два условия
необходимо и достаточно, чтобы одновременно выполнялись два условия 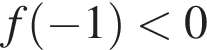 и
и 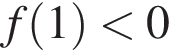
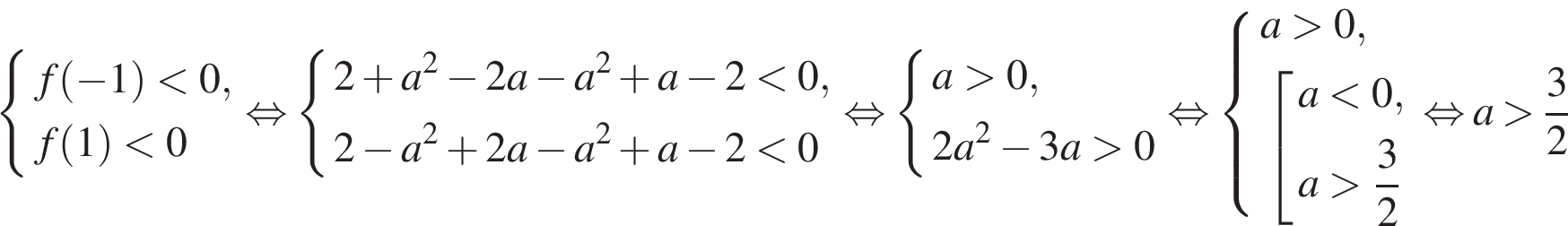
Ответ: 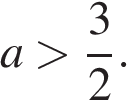
Задание 18 № 516765
Найдите все такие значения параметра a, при каждом из которых уравнение 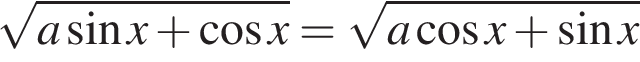 имеет решения на отрезке
имеет решения на отрезке 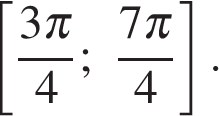
Решение.
Заметим, что
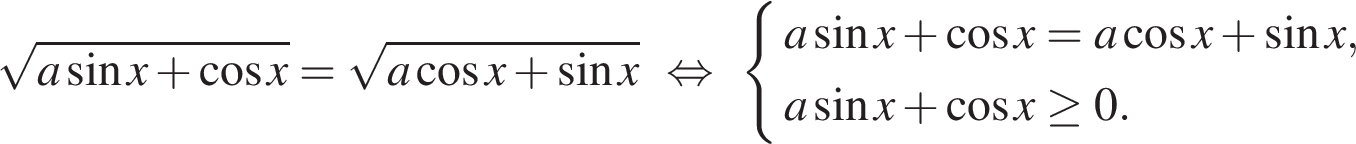
Преобразуем уравнение:
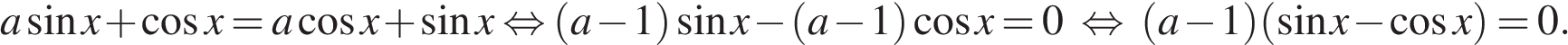
Рассмотрим два случая.
Пусть  , тогда из неравенства:
, тогда из неравенства:
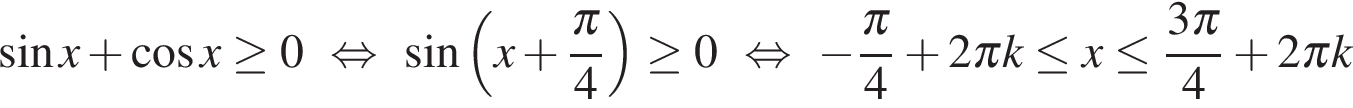
Отрезку 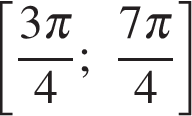 принадлежат два числа
принадлежат два числа 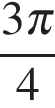 и
и 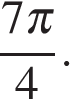
Пусть 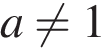 , тогда имеем:
, тогда имеем:
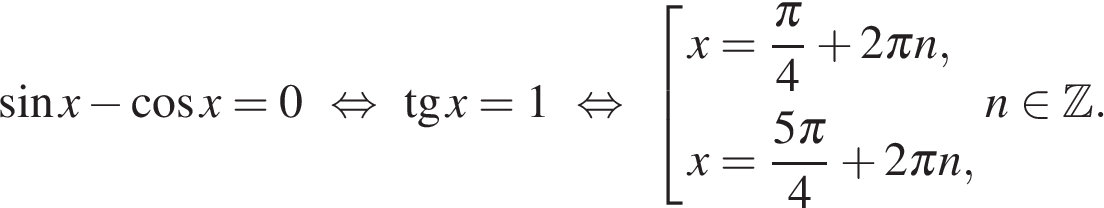
В первой серии не содержится корней, лежащих на отрезке 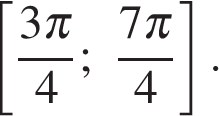 Среди корней, содержащихся во второй серии, отрезку
Среди корней, содержащихся во второй серии, отрезку 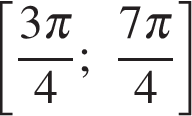 принадлежит одно число
принадлежит одно число 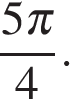 Подставляя его в неравенство, получаем:
Подставляя его в неравенство, получаем: 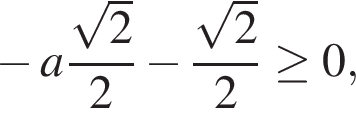 откуда
откуда 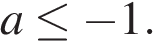
Ответ:  ,
, 
51. Задание 18 № 529302 перебор случаев
Найдите все значения параметра a, при которых уравнение
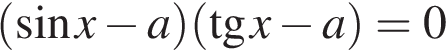
имеет единственное решение на интервале 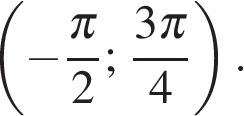
Решение.
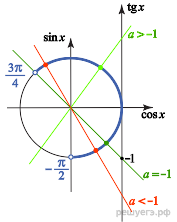
Исходное уравнение равносильно совокупности
Уравнение  на интервале
на интервале  при
при  имеет один корень, при
имеет один корень, при 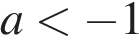 имеет два корня (см. верхний рисунок).
имеет два корня (см. верхний рисунок).
Система
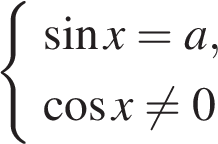
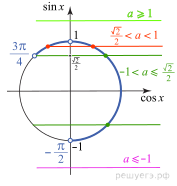
на интервале  при
при  не имеет корней, при
не имеет корней, при 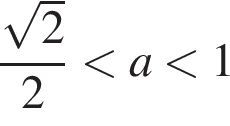 имеет два корня, при
имеет два корня, при 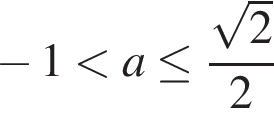 имеет один корень, при
имеет один корень, при  не имеет корней (см. нижний рисунок).
не имеет корней (см. нижний рисунок).
|
|
Выясним, при каких значениях a корни уравнений 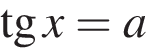 и
и 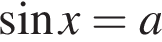 совпадают. Для этого решим уравнение
совпадают. Для этого решим уравнение 

Значит, корни уравнений 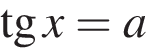 и
и 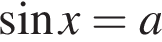 совпадают только при
совпадают только при 
Суммируя все случаи, получаем, что исходное уравнение на интервале 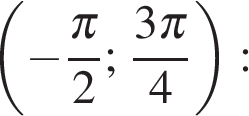
— при  имеет один корень;
имеет один корень;
— при 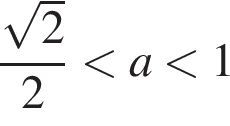 — три корня;
— три корня;
— при 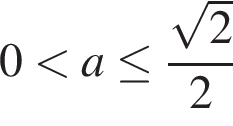 — два корня;
— два корня;
— при  — один корень;
— один корень;
— при 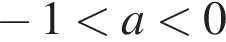 — два корня;
— два корня;
— при 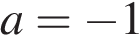 — один корень;
— один корень;
— при  — два корня.
— два корня.
Ответ: 
Задание 18 № 505782
Найдите все значения параметра a, при которых функция
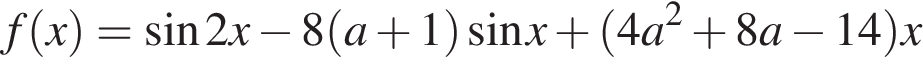
является возрастающей на всей числовой прямой и при этом не имеет критических точек.
Решение.
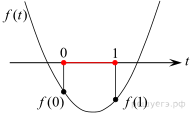
Возьмем производную этой функции (она должна быть всюду положительна).

Обозначим 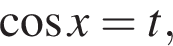
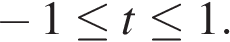
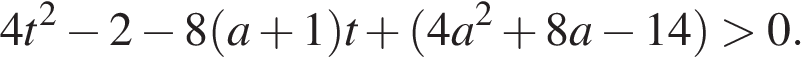
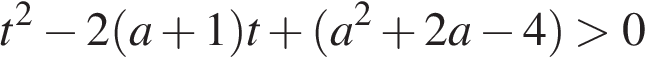
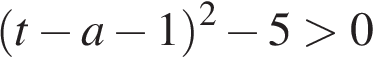
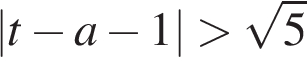
Это неравенство должно выполняться при всех t из отрезка 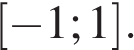
Если  то неравенство не выполняется, например, при
то неравенство не выполняется, например, при 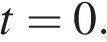
Если  то
то  при всех t из отрезка
при всех t из отрезка  и
и  поэтому нужно, чтобы
поэтому нужно, чтобы 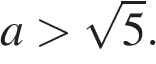
Если 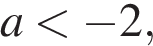 то
то  при всех t из отрезка
при всех t из отрезка  и
и  поэтому нужно, чтобы
поэтому нужно, чтобы 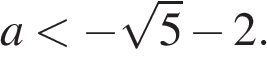
Ответ: 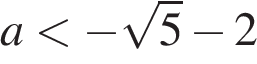 или
или 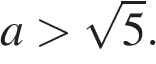
Задание 18 № 505988
Найти все значения параметра 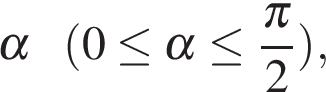 при каждом из которых наименьшее значение функции
при каждом из которых наименьшее значение функции 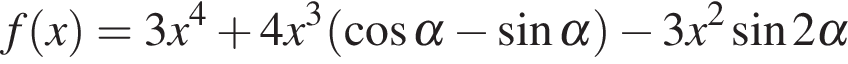 на отрезке
на отрезке 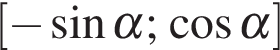 принимает наименьшее значение.
принимает наименьшее значение.
Решение.
Наименьшее значение эта функция принимает либо в нулях производной, либо в одном из концов отрезка. Найдем производную:
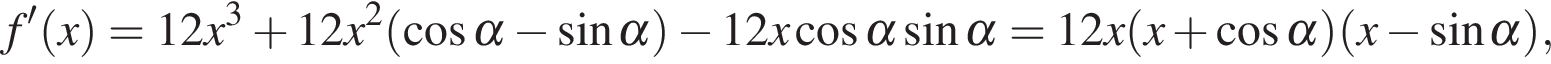
поэтому нули производной равны 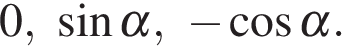
Если  то производная имеет вид
то производная имеет вид 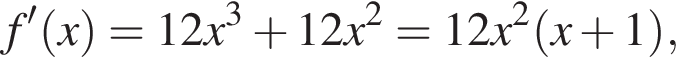 корни производной суть числа 0 и −1. Отрезок
корни производной суть числа 0 и −1. Отрезок 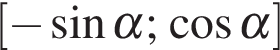 становится отрезком [0; 1], на нем функция f возрастает. Наименьшее значение достигается на левой границе отрезка. (*)
становится отрезком [0; 1], на нем функция f возрастает. Наименьшее значение достигается на левой границе отрезка. (*)
Если 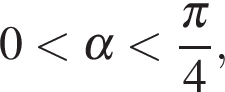 то
то 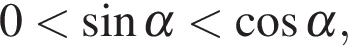 а
а  не лежит на отрезке
не лежит на отрезке 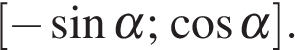 В этом случае имеем следующее расположение знаков производной:
В этом случае имеем следующее расположение знаков производной:
| Интервал | (
| 
| (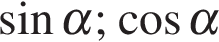 ) )
|
знак 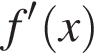
| + | − | + |
|
|
Наименьшего значения функция достигает либо на левой границе отрезка, либо в точке 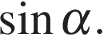 (**)
(**)
Если  то производная имеет вид
то производная имеет вид 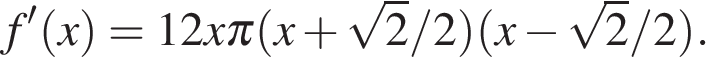 Отрезок
Отрезок 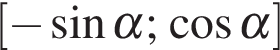 становится отрезком
становится отрезком 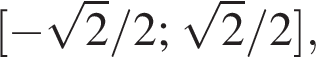 на нем функция лежит единственный корень производной — число 0. Это точка максимума, поэтому наименьшее значение достигается или на левой границе отрезка, или на правой границе. Эти значения равны, будем считать, что наименьшее значение достигается на левой границе (***).
на нем функция лежит единственный корень производной — число 0. Это точка максимума, поэтому наименьшее значение достигается или на левой границе отрезка, или на правой границе. Эти значения равны, будем считать, что наименьшее значение достигается на левой границе (***).
Объединяя случаи (*), (**) и (***) получаем, что если 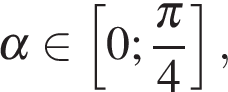 то ее наименьшее значение равно наименьшему из значений
то ее наименьшее значение равно наименьшему из значений 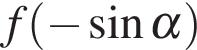 и
и  Имеем:
Имеем:
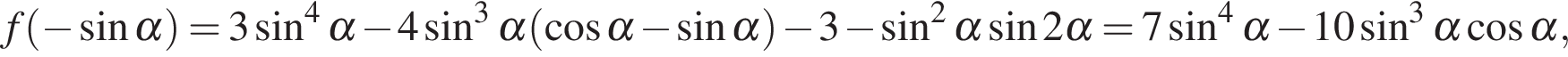
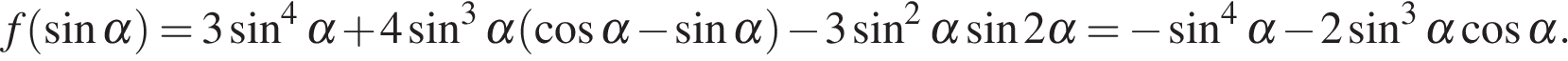
Рассмотрим разность найденных значений на отрезке 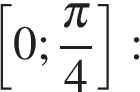
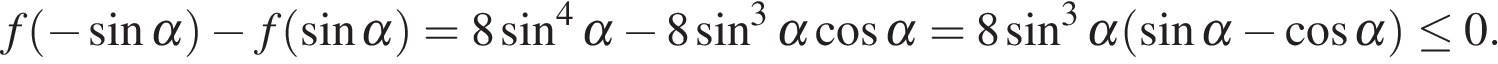
Поэтому
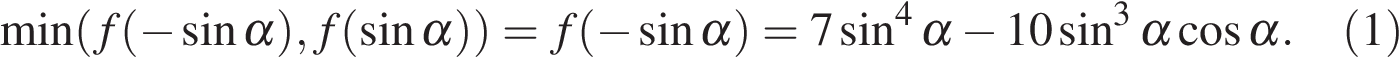
Если 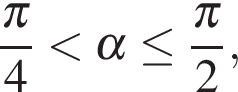 то
то  а
а  не лежит на указанном отрезке. Рассуждая аналогично, находим, что если
не лежит на указанном отрезке. Рассуждая аналогично, находим, что если  то функция убывает на
то функция убывает на 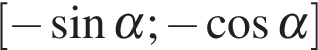 и на
и на  Проведя аналогичные вычисления, можно получить, что ее наименьшее значение равно
Проведя аналогичные вычисления, можно получить, что ее наименьшее значение равно
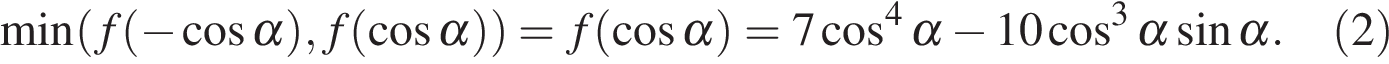
Осталось исследовать наименьшие значения (1) и (2) на соответствующих отрезках и найти наименьшее из них. Однако поскольку при замене  функции переходят друг в друга, достаточно будет исследовать одну из них. Иными словами, поскольку для всех α из отрезка
функции переходят друг в друга, достаточно будет исследовать одну из них. Иными словами, поскольку для всех α из отрезка  верно равенство
верно равенство 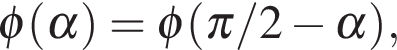 достаточно найти наименьшее значение функции
достаточно найти наименьшее значение функции 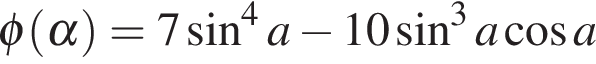 на промежутке
на промежутке 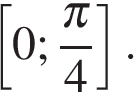
Исследуем производную функции на интервале 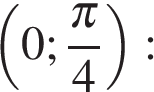

Решениями уравнения 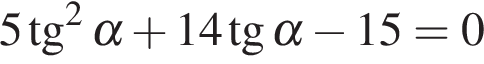 являются числа
являются числа 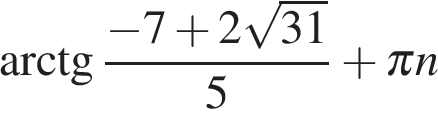 и
и 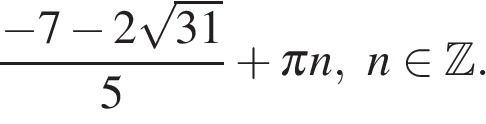 На интервале
На интервале 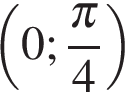 значения тангенса положительны и меньше 1, поэтому в него входит только корень
значения тангенса положительны и меньше 1, поэтому в него входит только корень 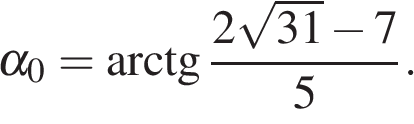
На интервале 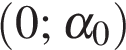 производная
производная 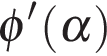 отрицательна, на интервале
отрицательна, на интервале 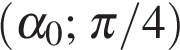 положительна. Следовательно, функция
положительна. Следовательно, функция  убывает на отрезке
убывает на отрезке 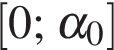 и возрастает на отрезке
и возрастает на отрезке 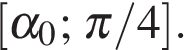 Поэтому наименьшее значение
Поэтому наименьшее значение  на отрезке
на отрезке 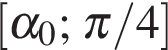 достигается в точке
достигается в точке 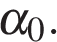 Такое же наименьшее значение
Такое же наименьшее значение  принимает и в точке
принимает и в точке 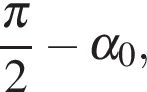 принадлежащей отрезку
принадлежащей отрезку 
|
|
Итак, наименьшее значение достигается в точках 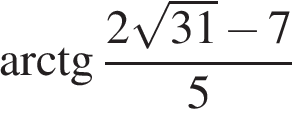 и
и 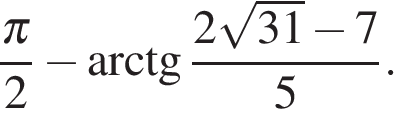
Примечение РЕШУ ЕГЭ.
Это задание из вступительного экзамена в Московский государственный университет несколько сложнее других.
Задание 18 № 519644
Найдите все значения параметра a, при каждом из которых множество значений функции 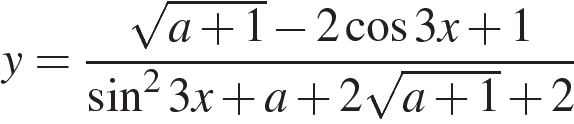 содержит отрезок
содержит отрезок 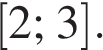
Решение.
Пусть 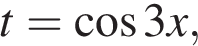 тогда
тогда 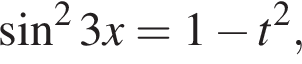 причем
причем  Пусть, далее,
Пусть, далее, 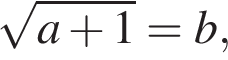 тогда
тогда  и
и 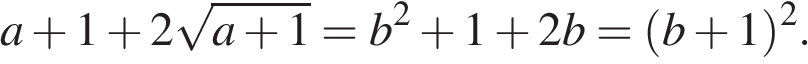 Обозначим, наконец,
Обозначим, наконец, 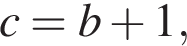 и заметим, что в силу неотрицательности b справедливо неравенство
и заметим, что в силу неотрицательности b справедливо неравенство  Исходная задача свелась к следующей: необходимо найти все значения параметра с, при каждом из которых множество значений функции
Исходная задача свелась к следующей: необходимо найти все значения параметра с, при каждом из которых множество значений функции 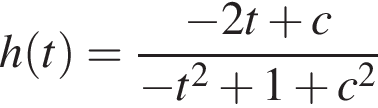 при
при  содержит отрезок [2; 3].
содержит отрезок [2; 3].
Заметим, что разность  неотрицательна при
неотрицательна при 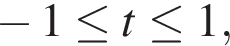 а значит, знаменатель дроби не меньше 1. Следовательно, функция
а значит, знаменатель дроби не меньше 1. Следовательно, функция 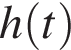 непрерывна, а тогда отрезок [2; 3] лежит во множестве ее значений тогда и только тогда, когда уравнения
непрерывна, а тогда отрезок [2; 3] лежит во множестве ее значений тогда и только тогда, когда уравнения 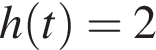 и
и 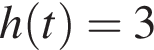 имеют решения, удовлетворяющие условию
имеют решения, удовлетворяющие условию 
Рассмотрим эти уравнения:
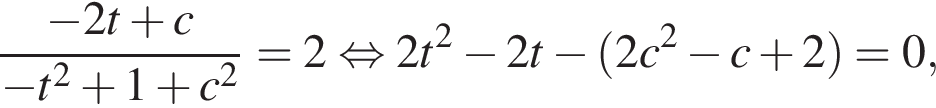
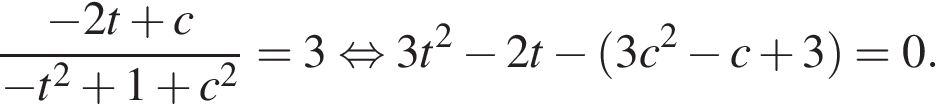
Поскольку  справедливы оценки:
справедливы оценки: 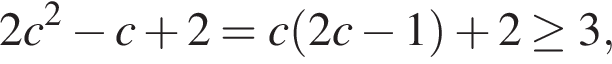
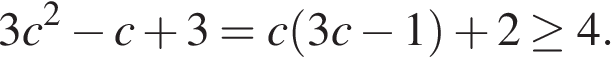 Тем самым, свободные члены квадратных трехчленов
Тем самым, свободные члены квадратных трехчленов 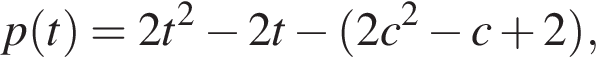 и
и 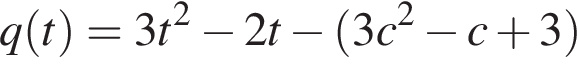 отрицательны, а значит, их графики пересекают ось ординат в точках с отрицательной абсциссой. Ветви соответствующих парабол направлены вверх, их вершины лежат ниже оси абсцисс на прямых
отрицательны, а значит, их графики пересекают ось ординат в точках с отрицательной абсциссой. Ветви соответствующих парабол направлены вверх, их вершины лежат ниже оси абсцисс на прямых 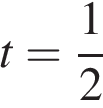 и
и 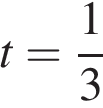 соответственно. Из этого следует, что указанные параболы будут пересекать отрезок
соответственно. Из этого следует, что указанные параболы будут пересекать отрезок 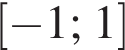 оси абсцисс хотя бы в одной точке тогда и только тогда, когда
оси абсцисс хотя бы в одной точке тогда и только тогда, когда 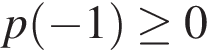 и
и 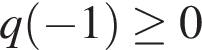 одновременно. Имеем:
одновременно. Имеем:
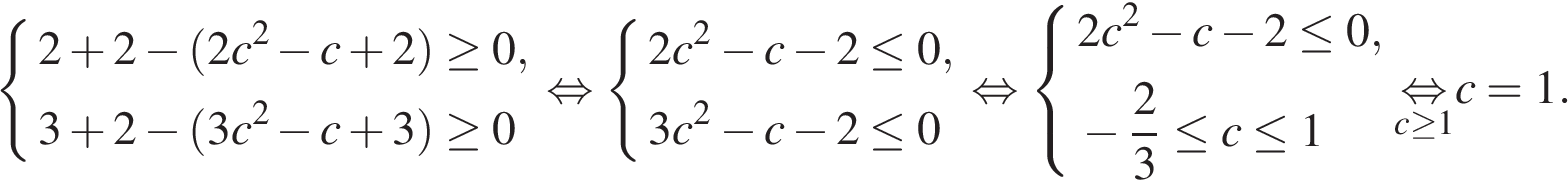
Тогда  откуда
откуда 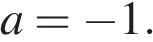
Ответ: a = −1.
Задание 18 № 519682
Найдите все значения a, при каждом из которых для любой пары 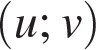 действительных чисел u и v выполнено неравенство
действительных чисел u и v выполнено неравенство

Решение.
Пусть 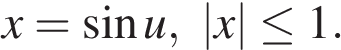 Имеем:
Имеем:
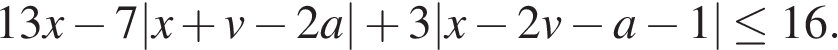
При фиксированных v и a рассмотрим левую часть как функцию от x:
В зависимости от того, как располагается x относительно точек 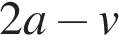 и
и 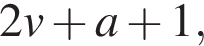 модули раскроются по-разному. При этом на каждом участке непрерывная функция f(x) будет линейной с угловым коэффицентом
модули раскроются по-разному. При этом на каждом участке непрерывная функция f(x) будет линейной с угловым коэффицентом 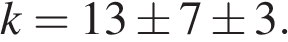 Какова бы ни была комбинация знаков,
Какова бы ни была комбинация знаков,  Следовательно, f(x) монотонно возрастает. Поэтому неравенство
Следовательно, f(x) монотонно возрастает. Поэтому неравенство 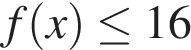 выполняется при всех
выполняется при всех 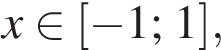 если и только если
если и только если 
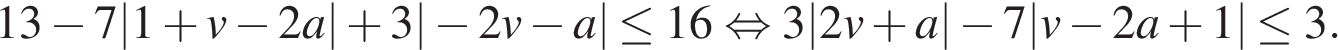
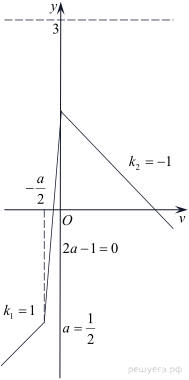
При малых v, то есть меньших, чем наименьшее из чисел 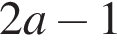 и
и 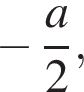 функция
функция 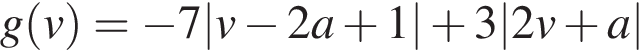 — возрастающая линейная с угловым коэффицентом
— возрастающая линейная с угловым коэффицентом  При больших v, то есть больших, чем максимум из тех же чисел, g(v) — убывающая линейная функция с угловым коэффицентом
При больших v, то есть больших, чем максимум из тех же чисел, g(v) — убывающая линейная функция с угловым коэффицентом  (см. рис.). Поэтому функция g(v) принимает наибольшее значение в одной из точек
(см. рис.). Поэтому функция g(v) принимает наибольшее значение в одной из точек 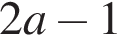 или
или 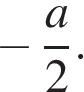 Неравенство
Неравенство 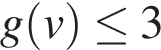 выполняется при всех v тогда и только тогда, когда
выполняется при всех v тогда и только тогда, когда 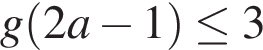 и
и 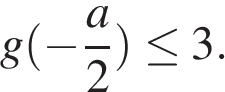 Получаем:
Получаем:
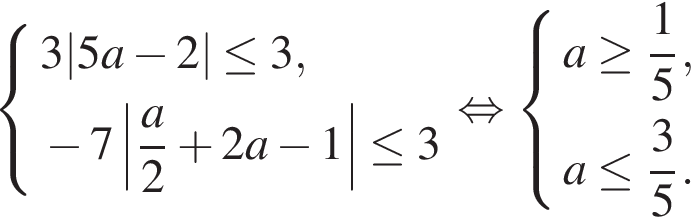
Ответ: 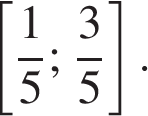
Задание 18 № 526808
При каких значениях параметра a область значений функции
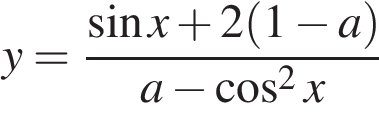
содержит отрезок [1; 2]?
Решение.
Полагая 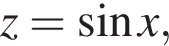
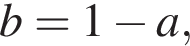 перепишем уравнение в виде:
перепишем уравнение в виде:

где 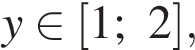 а
а 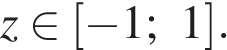 Дальнейшие рассуждения свяжем с соотношением
Дальнейшие рассуждения свяжем с соотношением
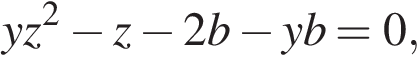
которое будем рассматривать как уравнение относительно переменной z. Это уравнение может иметь лишние корни, которые, если они существуют, будут выявлены в дальнейшем при рассмотрении системы
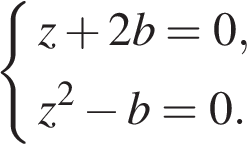
Имея это в виду, рассмотрим квадратный трёхчлен
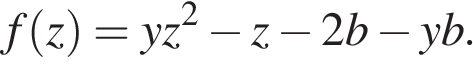
Тогда задачу можно переформулировать следующим образом: при каких значениях параметра b для любого  существует корень квадратного трёхчлена
существует корень квадратного трёхчлена  принадлежащий отрезку [−1; 1]?
принадлежащий отрезку [−1; 1]?
Заметим, что квадратный трёхчлен 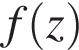 имеет корни только в случае, когда
имеет корни только в случае, когда 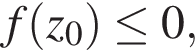 где
где  — абсцисса вершины параболы — графика рассматриваемого трёхчлена, с учётом того, что
— абсцисса вершины параболы — графика рассматриваемого трёхчлена, с учётом того, что 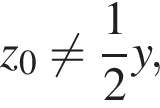 приходим к рассмотрению неравенства
приходим к рассмотрению неравенства
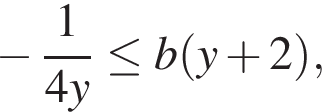
которое при  равносильно неравенству
равносильно неравенству
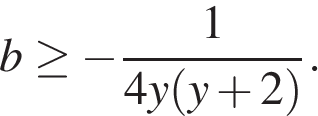
Если теперь рассмотреть функцию 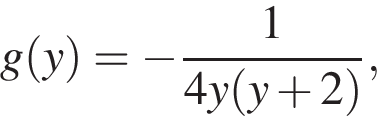 то так как
то так как 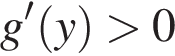 для
для 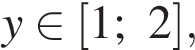 своё максимальное значение она принимает на правом конце рассматриваемого отрезка. А поскольку
своё максимальное значение она принимает на правом конце рассматриваемого отрезка. А поскольку
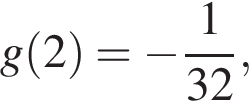
то неравенство 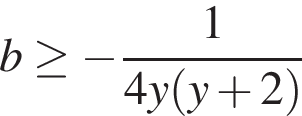 будет выполняться при всех
будет выполняться при всех 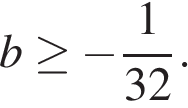 Следующий шаг в решении задачи состоит в том, чтобы среди найденных значений параметра b, при которых существуют корни уравнения
Следующий шаг в решении задачи состоит в том, чтобы среди найденных значений параметра b, при которых существуют корни уравнения 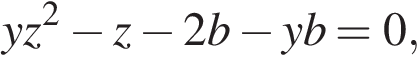 выбрать те значения, при которых хотя бы один из корней принадлежит отрезку [−1; 1].
выбрать те значения, при которых хотя бы один из корней принадлежит отрезку [−1; 1].
Но так как 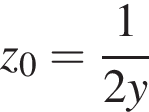 и
и  то
то 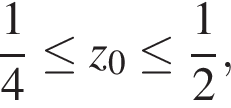 и поэтому хотя бы один корень квадратного трёхчлена
и поэтому хотя бы один корень квадратного трёхчлена 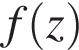 будет принадлежать отрезку [−1; 1] при тех значениях параметра b, при которых справедливо неравенство
будет принадлежать отрезку [−1; 1] при тех значениях параметра b, при которых справедливо неравенство 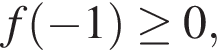 т. е. когда
т. е. когда
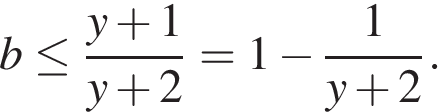
Функция 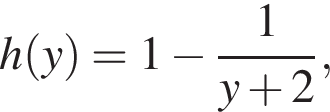 графиком которой является гипербола, принимает наименьшее своё значение на отрезке [1; 2], равное
графиком которой является гипербола, принимает наименьшее своё значение на отрезке [1; 2], равное  при
при  и поэтому
и поэтому 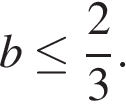
Объединяя полученные результаты, приходим к выводу, что
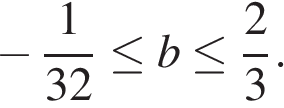
Рассмотрим теперь случай, когда в соотношении 
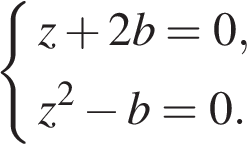
Решая эту систему, находим, что либо 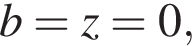 либо
либо 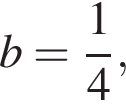
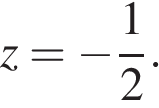 При
При  равенство
равенство  переписывается в виде
переписывается в виде
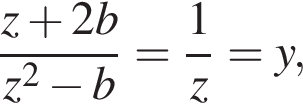
и значения  достигаются при значениях
достигаются при значениях 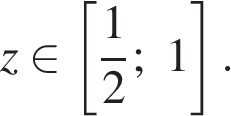 При
При 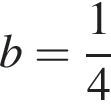 равенство
равенство  записывается в виде
записывается в виде
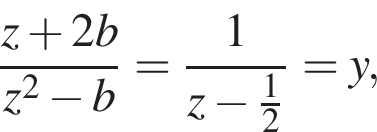
и значения  достигаются при значениях
достигаются при значениях 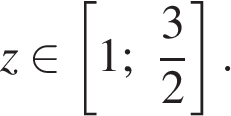 Но у нас
Но у нас 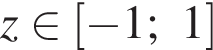 и, таким образом, значение
и, таким образом, значение 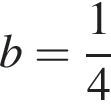 не удовлетворяет требованиям задачи. Итак,
не удовлетворяет требованиям задачи. Итак,
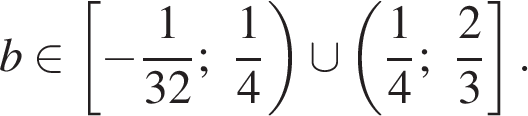
Возвращаясь к параметру a, получаем: 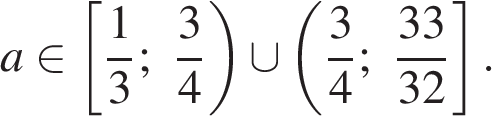
Ответ: 
14. Задание 18 № 484636 уравнение дкружности
При каких значениях а системы уравнении 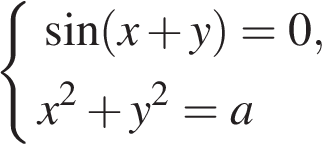 и
и 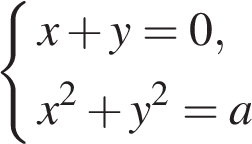 равносильны?
равносильны?
Решение.
При  ни одна из систем не имеет решений и, следовательно, они равносильны. При
ни одна из систем не имеет решений и, следовательно, они равносильны. При  второе уравнение, общее для обеих систем, имеет единственное решение
второе уравнение, общее для обеих систем, имеет единственное решение  ,
,  , удовлетворяющее и первым уравнениям обеих систем. Поэтому системы равносильны и при
, удовлетворяющее и первым уравнениям обеих систем. Поэтому системы равносильны и при 
При  второе уравнение задается окружностью радиуса
второе уравнение задается окружностью радиуса  с центром в начале координат. Уравнение
с центром в начале координат. Уравнение  равносильно бесконечной совокупности уравнений
равносильно бесконечной совокупности уравнений 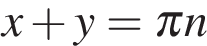 ,
, 
Системы равносильны тогда и только тогда, когда окружность, определяемая вторым уравнением, имеет общие точки только с прямой 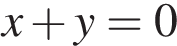 , соответствующей
, соответствующей  в первой системе. Для этого необходимо и достаточно, чтобы ее радиус был меньше, чем расстояние от начала координат до прямой
в первой системе. Для этого необходимо и достаточно, чтобы ее радиус был меньше, чем расстояние от начала координат до прямой  , т. е. чем число
, т. е. чем число 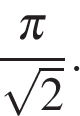
Итак, 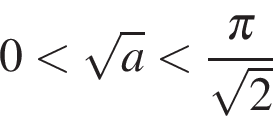 или
или 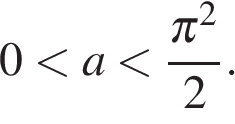 Добавляя полученные ранее значения
Добавляя полученные ранее значения  , получаем ответ.
, получаем ответ.
Ответ: 
Задание 18 № 530241
Найдите все значения параметра a, при которых система уравнений
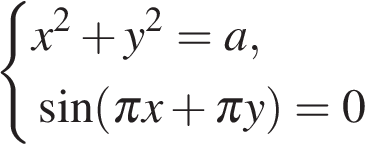
имеет ровно четыре решения.
Решение.
Преобразуем систему:
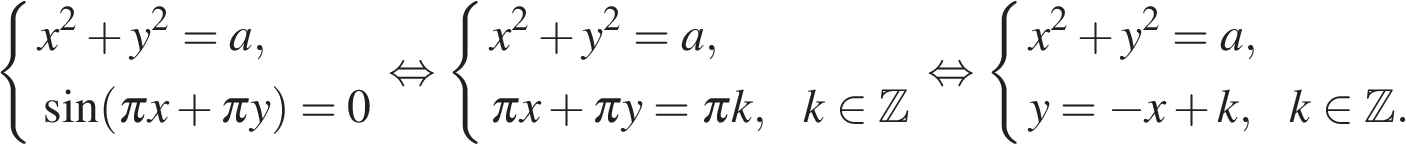
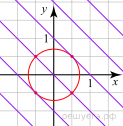
Графиком второго уравнения является семейство параллельных прямых (см. рис., выделено лиловым). При  первое уравнение, а значит, и вся система, не имеет решений. При
первое уравнение, а значит, и вся система, не имеет решений. При  графиком первого уравнения в системе координат xOy является окружность с центром в точке
графиком первого уравнения в системе координат xOy является окружность с центром в точке 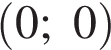 и радиусом
и радиусом  , при
, при  вырождающаяся в точку. При
вырождающаяся в точку. При  система имеет единственное решение
система имеет единственное решение 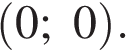 Исходная система будет иметь ровно четыре решения тогда и только тогда, когда окружность будет иметь ровно четыре общие точки с семейством прямых.
Исходная система будет иметь ровно четыре решения тогда и только тогда, когда окружность будет иметь ровно четыре общие точки с семейством прямых.
Прямая 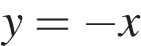 при любом значении
при любом значении  имеет две общие точки с окружностью. В силу симметрии прямая
имеет две общие точки с окружностью. В силу симметрии прямая  и прямая
и прямая  касаются окружности при одном и том же значении a. Радиус окружности в этом случае равен половине диагонали квадрата со стороной 1, то есть радиус равен
касаются окружности при одном и том же значении a. Радиус окружности в этом случае равен половине диагонали квадрата со стороной 1, то есть радиус равен 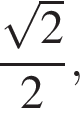 откуда
откуда 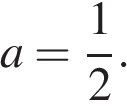 Значит, при
Значит, при 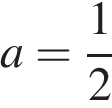 система имеет ровно четыре решения. При других значениях параметра система будет иметь или больше четырех решений, или меньше.
система имеет ровно четыре решения. При других значениях параметра система будет иметь или больше четырех решений, или меньше.
Ответ: 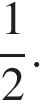
Задание 18 № 505710
Найти все значения параметра a, при каждом из которых неравенство
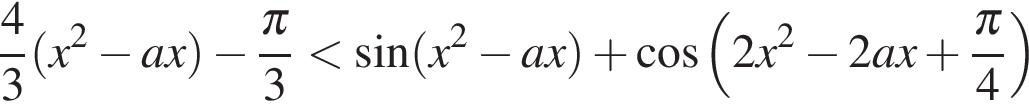
выполняется для всех x из отрезка 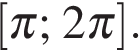
Решение.
Пусть 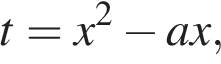 тогда
тогда 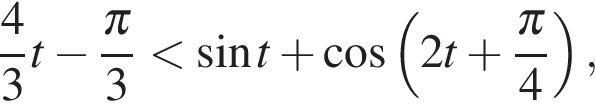 то есть
то есть 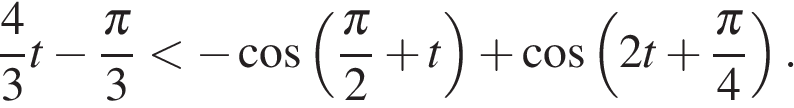 Проявив опыт и смекалку, запишем полученное неравенство в виде
Проявив опыт и смекалку, запишем полученное неравенство в виде
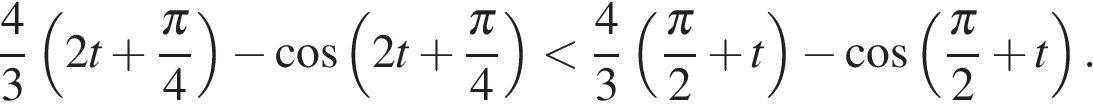
Полученное неравенство имеет вид 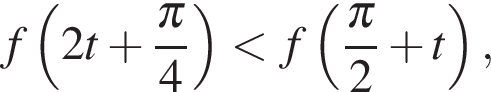 для
для 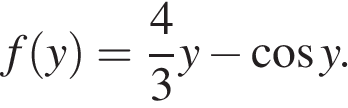 Поскольку
Поскольку 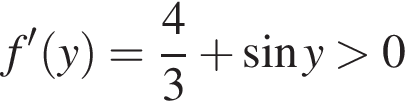 для всех y, функция f возрастающая. Следовательно, неравенство относительно значений функции можно заменить равносильным неравенством на аргументы. Тогда
для всех y, функция f возрастающая. Следовательно, неравенство относительно значений функции можно заменить равносильным неравенством на аргументы. Тогда 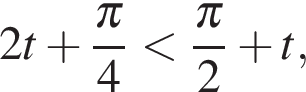 откуда
откуда 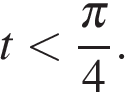
Возвращаясь к исходной переменной, получаем неравенство 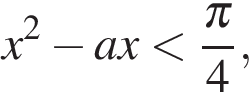 то есть
то есть 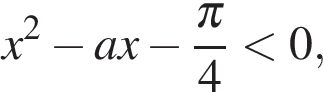 которое должно быть выполнено для всех х из отрезка
которое должно быть выполнено для всех х из отрезка 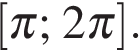 Старший коэффициент квадратного трехчлена
Старший коэффициент квадратного трехчлена 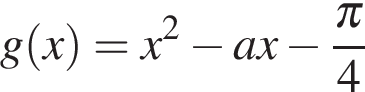 положителен, поэтому если значения g на концах отрезка отрицательны, то и на всем отрезке отрицательны. Получаем систему:
положителен, поэтому если значения g на концах отрезка отрицательны, то и на всем отрезке отрицательны. Получаем систему:
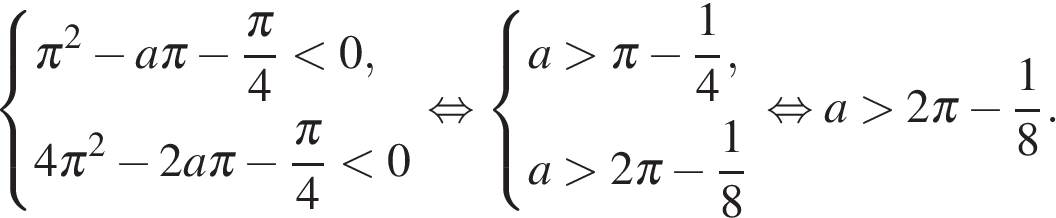
Ответ: 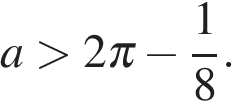
Приведем другое решение.
Введя замену 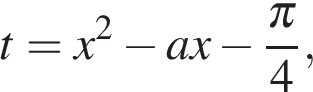 получим неравенство
получим неравенство 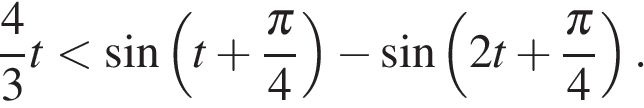 Запишем это неравенство в виде
Запишем это неравенство в виде 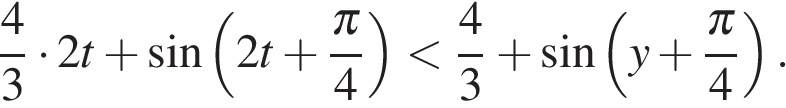 Этим задача сведена к неравенству
Этим задача сведена к неравенству 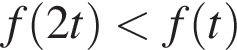 для возрастающей функции
для возрастающей функции 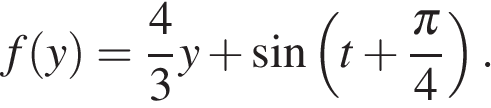 Тем самым
Тем самым 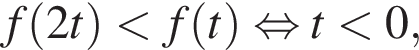 откуда
откуда 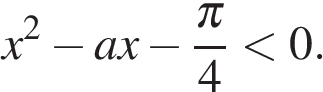
Теперь заметим, что старший коэффициент квадратного трехчлена 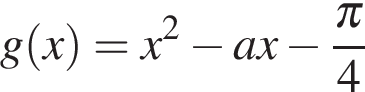 положителен, а
положителен, а 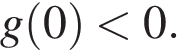 Тогда если
Тогда если  то
то 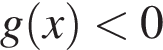 на всем отрезке
на всем отрезке 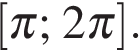 Таким образом,
Таким образом, 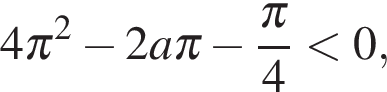 откуда
откуда 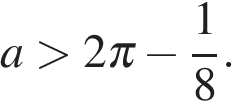
Укажем иной путь.
Пусть 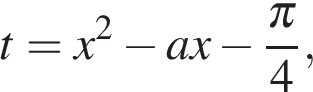 тогда
тогда 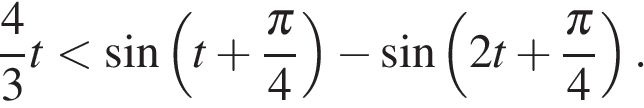 Преобразуем правую часть:
Преобразуем правую часть:
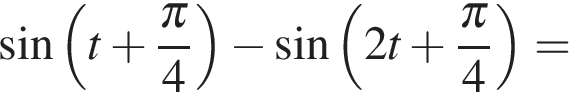
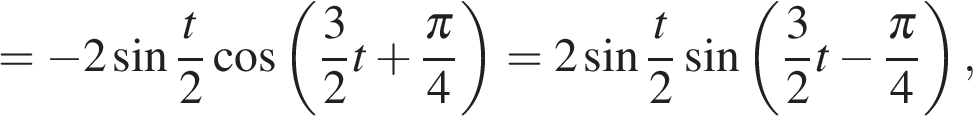
получаем
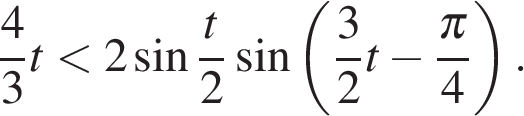
Если 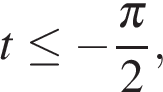 то
то 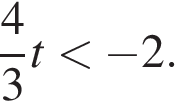 Все такие числа t являются решениями, так как правая часть не меньше −2.
Все такие числа t являются решениями, так как правая часть не меньше −2.
Если 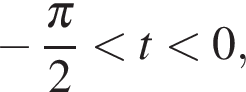 то левая часть отрицательна, а правая положительна. Неравенство верно.
то левая часть отрицательна, а правая положительна. Неравенство верно.
Если  то обе части неравенства равны 0. Неравенство неверно.
то обе части неравенства равны 0. Неравенство неверно.
Если 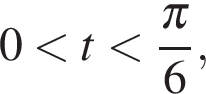 то левая часть положительна, а правая отрицательна. Решений нет.
то левая часть положительна, а правая отрицательна. Решений нет.
Если 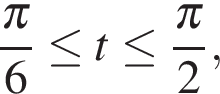 то в силу неравенства
то в силу неравенства 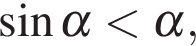 справедливого для положительных α получаем:
справедливого для положительных α получаем:
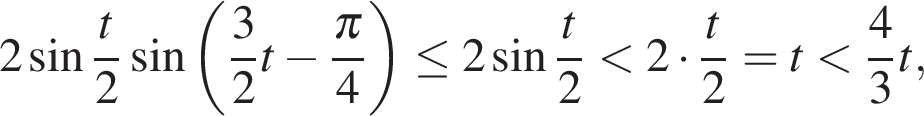
а значит, правая часть меньше левой, и неравенство не имеет решений.
Если 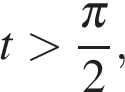 то
то 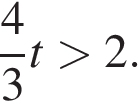 В этом случае решений нет, так как правая часть не больше 2.
В этом случае решений нет, так как правая часть не больше 2.
Тем самым искомыми являются значения  Следовательно,
Следовательно, 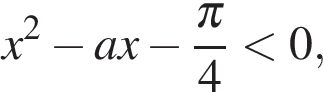 и далее как ранее.
и далее как ранее.
Задание 18 № 552515
Найдите все значения параметра а, при которых неравенство
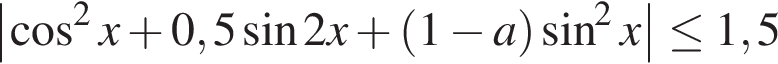
выполняется для любого действительного числа х.
Решение.
Заметим, что если 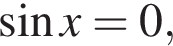 то неравенство верно при любом значении параметра a. Рассмотрим случай
то неравенство верно при любом значении параметра a. Рассмотрим случай 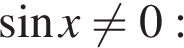
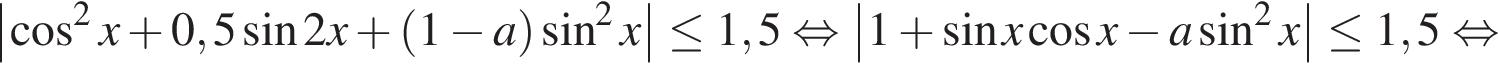
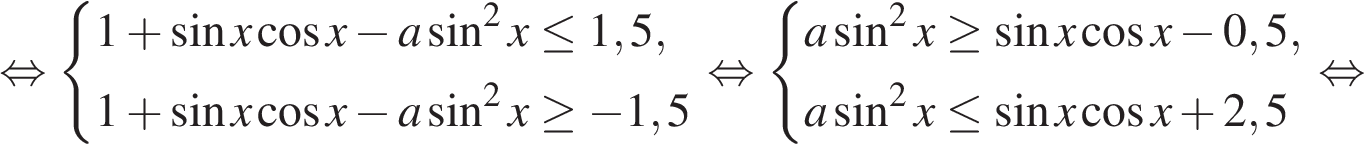
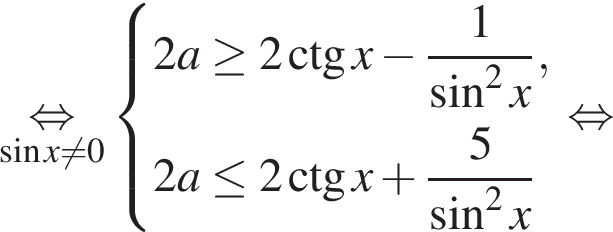
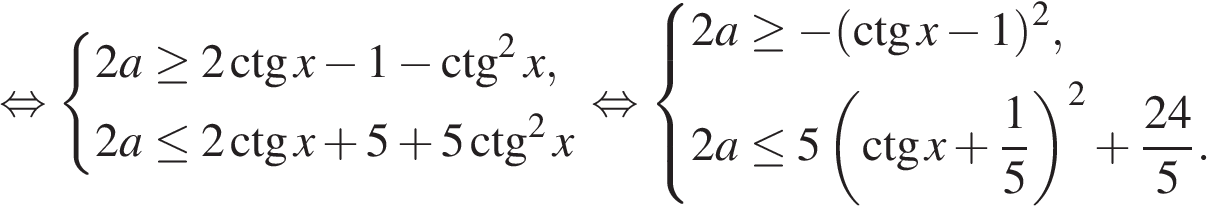
При 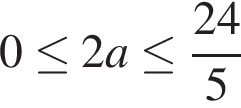 и первое, и второе неравенства системы имеют решения для любого значения переменной, удовлетворяющего условию
и первое, и второе неравенства системы имеют решения для любого значения переменной, удовлетворяющего условию 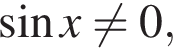 причем правая часть второго неравенства не меньше правой части первого, а потому и вся система в целом имеет решения.
причем правая часть второго неравенства не меньше правой части первого, а потому и вся система в целом имеет решения.
Таким образом, исходное неравенство выполняется для любого действительного числа х, если 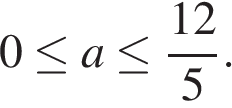
Ответ: