Для анализа динамических рядов используются различные показатели и характеристики, их принято разделять на показатели (характеристики) по уровням ряда и характеристики по ряду в целом.
К характеристикам по уровням относятся абсолютные приросты:
Базисные:
Yt – текущий уровень ряда
Y0 – базисный (начальный) уровень ряда
Цепные:
Темпы роста базисные:
Цепные:
Темпы прироста базисные:
Цепные:
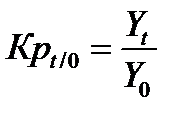
Коэффициенты роста – базисные:
Цепные:
Абсолютное содержание одного процента роста:
Таким образом содержание одного процента роста это сотая часть предшествующего уровня или базисного уровня если t = 1.
Между рассмотренными показателями имеет место соотношение:
Характеристики динамики по динамическому ряду в целом и их использование для сглаживания рядов и получения точечных прогнозных оценок.
Для анализа динамических рядов используются различные показатели и характеристики, их принято разделять на показатели (характеристики) по уровням ряда и характеристики по ряду в целом.
Показатели для ряда в целом:
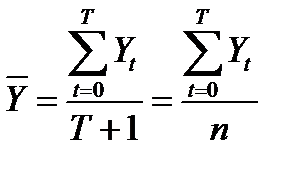Средний уровень ряда определяется для интервального ряда как простая среднеарифметическая:
Для ряда моментных показателей как средняя хронологическая:
Средний абсолютный прирост определяется:
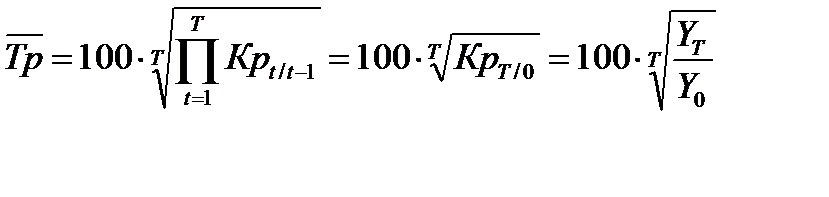Средний темп роста:
Средний абсолютный прирост и средний темп роста (коэффициент роста) могут быть использованы для получения точечных прогнозных оценок.
Сглаживание:
Используется уравнение тенденции динамики – тренд. И рассмотрим линейную форму тренда:
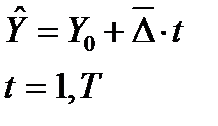
Y – уровни, освобожденные от колебаний, выровненные по прямой
|
|
Y0 – начальный уровень тренда в момент или период, принятый за начало отсчета времени t
D - среднегодовой абсолютный прирост
Прогноз на основе среднего абсолютного прироста:
l – шаг прогноза или период упреждения
L – длина прогноза
Ограничения для прогноза:
L £ T/3 (L £ T/4)
T –предыстория, L – прогноз
Прогноз на основе среднего коэффициента роста:
Используется для сглаживания тренд в форме степенной кривой
Прогноз:
Скользящее среднее
Сглаживание или механическое выравнивание динамического ряда, сводится к замене фактических уровней расчетными имеющими меньшую колеблимость. Это позволяет тенденции развития проявить себя более наглядно. Один из наиболее простых методов сглаживания заключается в расчете скользящих (подвижных) средних.
Метод скользящей средней, суть этого метода состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
Для динамического ряда Yt t = 0,1,…T определяется период сглаживания m (число уровней) обычно нечетное. m < n = T + 1
Вычислив среднюю для первых m уровней
Y0, Y1, …, Ym-1
Переходят к вычислению средней уровней
Y1, Y2, …, Ym
Затем уровней
Y2, Y3, …, Ym+1
Таким образом интервал из m уровней для которого рассчитывается среднее, как бы скользит по динамическому ряду с шагом (для интервала) равным единице.
Если m нечетное
m ³ 3 то m = 2 p + 1, p = m-1/2/
Скользящее среднее определяется как простая арифметическая средняя:
|
|
Таким образом число скользящих средних на 2p меньше числа n = T + 1, т.е. числа уровней динамического ряда.
Чем больше период сглаживания, тем в общем случае наглядней проявляется тенденция, но вместе с тем (особенно для коротких динамических рядов, может оказаться чувствительной потеря информации). Расчет скользящей средней при большом числе уровней может осуществляться по рекуррентной формуле:
При этом для первых m уровней рассчитывается скользящая средняя которая принимается в данной рекуррентной формуле за Yt-1. Таким образом последующая скользящая средняя уменьшается на одну m – ную выходящего из интервала уровня и увеличивается на одну m – ную вновь входящего в данный ряд уровня. Упрощение расчета может осуществляться также с использованием кумулятивной суммы уровней. Uj – сумма уровней от начального до j.
Кроме простых скользящих средних, используют также взвешенные скользящие средние при вычислении которых каждому уровню входящему в интервал сглаживания придаются веса, которые вычисляются из условия сглаживания симметричными кривыми с вершиной в середине интервала в виде полиномов второй, третьей степени и более высоких степеней.
Существует еще экспоненциальное среднее, в которых «веса» экспоненциально убывает по мере удаления в предысторию процесса это позволяет отражать влияние последних изменений уровней динамического ряда, что часто используется в прогнозирование.