Дифференциальное уравнение САР получим из передаточной функции по входным воздействиям САР по принципу суперпозиции: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности.
Рис.8. Структурная схема САР
Выходной сигнал САР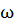 
можно определить через задающее и возмущающее воздействия следующим образом:
где 
– задающее воздействие, 
– возмущающий фактор.
Заменяем 
:
.
Проверка САР на устойчивость
По корням характеристического уравнения системы
Используя программный продукт MatLab, получим значения корней характеристического уравнения системы:
>> W=tf([0.2473],[1 4.043 4.024 1.331 1.2473])
Transfer function:
0.2473
---------------------------------------------
s^4 + 4.043 s^3 + 4.024 s^2 + 1.331 s + 1.247
>> pole(W)
ans =
-2.6440
-1.4065
0.0037 + 0.5791i
0.0037 - 0.5791i
Для того чтобы линейная система была устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения были левыми. В нашем случае корни S2,3 являются правыми, следовательно, система неустойчива.
По критерию устойчивости Михайлова
Для того, чтобы проверить САР на устойчивость критерием Михайлова, необходимо построить годограф Михайлова:
.
Перейдем в частотный диапазон, заменив 
, выделим вещественную и мнимую составляющие, получим уравнение кривой Михайлова:
.
Теперь представим D(jω) в виде:
,
где U(ω) и V(ω) - вещественная и мнимая функции Михайлова соответственно.
Построим годограф Михайлова, используя MatLab:
>> w=0:0.1:1
>> p=1*w.^4-4.024*w.^2+1.247
>> q=-4.043*w.^3+1.331*w
>> plot(p,q)
>> grid
Получили график:
Рис.9. Годограф Михайлова
Для устойчивости САУ необходимо и достаточно, чтобы кривая (годограф) Михайлова, начинаясь при 
на вещественной положительной полуоси с ростом частоты от 0 до 
, обходила последовательно в положительном направлении 
квадрантов комплексной полуоси, где n-степень – это корень характеристического уравнения.
Вывод: из графика видно, что наш годограф начинается на положительной действительной оси, движется по часовой стрелке, проходя 3 квадранта. Система устойчива.
По критерию устойчивости Найквиста
Для того чтобы САУ устойчивая и нейтральная в разомкнутом состоянии, была устойчива в замкнутом состоянии необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы не охватывал точку М(-1; j0) на комплексной плоскости при изменении частоты от 0 до ∞ и повороте вектора АФЧХ по часовой стрелке.
Замкнутая САУ устойчива, если ее АФЧХ пересекает ось частот правее места пересечения ее ЛАЧХ разомкнутой системы.
Итак, воспользуемся характеристическим уравнением разомкнутой системы:
Численный расчет произведем в MatLab:
>> num=[0.2473]
>> den=[1 4.043 4.024 1.331 1.2473]
>> w=1:0.1:30
>> APK=freqs(num,den,w)
>> u=real(APK)
>> v=imag(APK);t=0:pi/100:2*pi;
>> x=sin(t)
>> y=cos(t)
>> plot(u,v,x,y)
>> grid
Получили следующий график:
Рис.10. Годограф Найквиста
Вывод: годограф кривой Найквиста, согласно рис.10, не охватывает точку с координатой (-1; j0), значит, система устойчива.