Напряжения смятия и контактные напряжения.

Лекция 9.

Местные напряжения.

Прочность при переменных напряжениях.

ПЛАКАТ 1,2,3

Концентрация напряжений.

Рассмотренные ранее методы расчетов на прочность и жесткость исходили из принципа Сен-Венана. При этом мы рассматривали стержни постоянного сечения по длине. Эти расчеты позволяют достаточно точно определять напряжения и дают погрешности только в местах приложения нагрузок и резкого изменения размеров сечения.

Концентрация напряжений – это значительное повышение напряжений в местах резкого изменения геометрической формы стержня.

Причина, вызвавшая это явление – отверстие, выточка, надрез и т.д. – называется концентратором напряжения.

Количественной характеристикой концентрации напряжений являются коэффициенты концентрации напряжений:

Теоретический коэффициент концентрации напряжений – α_к, зависит только от вида и размеров концентратора, и равен отношению максимального местного напряжения σ_max к номинальному напряжению σ_н.

(1)

Эффективный коэффициент концентрации напряжений определяют опытным путем, как отношение предела прочности σ_в детали без концентратора к пределу прочности σ_в.к. детали с концентратором напряжений.

(2)

Значения коэффициентов приводятся в справочнике.

При статических нагрузках концентрация напряжений в деталях изготовленных из пластичных материалов, не является опасной благодаря перераспределению напряжений в зоне концентрации за счет текучести материала. При этом k_S = 1. При таких нагрузках концентрация напряжений должна учитываться при расчете деталей из хрупких или малопластичных материалов. При динамических нагрузках концентрация напряжений существенно снижает прочность деталей, как из хрупких, так и из пластичных материалов.

Рассмотрим примеры распределения напряжений в деталях с концентраторами.

ПЛАКАТ 4

Напряжения смятия и контактные напряжения.

Высокие местные напряжения возникают в местах передачи давления от одного тела к другому. Если начальный контакт тел происходит в одной точке или по линии, то напряжения называют контактными, если начальный контакт происходит по площадке конечных размеров, принято говорить о напряжениях смятия.

Контактные напряжения играют основную роль при расчете шариковых и роликовых подшипников, зубчатых колес, кулачковых механизмов и т.п. На смятие рассчитывают шпоночные, шлицевые, заклепочные соединения.

При расчете на смятие считают, что напряжение распределено равномерно по площадке контакта. С учетом данного допущения условие прочности на смятие:

(3)

где [ σ ] _см = 2…2,5 [σ]_сжат.

Если контакт осуществляется по поверхности полуцилиндра, то площадь смятия определяется А_см=d· l.

Контактные напряжения рассмотрим на примере сжатия цилиндров. Под действием сжимающих сил вследствии деформации цилиндров образуются площадки контакта. При этом в поверхностных слоях материала деталей возникают местные деформации и напряжения которые называют контактные напряжения. Силы давления по площадке контакта распределяются по эллиптическому закону. Максимальные контактные напряжения возникают в центре, они определяются по формуле Герца – условию контактной прочности:

(4)

μ = 0,3 – коэффициент Пуассона для стали.

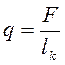- интенсивность силы давления по длине контактной линии;

- приведенный модуль упругости материалов цилиндров,

- приведенный радиус кривизны поверхностей в месте контакта.