Выполняется отдельно для целой и дробной частей данного числа. Полученные при этом целая и дробная части числа в новой системе счисления складываются.
Перевод отрицательных чисел выполняется без учета знака “минус”; знак “минус” просто дописывается к полученному числу.
Примеры (см. выше – перевод целых (стр. 12) и дробных (стр. 14) чисел):
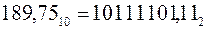[11]
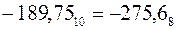
5. Перевод чисел из двоичной, восьмеричной
и шестнадцатеричной систем счисления
в десятичную систему
Перевод чисел из различных систем счисления в десятичную выполняется на основе представления этих чисел в развернутой форме (см. стр. 6) с основанием, записанным в десятичной системе, и последующим выполнением действий по правилам десятичной арифметики. Для отрицательных чисел знак “минус” удобнее учитывать только после проведения расчёта.
Примеры:
1) 
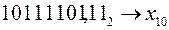
2) 
3) 
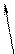
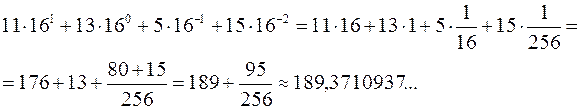
Поскольку дробная часть данного шестнадцатеричного числа не может быть представлена в десятичной системе счисления конечной дробью, определим необходимую точность. В шестнадцатеричном числе второй знак после запятой даёт точность 
. Чтобы получить точность, не меньшую, чем , в десятичной дроби следует записать три знака после запятой (точность 
). Округление проводим по правилам десятичной системы счисления.
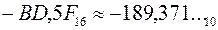
Разница между полученным результатом и исходным значением 
(см. «Перевод смешанных десятичных чисел в другие системы счисления» на стр. 20) объясняется наличием погрешности при переводе дробных чисел из одной системы счисления в другую.
6. Перевод чисел из восьмеричной системы
счисления в двоичную и обратно
Таблица 1.
Таблица соответствия (двоично-восьмеричный код):
| Х8 | У2 |
Для того чтобы перевести число из восьмеричной системы счисления в двоичную, каждую восьмеричную цифру нужно заменить триадой двоичных цифр.
Пример:
(Полученный результат подтверждает пример из раздела “Перевод смешанных десятичных чисел в другие системы счисления” на стр. 20.)
Для перевода числа из двоичной системы счисления в восьмеричную, его нужно разбить на триады вправо и влево от запятой, дополняя при этом в случае необходимости крайние левую и правую триады нулями до полных.
Пример:
[12]
7. Перевод чисел из шестнадцатеричной
системы счисления в двоичную и обратно
Таблица 2.
Соответствие для двоично-шестнадцатеричных кодов
| Х16 | У2 |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Для того чтобы перевести число из шестнадцатеричной системы счисления в двоичную, каждую шестнадцатеричную цифру нужно заменить тетрадой двоичных цифр.
Пример:
Сравните дробную часть полученного двоичного числа с результатом перевода (стр. 15) дробного десятичного числа 
в двоичную систему счисления. Разница в последнем знаке определяется округлением при переводе этого числа как в двоичную (см. стр. 15) 
, так и в шестнадцатеричную (стр. 18) 
системы счисления.
Для перевода числа из двоичной системы счисления в шестнадцатеричную, его нужно разбить на тетрады вправо и влево от запятой, дополняя при этом в случае необходимости крайние левую и правую тетрады нулями до полных.
Примеры:
1) 
(см. перевод целого десятичного числа 189 в двоичную (стр. 13) и шестнадцатеричную (стр. 13) системы счисления и дробного десятичного числа 0,75 в двоичную (стр. 14) и шестнадцатеричную (стр. 18) системы счисления).
2) 
Но с другой стороны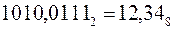 
(см. перевод чисел из двоичной системы счисления в восьмеричную на стр. 22), таким образом 
и переход от шестнадцатеричной системы счисления к восьмеричной и обратно можно осуществлять в два этапа, через двоичную систему счисления, используя двоично-восьмеричный и двоично-шестнадцатеричный код.