Вопрос 10. Кольцо многочленов от одной переменной.

Вопрос предполагает решение проблемы построения кольца многочленов как алгебры и решение проблемы о корнях многочлена.

Для построения кольца многочленов как алгебры напомним определение алгебры.

Определение 1. Алгеброй называется упорядоченное множество двух множеств , где множество элементов любой природы, а V – множество операций.

Одной из алгебр является кольцо.

Определение 2. Кольцом называется алгебра с двумя бинарными операциями – сложение и умножение -, удовлетворяющих следующим свойствам:

1. < K, +> - аддитивная абелева группа;

2. “ ´ ”- ассоциативная операция;

3. Сложение и умножение связаны дистрибутивным законом.

Для построения кольца многочленов зададим кольцо К и введем понятие многочлена.

Определение 3. Многочленом f(x) называется сумма a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀, где a_iÎK, x – неизвестное, xÏK, x⁰=1, 1·x= x. a_i называют коэффициентами многочлена, a_n - старшим, a₀ – свободным членом.

Определение 4. Суммой двух многочленов и 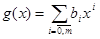называется многочлен h(x)=f(x)+g(x), h(x)=c_kx^k+...+c_{0 ,} где c_i=a_i+b_i. Определение 5. Произведением двух многочленов и называется многочлен 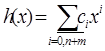, где .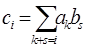

Обозначим множество всех многочленов с коэффициентами из кольца K через K[x] и рассмотрим алгебру <K[x], +, ´>. Докажем теорему о том, что эта алгебра является кольцом.

Теорема 6. Алгебра многочленов <K[x], +, ´>, с коэффициентами из кольца K образует кольцо.

g 1. f(x)+(g(x)+h(x))=(f(x)+g(x))+h(x)

f(x)+g(x)=g(x)+f(x)

f(x)(g(x)h(x))=(f(x)g(x))h(x)

f(x)(g(x)+h(x))=f(x)g(x)+f(x)h(x)

Ассоциативность сложения и умножения, коммутативность сложения и дистрибутивные законы непосредственно вытекают из введенных нами операций над многочленами.

2. - называют нулевым многочленом, легко проверить, что , т.е. - выполняет роль нулевого элемента в алгебре K[x].

3. f(x)=(-a_n)xⁿ+...+(-a₁)x+(-a₀)=-f(x) – называют противоположным многочленом для многочлена f(x), он выполняет роль противоположного элемента в алгебре. Так как все аксиомы кольца выполняются, то <K[x],+,´> - кольцо, которое обозначают K[x] и называют кольцом многочленов над кольцом K.

Теорема 7. Если K область целостности, то K[x] тоже область целостности.

Для доказательства этой теоремы введем понятие степени многочлена.

Степенью многочлена f(x) называется максимальный показатель степени x с коэффициентом отличным от нуля. Обозначение: deg f(x)=n, где a_n¹0.

Степень многочлена обладает свойствами:

deg (f + g) £ max (deg f, deg g); deg (fg) = deg f + deg g, если K – область целостности. Доказательство свойств степени многочлена осуществляется на основе двух аргументов: во-первых, на основании выполнения операций; во-вторых, на основании целостности K.

Приступим к доказательству теоремы. Требуется проверить выполнимость: (1) коммутативности умножения и (2) отсутствие делителей нуля.

(1) коммутативность умножения следует из определения умножения многочленов над областью целостности, где умножение элементов коммутативно.

(2) f(x)¹ , deg f(x)=n³0, g(x)¹ , deg g(x)=m³0,

deg (f(x)g(x))=deg f(x)+deg g(x)= n+m ³0 Þ deg (fg) = n+m ³ 0 Þ $ c_n+m ¹ 0 Þ (fg)¹ , это и доказывает отсутствие делителей нуля в K[x], где K – область целостности.

Пусть возникла ситуация, где требуется многочлен f(x) = a_nxⁿ+...+a₁x+a₀ разделить на двучлен (x-a). Это можно сделать с помощью алгоритма, который принято в математике называть схемой Горнера. Построим этот алгоритм.

f(x) = (x-a)g(x)+r(x), где f(x) = a_nxⁿ+...+a₁x+a₀, g(x)= b_nxⁿ+...+b₁x+b₀ .

Воспользуемся свойством степени, получим:

deg f(x) £ deg [(x-a)g(x)+r(x)]£ max[deg (x-a)g(x), deg r(x)]

deg (x-a)g(x)=deg (x-a)+deg g(x). Из этих равенств можно сделать вывод, что m=n-1, deg r(x)=0, т.е. r(x) – число, т.е. a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀=(x- -a)b_nxⁿ+...+b₁x+b₀+r. Раскроем скобки справа и приравняем коэффициенты многочленов. Для удобства одновременно воспользуемся схемой.

a_nxⁿ=b_n-1xⁿ Þ b_n-1=a_n

a_n-1x^n-1=b_n-1xⁿ(-a)+b_n-2x^n-1 Þ a_n-1=b_n-1(-a)+b_n-2 Þ b_n-2=a_n-1+ab_n-1

b₁=ab₂+a₂, b₀=ab₁+a, r=ab₀+a₀.

Введем понятие корня многочлена.

Определение 8. Число x=a называется корнем многочлена f(x), если значение многочлена f(a) равно нулю.

Рассмотрим теорему Безу о делении многочлена на двучлен (x-a).

Теорема 9. (Безу) Остаток от деления многочлена f(x) на двучлен (x-a) равен f(a).

g f(x), (x-a). Поделим, f(x)=(x-a)g(x)+r, мы установили, что r – число. Подставим x=a в равенство, получим f(a)=0g(a)+r, откуда вытекает утверждение теоремы f(a) = r.

Из теоремы вытекает следствие: f(x)M(x-a) Û x=a корень уравнения.

Þ f(x) M (x-a) Þ f(x)=(x-a)g(x)+f(a) (по теореме Безу), f(a)=0 Þ x=a корень f(x)

Ü Пусть x=a корень многочлена, т.е. f(a)=0 Þ f(x)=(x-a)g(x) (по теореме Безу), т.е. f(x) M (x-a).