Вопрос 11. Кольцо многочленов над полем комплексных чисел.

В алгебре многочленов имеют место две взаимно пересекающиеся, взаимно дополняющие линии. Это вопросы существования и количества корней многочлена и разложение многочлена на неприводимые множители.

В вопросе представлено решение этих аспектов для кольца многочленов над полем комплексных чисел, т.е. для кольца C[x], где C – поле комплексных чисел.

Итак, пусть P – поле.

Определение 1. Поле P называется алгебраически замкнутым, если любой многочлен положительной степени имеет в этом поле корень. Алгебраической замкнутостью обладает поле C, это решается основной теоремой алгебры.

Теорема 2. Любой многочлен положительной степени из кольца C[x] обладает по крайней мере одним корнем. Примем эту теорему без доказательства в силу того, что она требует предварительного доказательства ряда теорем из математического анализа.

Из основной теоремы алгебры вытекает ряд следствий, их и рассмотрим.

Следствие 3. Неприводимым над полем C многочленом является многочлен только первой степени.

Для доказательства этого утверждения введем определения приводимого и неприводимого многочлена. Многочлен f(x)ÎP[x] называется приводимым, если его можно представить в виде произведения двух многочленов меньшей положительной степени. В противном случае многочлен называется неприводимым.

Приступим к доказательству следствия 3.

Пусть дан f(x)ÎC[x]. Пусть он приводим. Покажем, что

1. рассмотрим f(x)=a₁x+a₀, degf(x)=1. Предположим, что f(x) – приводим. Тогда по определению приводимого многочлена f(x)=f₁(x)f₂(x), где degf₁(x)>0, degf₂(x)>0. Однако по условию degf(x)=1=1+0=0+1, то есть degf₁(x)=0Èdegf₂(x)=0, что противоречит свойству степеней. Полученное противоречие и доказывает неприводимость многочлена (а₁х+а₀).

Пусть deg f(x)>1, тогда по основной теореме алгебры он обладает корнем. Пусть таким корнем будет х=а. По следствию из теоремы Безу: f(x)=(x-a)f₁(x). Так как deg(x-a)=1, degf(x)>1, deg(x-a)f₁(x)=deg(x-a)+degf₁(x), то degf(x)>0; то есть f(x) – приводим, что противоречит условию. Таким образом, неприводимым над полем С является только многочлен первой степени.

Следствие 4. Если f(x)ÎC[x], degf(x)=n³1, то его можно представить в виде:

с(x-a₁)(x-a₂)...(x-a_n), (*)

где a_i – корни его, а сÎС.

g Пусть f(x)=c₁x+c₀=c₁ 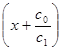=c₁(x-a₁), где 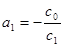, то есть для многочлена f(x) утверждение верно: он представляется в виде (*) и а₁ – корень его, а с₁ – старший коэффициент.

Далее, проведем доказательство методом математической индукции. Пусть теорема верна для многочлена степени меньшей или равной (n-1), то есть

f(x)=c(x-a₁)...(x-a_n-1), где a₁, a₂,..., a_n-1 – его корни, а с – старший коэффициент.

Пусть f(x) – неприводим, а это возможно только для n=1, для этого случая теорема верна. Либо f(x) – приводим, тогда f(x)=g(x)h(x), где степени g(x) и h(x) меньше n, для них теорема верна. В силу свойства степени f(x)=c(x-a₁)...(x-a_n), то есть множителей будет ровно n. По следствию из теоремы Безу а_i – корни f(x), если расткрыть скобки в правой части и воспользоваться равенством многочленов, то с – старший коэффициент f(x). Теорема доказана.

Из этого в следствии с необходимостью вытекает еще два.

Следствие 5. Количество комплексных коней многочлена f(x)ÎC[x] совпадает с его степенью.

Следствие 6. Любой многочлен f(x)ÎC[x] положительной степени n можно представить в виде:

f(x)=c(x-a₁)^a₁(x-a₂)^a₂...(x-a_k)^a_k, где a₁+...+a_k=n, a_i – его корни. Такое представление носит название канонического. Возможность такого представления вытекает из следствия (4) и допустимости повторяющихся корней, то есть кратных корней многочлена.

В теории многочленов над С имеет место теорема, устанавливающая связь между корнями многочлена и его коэффициентами.

Теорема 7. Пусть f(x)ÎC[x], degf(x)=n, a_n=1 (то есть f(x) – нормирован), тогда как известно, f(x)=(x-a₁)(x-a₂)...(x-a_n), где имеет место соотношение:

а₀ = (-1)ⁿ a₁ a₂ ... a_n;

a¹= (-1)^n-1 (a₁a₂ ... a_n-1+... + a₂a₃... a_n);

.........

a^n-2= a₁a₂+ a₁a₃+... + a_n-1a_n ;

a^n-1= -(a₁+ a₂+... +a_n);

эти соотношения называются формулами Виета. Однако, справедливости ради, надо отметить, что Виет нашел эту зависимость только для случая положительных корней, в общем виде эта теорема установлена А. Жирарое.

 

Вопрос 12 Кольцо многочленов над полем действительных чисел (R).

В алгебре имеет место теория многочленов. Многочлен введен по определению как выражение f(x)=a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀, где a_iÎK – кольцо, x⁰=1, 1·x= x. Введение операций “+” и “´” многочленов позволило построить алгебру многочленов, которой является кольцо многочленов над кольцом К и обозначается К[x]. Особый интерес представляет теория многочленов, когда вместо кольца К взято поле. Такими числовыми полями являются C, R, Q.

В силу существования операции деления в поле, стало возможным рассматривать два взаимосвязанных вопроса в теории многочленов: корни многочлена и разложение многочлена на неприводимые многочлены.

Рассмотрим решение этой проблемы для кольца многочленов над R.

Теорема 1. Комплексные корни f(x)ÎК[x], то есть с действительными коэффициентами попарно сопряженными.

n Пусть f(x)ÎК[x], и пусть z=a+bi; a,bÎR комплексное число, являющееся корнем f(x), причем degf(x) ³2 в противном случае f(x) комплексных корней иметь не может. Покажем, что 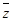= a–bi, b¹0 тоже является корнем f(x).

f( 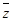)=a_n 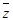ⁿ+a_n-1 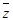^n-1+...+a₁ 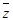+a₀= (воспользуемся свойством сопряжения) = = 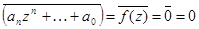, то есть 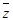является корнем f(x), что и требовалось доказать.

Рассмотренная выше теорема позволяет доказать теорему о неприводимом многочлене из R[x]. Напомним определение приводимого и неприводимого многочленов.

f(x) называется неприводимым, если его можно представить в виде произведения двух многочленов меньшей положительной степени и неприводимым, если этого сделать нельзя.

Рассмотрим f(x)= a₁x+a₀, a_iÎR. его нельзя представить в виде произведения двух многочленов меньшей положительной степени в силу того, что 1=1+0=0+1.

Решать будем вопрос о приводимости и неприводимости многочлена f(x)ÎR[x] степени большей или равной 2.

Теорема 2. Неприводимый многочлен f(x)ÎR[x], degf(x)=n³2 ассоциирован с многочленами (x-a)²+b²,где x=a+bi комплексный его корень.

n Пусть f(x)ÎR[x], degf(x)=n³2, пусть x=a+bi, b¹0 – корень f(x), он неприводим.

Прежде всего отметим, что у такого многочлена нет действительных корней, иначе бы f(x)=(x-a) f₁(x) (следствие из теоремы Безу), что противоречило бы его неприводимости.

По теореме о сопряженности мнимых корней многочлена с действительными коэффициентами f(x) обладает еще одним корнем x₂=a–bi, где x₂= .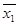

Рассмотрим (x-x₁)(x-x₂)=(x-a)²+b². (*)

Разделим f(x) на многочлен (*), получим:

(1) f(x)=[(x-a)²+b²]g(x)+r(x).

Так как степень делителя равна 2, то degr(x)<2, то есть r(x)=cx+d. Подставим в (1) x1=a=bi и x₂=a-bi, мы получим: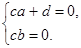

Так как b¹0, то c=0, тогда d=0, то есть r(x)= .

Это означает, что f(x)M (*). Но f(x) – неприводим, потом deg g(x)=0, то есть g(x)ÎR. Что и подтверждает ассоциированность f(x) и (*).

Теорема 3. Рассмотренная выше теорема позволит сделать ряд выводов:

1. Неприводимыми многочленами над R могут быть многочлены не выше второй степени.

2. Многочлен f(x)ÎR[x], degf(x)³1 может быть представлен в ви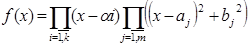де:

, где 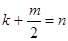если среди корней есть кратные, то можно представить и в виде (*):

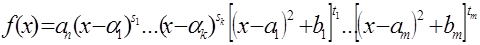, где S_i – кратности корней, а t_j – кратности сопряженных мнимых его корней. Представление (*) называется каноническим представлением f(x).

Теорема 4. Теоремы (1), (3) позволяют сделать с очевидностью вывод о том, что четность действительных корней совпадает с четностью его степени.

Вопрос 13.Кольцо многочленов над полем рациональных чисел (Q).

Теория многочленов утверждает, что множество многочленов f(x) = a_n xⁿ + …+ a₁ x + a₀,

где a_i ∈ K – кольцо, x⁰=1, x∈K, 1∙x=x с операциями сложения и умножения образуют кольцо многочленов над кольцом K и обозначают K [ x ].

Особый интерес представляет теория многочленов, когда вместо кольца K рассматривается поле P. В силу того, что в поле P есть операция деления, становится возможным построить теорию корня многочленов и теорию приводимых и неприводимых многочленов. Рассмотрим, как решается эта проблема в Q [ x ].

Напомним, что корнем f(x) называется такое число x = a, что f(a) = 0.

f(x) называется неприводимым, если его нельзя представить в виде двух многочленов меньшей положительной степени, в противном случае его называют приводимым.

Итак, пусть Q [ x ], f(x)∈ Q [ x ], где f(x) = a_n xⁿ + …+ a₁ x + a₀ …(1), сформулируем и докажем теорему о рациональных корнях многочлена с целыми коэффициентами. Если многочлен имеет рациональные коэффициенты, то он легко преобразуется к ему ассоциированному с целыми коэффициентами. Поэтому теорию существования и нахождения корней f(x)∈ Q [ x ] рассматривают именно для такого варианта, т.е. f(x)∈ Q [ x ], а a_i ∈ Z.

Теорема 1: Если 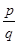∈Q, где (p,q)=1, является корнем многочлена (1)… f(x) = a_n xⁿ + …+ + a₁ x + a₀, a_i ∈ Z, то p является делителем свободного члена, а q -делителем старшего коэффициента a_n.

■ Если 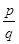∈Q корень f(x), то f 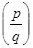=0. Подставим в (1) 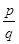вместо x, получим

0= a_n + …+ a₁ 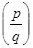+ a₀, приведём к общему знаменателю, получим

0= a_n pⁿ + a_n-1 p^n-1 q+…+ a₁ p q^n-1 + a₀ qⁿ …(2).

Преобразуем (2):

2.1: 0 = a_n pⁿ + q(a_n-1 p^n-1 +…+ a₁ p q^n-2 + a₀ q^n-1) ⇒ a_n pⁿ + q Q ∶ q, qQ ∶ q

⇒ a_n pⁿ ∶ q, (p,q)′→ a_n ∶ q, т.е. q- делитель старшего коэффициента;

2.2: 0 = p(a_n p^n-1 +…+ a₁ q^n-1 ) + a₀ qⁿ) ⇒ pQ + a₀ qⁿ ∶ p, pQ ∶ p, ⇒ a₀ qⁿ ∶ p, (q,p)=1 ⇒ a₀ ∶ p, т.е. p -делитель свободного члена, что и доказывает теорему.

Следствие 2: Если f(x)∈ Q [ x ], а a_i ∈Z, a_n= 1, то он обладает только целыми корнями, которые находятся среди делителей свободного члена.

Истинность этого утверждения очевидна в силу того, что a_n= 1, а делители 1 являются только ±1, следовательно, q= ±1 и 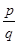∈Z. Т.к. 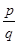= ± p∈Z находятся среди делителей, то утверждение верно.

Решим проблему неприводимости многочлена из Q [ x ], вернее о степени такого многочлена.

Решение этой проблемы предложено Эйзенштейном и носит название критерий Эйзенштейна о неприводимости многочлена в Q [ x ]. Заметим, что решение этой проблемы тоже есть смысл рассматривать для f(x)∈ Z [ x ], поскольку Q является полем частных области целостности Z.

Теорема 3: Пусть f(x)= c_n xⁿ + …+ c₁ x + c₀, c_i ∈Z. Пусть все коэффициенты f(x), кроме старшего, делятся на p². Тогда f(x) неприводим в Z [ x ].

■ Доказательство проведём методом от противного.

Пусть f(x)∈ Q [ x ] или f(x)∈ Z [ x ] приводим, т.е. существуют такие g(x), h(x)∈ Z [ x ], что

f(x) = (a₀ +…+a_k x^k )(b₀ +…+ b_m x^m) = g(x)·h(x), (a_k ≠ 0, b_m ≠ 0, k + m = n, причем 1≤ k, m < n).

Тогда c₀ = a₀·b₀, c_n = a_k·b_m. Так как c₀ ∶ p, c₀ не∶ p₂, c₀ = a₀·b₀ ⇒ a₀ не∶ p Λ b₀ не∶ p; пусть a₀ ∶ p,

b₀ не∶ p. Так как c_n не∶ p, то a_k не∶ p, b_m не∶ p, тогда у g(x) есть коэффициент делящийся на p и неделящийся на p. Пусть a_s коэффициент g(x) с наименьшим s таким, что a_s не∶ p, т.е. a₀, a₁, …, a_s-1 ∶ p, а a_s не∶ p.

Найдем c_s = a_s b_s + (a_s-1 b₁ + a₀ b_s) (s<n), т.к. a_s не∶ p, b₀ не∶ p, то a_s b₀ не∶ p, число (a_s-1 b₁ + a₀b_s) ∶ p, по свойству делимости в кольце Z, c_s не∶ p, s<n, а это противоречит условию. Получено противоречие в силу предположения, что f(x) - приводим. Что и доказывает теорему о неприводимости f(x).

Следствие 4: Если p – простое число и n – любое целое положительное число, то многочлен xⁿ-p неприводим в Q [ x ].

Теорема 3 и следствие 4 позволяют сделать вывод о том, что в Q [ x ] существуют неприводимые многочлены любой степени. Поэтому решение проблемы нахождения корней f(x) и разложения его на неприводимые многочлены затрудненно и требует в каждом конкретном случае особого подхода.

 

Вопрос 14. Простое алгебраическое расширение поля.

Пусть дано поле P. P[x] - кольцо многочленов от одной переменной над полем P. Обратимся к понятию алгебраической замкнутости поля P. Напомним, что поле Р называется алгебраически замкнутым, если любой многочлен f(x)ÎP[x] обладает хлтя бы одним корнем. Введем такое понятие: элемент aÎР называется алгебраическим над полем Р, если существует f(x)ÎP[x], для которого a является корнем.

Пусть дано поле Р и aÏР, aÎF – поле.

Определение 1. Простым расширением поля Р с помощью элемента a называется наименьшее подмножество поля F, содержащее Р и a. Простое расширение поля Р с помощью aÎF обозначается Р(a).

В вопросе решается проблема о строении Р(a) и возможности применения этой теории для освобождения знаменателя дроби от алгебраической иррациональности. Для решения обозначенной проблемы рассмотрим Р[a]={f(a)/f(x)ÎP[x]}, где Р[a]={a₀+a₁a+...+a_naⁿ/a_iÎP, nÎN}.

Легко проверить, что Р[a] подкольцо поля Р(a).

Теорема 2. Пусть Р[x] – кольцо над Р, Р(a) – простое расширение Р с помощью элемента a. Пусть y: Р[х] на Р[a] – отображение такое, что y(f(x))=f(a). Тогда:

1⁰. " aÎP, y(a)=a;

2⁰. y(x)=a;

3⁰. y – гомоморфизм и эпиморфизм;

4⁰. Ker y ={f(x)Î Р[x]/ f(a)=0Î Р[a]};

5⁰. Фактор-кольцо Р[х]/Ker y изоморфно кольцу Р[a].

n 1⁰ и 2⁰ следуют из определения y.

3⁰: y(f(x)+g(x))= f(a)+g(a), y(fg)=f(a)g(a), y(1)=1, это проверяется непосредственно, поэтому y – гомоморфизм; " f(a)ÎР[a], $ f(x)Î Р[x], y(f(x))=f(a) Þ y – эпиморфизм.

4⁰: следует из существования Ker f для гомоморфизма и из определения y.

Рассмотрим 5⁰. Так как Ker y – идеал Р[х], то становится возможным Р[х] факторизовать, получить Р[х]/Ker y, тогда по основной теореме об эпиморфизме колец Р[х]/Ker y º Р[a].

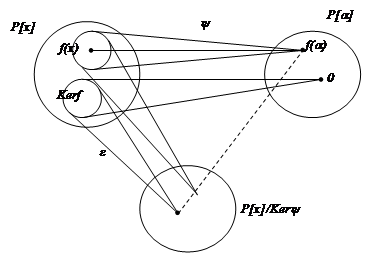
e: Р[x]® Р[x]/Kery, e (f(x))=Kf(x).

j: Р[x]/Kery® Р[a], где

j(Kf(x))=f(a)Þ j – изоморфизм.

 

Следствие 3. Если a - трансцендентный элемент над полем Р, то Р[х]@ Р[a].

n В силу трансцендентности a над Р, Kery={0} и Р[x]/{0}@ Р[a], кроме того e – изоморфизм, то есть Р[x]/{0}@ Р[x] следовательно, Р[x]@ Р[a].

Определение 4. Пусть Р[х] – кольцо многочленов над полем Р. Пусть a – алгебраический элемент над полем Р. Минимальным многочленом * a над Р называется нормированный многочлен наименьшей степени, для которого a является корнем.

Обозначим минимальный многочлен для a над Р через g(x), deg g(x)=n называют степенью алгебраического элемента a над Р.

Легко показать:

1) g(x) существует для каждого алгебраического элемента;

2) g(х) – неприводимый многочлен в Р[х] над Р;

3) g(x) для a определяется однозначно.

(1) – вытекает из определения алгебраического элемента.

(2) – из определения минимальности g(x).

(3) – из предположения, что существует два многочлена * g и h и их неприводимости, они ассоциированы, а так как они неприводимы, то g(x)=h(x).

Теорема 5. Пусть a алгебраический элемент степени n над Р (aÏ Р) и g(x) – его минимальный многочлен степени n, тогда имеют место:

1⁰. Если f(a)=0, где f(x)Î Р[х], то f(x)M g(x);

2⁰. Р[х]/(g(f))@ Р[х];

3⁰. Р[х]/(g(f)) – поле;

4⁰. Р[a]=Р(a).

n Пусть a корень f(x), то есть f(a)=0, известно, что g(a)=0, тогда (f,g) либо 1,либо нет. Первое невозможно, так как по известной теореме f(x)M (x-a) и

g(x)M(x-a). Следовательно, (f,g)¹1, то есть они не являются взаимно простыми, поэтому f(x) делится на g(x).

Зададим гомоморфизм y: Р[х]® Р[a], y(f(x))=f(a)ÞKer y={f(x),f(a)=0} состоит из многочленов, делящихся на g(x), поэтому Ker y=J=(g(x)) – идеал Р[х]Þ Р[х]/(g(x)) @ Р[a] (*), так как Р[a]ÌР(a), то Р[a] – область целостностиÞ Р[х]/(g(x)) в силу (*) тоже область целостности. Покажем, что любой элемент из Р[х]/(g(x)) ненулевой обратимый.

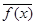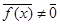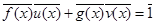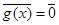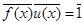Пусть смежный класс, , то f(a)=0, тогда f(x) не делится на g(x) Þ(f(x),g(x))=1Þ , но Þ Þ 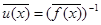, что и требовалось доказать, то есть Р[х]/(g(x)) – поле, а так как эта алгебра изоморфна Р[a], то Р[a] тоже поле являющееся подполем поля Р(a). Но Р(a) минимальное подполе поля F, следовательно, Р(a) Ì Р[a], откуда получаем, что Р[a]=Р(a).

Эта теорема позволяет установить строение простого алгебраического расширения Р(a).

Пусть a - алгебраический элемент над P, а Р(a) – простое алгебраическое расширение P, пусть степень a равна n>0. Тогда

Теорема 6. Любой элемент поля Р(a) однозначно представим в виде линейной комбинации n элементов 1,a,...,a^n-1 с коэффициентами из P.

4)

 

 

Вопрос 15. Простые и составные числа.

 

Рассмотрим N – натуральные числа. Введем понятие простого и составного числа.

Опр.1 N ' а называется делящимся на число вÎN, в > 0, если существует такое число с, что а = вс, при этом а – делимое, в – делитель, с – частное.

Все натуральные числа, в связи с отношениеми делимости на, разбиваются на группы: {0}, {1}, {р₁, р₂,…,…}, {а₁, а₂,…}, где 1 обладает только один делитель, р_i – двумя, а для а_i существует более двух.

Опр.2 Натуральное число р называется простым, если оно имеет ровно два различных делителей. (1 и само число р), составным, если имеет более двух делителей.

Введенное определение позволит выражать числа натуральные через простые. Это описывается теоремой, которую называют основной теоремой арифметики.

Теорема. 3 Любое n Î N, n > 1 можно единственным образом представить в виде произведения простых чисел с точностью до перестановки сомножителя.

В теореме содержится две теоремы: о существовании разложения и его единственности.

(7) Пусть n Î N, n > 1. Для доказательства исследуем метод математической индукции.

n = 2, 2 – простое число, следовательно n = 2 и есть его разложение.

Предположим, что для любого натурального числа, меньшего n, теорема верна и докажем для n.

Пусть дано натурально n, если оно простое, то это и есть его разложение. Если n составное, тогда n = вс, где в,с Î N и меньше n. По предположению индукции разложение их на простые множители существует, поэтому оно существует и для n. На основании принципа математической индукции, можно утверждать истенность теоремы для любого n Î N, n > 1.

(!) Докажем единственность разложения на простые множетели методом математической индукции.

n = 2, 2 = 2. Разложение единственное.

Допустим, что для любого числа натурального, меньшего n утверждение справедливо и докажем для n. Если n простое число, то это и есть его разложение и оно единственно. Если n составное, то оно допустит разложение на простые числа. Предположим, что таких разложений оказалось два: n = p₁p₂ ^¼ p_к = q₁q₂ ^… q_s (1). Из равенства (1) видно, что “правая часть” делится на p₁. А т.к. в “правой части числа простые”, то

1) существует число q_i, которое делится на p₁;

2) (p₁, q_i) = 1. Следовательно, p₁ = q_i. Пусть q_i = q₁, разделим обе части равенства (1) на p₁, получим, что и “левая часть” и “правая часть” числа натуральные, меньше n, а для них разложение единственное с точночтью до перестановки сомножителя. Поэтому при соответственно мы получаем, что n = p₁p₂ ^¼ p_к – разложение n и это разбиение единственное. Что и требовалось доказать.

Если среди простых множителей окажутся равные, то их объединяют в степень и получают представление n Î N в виде: 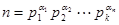, которое называют каноническим разложением натурального числа.

В теории натуральных чисел имеет место теорема, решающая вопрос о количестве простых чисел во множестве N.

Теорема 4. (Евклида) Множество простых чисел в N бесконечно.

Проведем доказательство методо от противного.

Пусть простых чисел конечное число: p₁p₂ ^¼ p_к. Рассмотрим N = p₁p₂ ^¼ p_к+1. Исследуем полученное число:

1) N > 1 => оно простое или составное; N ¹ p_i, i = 1, к;

2) N 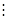p_i,, i = 1, к =>, т.к. при делении на p_i получен остаток 1;

3) N – составное. Если N составное, то ему надлежит делиться на 1, N и еще на какое-нибуть простое число (см. ниже), но это не так, поэтому N не является составным. Полученное противоречие и доказывает теорему.

Теорема 5. Наименьший, отличный от 1 делитель составного числа, является простым числом.

Пусть n Î N имеет делители, отличные от 1. Обозначим тот делитель, который будет наименьшим среди всех делителей. Пусть это натуральное число к, т.е. n = к ^. m; к, m Î N, к > 1. Исследуем к.

Если к = p – простое число, то теорема верна.

Если к – составное число, то к = к₁ m₁, тогда n = к₁ (m₁ m), n 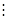к₁, к₁ < к, что противоречит выбранному наименьшему значению. Это и доказывает теорему.

 

Достаточно часто в математике приходитс для числа а Î N выяснять, является оно простым или составным. Для решения подобных задач предложен способ, носящий название “решето Эратосфена…” или способа отсеивания чисел кратных 2,3,…,p,….

Опишем этот способ.

Если даны числа натурального ряда: 1,2,3,4,5,…,n, то для установления какими они являются: простыми или составными, поступают так: вычеркивают 1,2 и каждое второе, ибо каждое второе начинается от 3, делится на 2, поэтому является составным. Затем повторяем эту процедуру для 3. 3 вычеркивается и каждое третье, ибо 6 – третье по счету за 3, делится на 3. названную процедуру повторяют до простого числа с не превосходящего 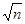. Оставшиеся числа являются простыми.

Такой алгоритм можно использовать и для установления чисел в промежутке от n₁ до n₂.

Опишем его спецификацию. Если надо установить какие числа в промежутке от n₁ до n₂ являются простыми, то поступим так:

1) выясним простое или составное является число n₁:

1.1 Проверим его делимость на 2,3,5,…p ≤ 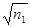. Если оно не делится на эти простые числа, то оно простое;

1.2 Если оно делится хотя бы на одно из этих чисел, то оно составное.

2) при выяснении простого числа n, одновременно поступаем так:

2.1 если n₁ 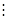2, то вычеркивают его и каждый второй (как в первом случае); и переходим к (n₁ + 1);

2.2 если n₁ 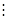2, то к числу добавляем 1 и вычеркиваем n₁ + 1 и любое второе за ним;

2.3 если было 2.1, то переходим к (n₁ + 1) и проверяется делим его на 3, повторяем процедуру решета Эратосфена переходит к (n₁ + 2);

2.4 Если было 2.2, то проверяют делимость на 3;

2.4.1. если n₁ 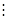3, то проверяю решето Эратосфена и переходят следующему.

не вычеркнутому числу и исследуют его делимое на 5;

2.4.2. если n₁ = 3q + r, то в зависимости от r = 1 или r = 2, добавляем 1 или 2 и

n₁ + 1, n₁ + 2.

И любое третье по счету и т.д.

2.5 Если n₁ оказалось простым, то все не вычеркнутые числа тоже простые. Если n₁ оказалось составным, а n_i – простое, то все стоящие за n_i числа остальные простые.

 

 

 

[СС1]

[D2]