Производство с двумя переменными факторами.

Изокванта.

В долгосрочном периоде все факторы производства могут быть переменными. Предположим, что процесс производства осуществляется путем использования двух факторов: капитала и труда (при таком допуще­нии мы можем использовать для анализа двухмерное графическое пространство). Соответственно существу­ет двухфакторная производственная функция, харак­теризующая зависимость между затратами труда и капитала и максимальным объемом выпускаемой продукции. Так как оба фактора — переменные, то производство одного и того же объема продукции мо­жет осуществляться путем использования их различ­ных комбинаций.

Q = f(K,L),

где К – капитал, L – труд.

При бесконечном увеличении количества производственных процессов дискретная производственная функция превращается в непрерывную функцию.

В качестве одной из первых для статистической оценки производственного процесса была использована производственная функция «Кобба-Дугласа». В самом общем виде она записывается следующим образом:

где A, а и b; – параметры, определяемые статистически; причем а + b = 1.

Функции предельной производительности являются первыми частными производными относительно труда и капитала:

Если а и b положительны, предельный продукт также должен быть положителен. Если а < 1 и b < 1, то предельные продукты труда и капитала убывают, что отражает уменьшение отдачи.

При заданной технологии один и тот же выпуск продукции может быть обеспечен с большим применением капитала или с большим привлечением труда. Возможны и промежуточные варианты. Если мы соединим все сочетания ресурсов, использо­вание которых обеспечивает одинаковый объем выпуска продук­ции, то получатся изокванты. Если изокванта является непрерыв­ной линией, то число возможных комбинаций ресурсов будет бес­конечным, что обеспечивает чрезвычайную гибкость принимаемых фирмой решений по организации

производства продукции

Рис. 4.3. Изокванты.

Изокванта, или кривая постоянного (равного) продукта, — кривая, представляющая бесконечное множество комби­наций факторов производства (ресурсов), обеспечивающих одина­ковый выпуск продукции (рис. 4.3)Изокванты для процесса производства оз­начают то же, что и кривые безразличия для процесса потребления. Они обладают аналогичными свойствами: имеют отрицательный на­клон, выпуклы относительно начала координат и не пересекаются друг с другом. Изокванта, лежащая выше и правее другой, пред­ставляет собой больший объем выпускаемой продукции. Однако, в отличие от кривых безразличия, где суммарное удовлетворение потребителя точно измерить нельзя, изокванты показывают реальные уровни производства: 10 тыс., 20 тыс., 30 тыс. и т.д.

Совокупность изоквант, каждая из которых показывает максимальный выпуск продукции, достигаемый при использовании определенных сочетаний ресур­сов, называется картой изоквант.

Изокванта не только показывает, что факторы производства взаимозаменяемы, но и дает возмож­ность определить границы субституции. Эти границы определяет предельная норма технологического заме­щения. Рассмотрим единичную изокванту (рис. 4.4). Будем двигаться по изокванте сверху вниз, замещая капитал трудом.

Если ∆К— сокращение затрат капитала, a ∆L— прирост затрат труда, то количество фактора К, кото­рое может быть замещено одной единицей фактора L,записывается как .Это предельная норма техно­логического замещения

Рис. 4.4. Предельная норма технологического замещения.

Вогнутая форма изокванты показывает, что MRTS_LKуменьшается по мере движения по изокванте сверху вниз. Это означает, что труд и капитал не являются абсолютно взаимозаменяемыми, в связи с чем возни­кают определенные трудности при замене капитала трудом, т.е. существуют определенные границы взаи­мозаменяемости факторов. Они определяются эффек­тивностью использования факторов. По мере замеще­ния в процессе производства капитала все большим количеством труда производительность труда снижа­ется и, наоборот, при замещении труда все большим количеством капитала эффективность использования капитала уменьшается. В процессе производства соче­тание факторов должно быть оптимальным.

Предельную норму технологического замещения можно рассчитать и другим способом. При движении по изокванте сверху вниз затраты капитала сокраща­ются на ΔΚ. Тогда потери производства от сокращения затрат капитала будут равны произведению ∆К на пре­дельный продукт капитала ΜΡ_К. Для того чтобы про­извести прежний объем продукции, необходимо уве­личить затраты труда на ∆L. В этом случае прирост производства, полученный за счет увеличения затрат труда, будет равен произведению ∆L на предельный продукт труда MP_L.

Так как объем выпускаемой продукции должен ос­таться прежним, то можно записать:

,

т.е.

.

Однако

,

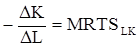следовательно,

Данная формула объясняет с математической точки зрения уменьшение предельной нормы технологичес­кого замещения. Допустим, что, согласно производ­ственной функции, предельные физические продукты капитала и труда уменьшаются сразу, как только их начинают использовать в процессе производства. Тог­да по мере увеличения затрат труда предельный физи­ческий продукт труда начинает сокращаться, т.е. чис­литель дроби будет уменьшаться. И, наоборот, по мере уменьшения количества капитала предельный про­дукт капитала будет возрастать, т.е. знаменатель дро­би будет увеличиваться, и в итоге MRTS_LKбудет уменьшаться. Будет ли производитель замещать один фактор другим и в каких пределах, зависит от цен на факторы производства, их производительности и типа производственной функции.

Выше были рассмотрены типичные производ­ственные функции, т.е. наиболее часто встречающие­ся. Однако есть и два особых случая. Первый — про­изводственные функции с совершенной взаимозаме­няемостью факторов (рис. 4.5).

Рис. 4.5. Производственная функция с совершенной

взаимозаменяемостью факторов производства.

Здесь наклон изокванты во всех точках одинаков и равен —1. Это значит, что одна единица капитала всег­да может заменить одну единицу труда. Более того, объем выпуска продукции может быть достигнут за счет использования только капитала (в точке А) или только труда (в точке В). Эти крайние случаи обычно нереальны, но иногда можно встретить производ­ственные процессы, близкие к ним. Например, сушка древесины под воздействием естественных сил приро­ды или токами высокой частоты.

Второй случай — производственные функции с фиксированной пропорцией между используемыми факторами производства (рис. 4.6). В данном случае замещение одного фактора другим невозможно. Уве­личение объема выпуска требует пропорционального роста затрат как труда, так и капитала, т.е. изокван­ты имеют форму прямого угла. L₁, K₁ —затраты тру­да и капитала, которые требуются для того, чтобы достичь объема производства Q₁. L₂, K₂— затраты, обеспечивающие выпуск продукции Q₂ и т.д. Точки А, В, Собозначают не просто комбинации факторов, позволяющие произвести данный объем продукции, а на­иболее эффективные технологические комбинации. Например, какую бы другую точку на изокванте Q_i мы ни взяли, она будет давать либо большие, чем в точке А, затраты труда (точка D),либо большие затра­ты капитала (точка Е),но выпуск продукции останет­ся прежним. Следовательно, на горизонтальных от­резках изоквант предельный физический продукт труда будет равен нулю. На вертикальных отрезках нулю будет равен предельный физический продукт капитала. Все это говорит о том, что при такой произ­водственной функции фирма ограничена в способе производства. Примером такой функции может слу­жить обслуживание троллейбусов. Нельзя увеличить численность водителей, не увеличивая число троллей­бусов, и наоборот.

Рис. 4.6. Производственная функция с фиксированной пропорцией

между используемыми факторами.

Таким образом, форма изокванты показывает воз­можности замещения факторов производства.