6.2.1. Для построения кода Шеннона–Фано все сообщения выписываются в порядке убывания их вероятностей. Записанные таким образом сообщения затем разбиваются на две по возможности равновероятные подгруппы. Всем сообщениям первой подгруппы присваивают цифру 1 в качестве первого кодового символа, а сообщениям второй подгруппы – цифру 0. Аналогичное деление на подгруппы продолжается до тех пор, пока в каждую подгруппу не попадёт по одному сообщению.
6.2.2. Для получения кода Хаффмана все сообщения выписывают в порядке убывания их вероятностей. Две наименьшие вероятности объединяют скобкой и одной из них присваивают символ 1, а другой – 0. Затем эти вероятности складывают, результат записывают в промежутке между ближайшими вероятностями. Процесс объединения двух сообщений с наименьшими вероятностями продолжают до тех пор, пока суммарная вероятность двух оставшихся сообщений не станет равной единице. Код для каждого сообщения строится при записи двоичного числа справа налево путём обхода по линиям вверх направо, начиная с вероятности сообщения, для которого строится код.
6.2.3. Универсальный код при неизвестной статистике сообщений для k- й группы состоит из двух частей: префикса и суффикса. Префикс содержит log(n+ 1) двоичных знаков. Он указывает, к какой группе сообщений принадлежит кодируемый блок. Суффикс содержит 
двоичных символов и указывает номер блока в группе. Суффикс вычисляется по правилу
. (6.3)
Для нахождения N (X) используется таблица биномиальных коэффициентов (треугольник Паскаля):
8 7 21 35 35 21 7 1 0
7 6 15 20 15 6 1 0
6 5 10 10 5 1 0
5 4 6 4 1 0
4 3 3 1 0 (6.4)
3 2 1 0
2 1 0
1 0
Пример 6.2. Для передачи по каналу связи без шумов используется код, состоящий из двух букв 
и 
появляющиеся с вероятностями 
и 
соответственно. Применить метод Шеннона–Фано к кодированию всевозможных однобуквенных, двухбуквенных и трёхбуквенных сообщений. Определить среднюю длину в каждом случае и результаты сравнить между собой.
Решение. Определим энтропию сообщений
Применяя метод Шеннона–Фано к двухбуквенному алфавиту получаем простейший код (табл. 6.2).
| Таблица 6.2 Код Шеннона – Фано для однобуквенных сообщений | Этот код требуется для передачи каждой буквы одного двоичного символа  что на 53 % больше минимально возможного значения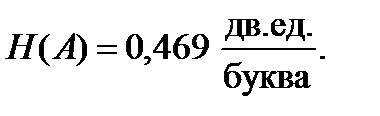 
Применим метод Шеннона – Фано к кодированию всевозможных двухбуквенных комбинаций (табл. 6.3).
| ||||||
| Буква | Вероятность | Код | |||||
| 0,9 | ||||||
| 0,1 | ||||||
| Таблица 6.3 Код Шеннона – Фано для двухбуквенных сообщений | Средняя длина кодового слова равна L = 1·0,81 + 2·0,09 +3·0,09 + 3·0,01=1,29 бит. Таким образом, на одну приходится 1,29/2 = 0,645 бит, что на лишь на 76 % больше значения 0,469. Произведем кодирование всевозможных трехбуквенных комбинаций (табл. 6.4). | ||||||
| Сообщение | Вероятность | Код | |||||
| 0,81 | ||||||
| 0,09 | ||||||
| 0,09 | ||||||
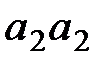
| 0,01 | ||||||
Таблица 6.4
| Сообщение | Вероятность | Код | Сообщение | Вероятность | Код |
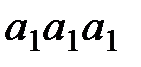
| 0,729 | 
| 0,009 | ||
| 0,081 | 
| 0,009 | ||
| 0,081 | 
| 0,009 | ||
| 0,081 | 
| 0,001 |
Средняя длина кодового слова здесь равна
L = 0,729 + 3 · 0,081 + 3 · 0,081 + 3 · 0,081 + 5 · 0,009 + 5 · 0,009 +
+ 5 · 0,009 + 5 · 0,009 = 1,598 бит.
Таким образом, на одну букву текста приходится в среднем 1,598/3 = 0,532 бит, что только на 6,3 % больше значения 
Ответ:кодирование блоками более выгодно, чем кодировать отдельные буквы.
Пример 6.3. Закодировать блок 
префиксным кодом при неизвестной статистике сообщений, если символ 
появляется с вероятностью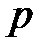 
, а 
– с вероятностью 
.
Решение. Определим число разрядов префикса
где Е – знак округления в большую сторону.
Вероятность слова определяется формулой
Тогда префикс будет 0011.
Число символов 
которые размещаются на местах: 
Находим номер блока 
Слагаемые в 
находим, используя таблицу дополнительных коэффициентов. Таким образом,
или в двоичной записи
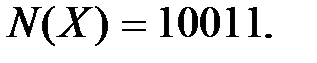
Следовательно, закодированный блок поступит в канал связи в виде
Пример 6.4. Из канала связи принята кодовая комбинация 
в префиксном коде с неизвестной статистикой сообщений. Необходимо декодировать данную кодовую комбинацию, если известно, что длина передаваемого блока 
а разрядность префиксов равна четырём.
Решение. По префиксу находим, что число букв 
а, следовательно, число букв в 
Находим максимальное число в пятом столбце треугольника Паскаля, не превосходящее число 19. Это 
следовательно, 
находим разность 19 – 6 = 13. Далее находим максимальное число четвёртого столбца, не превосходящее 13. Это 
т. е. 
Находим разность 13 – 5 = 8. Максимальным числом третьего столбца, не превосходящим 8, является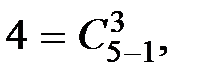 
т. е. 
Находим разность 8 – 4 = 4. Максимальное число второго столбца, не превосходящее 4, это 
т. е. 
Находим разность 4 – 3 = 1. Максимальное число первого столбца, не превышающее 1, это 
т. е. 
Следовательно, декодируемое сообщение имеет вид
,
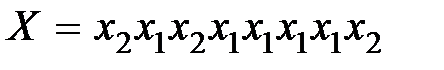что совпадает с условием примера 6.3.
Задачи и упражнения
6.3.1. Определить среднюю длину кодового слова при передаче xi сообщений длиной m i и вероятностями появления P (xi), указанными в табл. 6.5.
Таблица 6.5
| Сообщения | P (xi) | Кодовые слова |
| x 1 | 0,35 | |
| x 2 | 0,25 | |
| x 3 | 0,20 | |
| x 4 | 0,15 | |
| x 5 | 0,05 |
Ответ: L = 2,6 символа.
6.3.2. По каналу связи без помех передаются пять сообщений с вероятностями P (x 1) = 0,30; P (x 2) = 0,20; P (x 3) = 0,40; P (x 4) = P (x 5) = 0,05 в двоичном коде. Определить нижнюю границу средней длины кодового слова.
Ответ: L = 1,95 символа.
6.3.3. По каналу связи без помех передаются в двоичном коде пять сообщений с вероятностями P (x 1) = 1/2; P (x 2) = 1/4; P (x 3) = 1/8; P (x 4) = 1/16,
P (x 5) = 1/32. Определить нижнюю границу средней длины кодового слова и результаты сравнить с результатами задачи 6.3.2.
Ответ: L = 1,78; из сравнения следует, что если вероятности сообщений не являются целочисленными степенями числа m, точное достижение нижней границы невозможно.
6.3.4. Построить код Шеннона–Фано для восьми сообщений, имеющих следующие вероятности: 0,2; 0,2; 0,15; 0,13; 0,12; 0,10; 0,07; 0,03. Определить среднее число нулей, приходящихся на одно сообщение.
Ответ: L = 2,9 символа, что меньше, чем при равномерном кодировании (L = 3) и не очень далеко от энтропии: 
.
6.3.5. Для передачи по каналу связи без шумов используется код, состоящий из двух букв a 1 и a 2, появляющихся с вероятностями P (a 1) = 0,8 и P (a 2) = 0,2. Применить метод Шеннона–Фано к кодированию всевозможных однобуквенных, двухбуквенных и трехбуквенных сообщений. Определить среднюю длину в каждом случае и результаты сравнить между собой.
Ответ: L (1) = 1; L (2) = 0,78; L (3) = 0,728; H (A) = 0,722 
; кодирование блоками более выгодно, чем кодирование отдельных букв.
6.3.6. Построить код Хаффмана для восьми сообщений, имеющих следующие вероятности: 0,2; 0,2; 0,15; 0,13; 0,12; 0,10; 0,07; 0,03. Определить среднее число нулей и единиц, приходящихся на одно сообщение, и сравнить с результатами, полученными при решении задачи 6.3.4.
Ответ: L = 2,9; по экономичности в данном случае методы Шеннона –Фано и Хаффмана одинаковы.
6.3.7. Для передачи по каналу связи без шумов используется код, состоящий из двух букв a 1 и a 2, с вероятностями P (a 1) = 0,8 и P (a 2) = 0,2. Применить метод Хаффмана к кодированию всевозможных однобуквенных сообщений. Определить среднюю длину, скорость передачи, избыточность для каждого случая и сравнить их между собой, если длительности кодовых символов одинаковы и равны t = 10-6 с.
Ответ: L (1) = 1 бит; Rt 1 = 721900 бит/с; R (1) = 0,2781; L (2) = 0,78 бит; Rt 2 = 925513 бит/с; R (2) = 0,0042; L (3) = 0,728 бит; Rt 3 = 991620 бит/с; R (3) = 0,002.
Кодирование трёхбуквенных комбинаций даёт возможность приблизиться к максимальной скорости передачи информации.
6.3.8. По каналу связи передаются четыре сообщения кодовыми комбинациями
| x 1 | x 2 | x 3 | x 4 |
Определить, являются ли данные кодовые комбинации комбинациями префиксного кода.
Ответ: не являются.
6.3.9. По каналу связи передаётся последовательность 110110101100110010 комбинаций префиксного кода
| x 1 | x 2 | x 3 | x 4 | x 5 |
Произвести декодирование данной последовательности.
Ответ: x 1 x 3 x 4 x 1 x5x 2 x 4.
6.3.10. Алфавит кода состоит из двух символов x 1 и x 2, появляющихся с вероятностями p и q. Построить префиксный код, если кодовые комбинации передаются блоками, состоящими из n = 3 символов.
Ответ: 00, 01 00, 01 01, 01 10, 10 00, 10 00, 10 10, 11, где подчеркнуты префиксы.
6.3.11. Закодировать блок X = x 1 x 2 x 2 x 1 x 1 x 1 x 2 x 1 префиксным кодом при неизвестной статистике сообщений, если символы x 1 появляются с вероятностью p, а x 2 – c вероятностью q.
Ответ: X = 0011100001.
6.3.12. Из канала связи принята кодовая комбинация X = 0011100001 в префиксном коде с неизвестной статистикой сообщений. Декодировать данную кодовую комбинацию, если известно, что длина передаваемого блока равна n = 8, а разрядность префикса равна четырём.
Ответ: X = x 1 x 2 x 2 x 1 x 1 x 1 x 2 x 1.
7. Кодирование информации при передаче
по дискретному каналу с помехами
Основные формулы
Число разрешенных кодовых комбинаций, если число информационных символов равно k:
N 1 = 2 k. (7.1)
Общее число выходных кодовых комбинаций длиной n:
N 2 = 2 n. (7.2)
Число запрещённых кодовых комбинаций (исправляемых ошибок):
N 3 = 2 n – 2 k. (7.3)
Количество случаев появления необнаруживаемых ошибок
N 4 = 2 k (2 k – 1). (7.4)
Количество случаев появления обнаруживаемых ошибок:
N 5 = 2 k (2 n – 2 k). (7.5)
Общее количество возможных случаев передачи:
N 6 = 2 k · 2 n. (7.6)
Если производительность источника информации равна 
то скорость передачи после кодирования:
. (7.7)
Минимальное кодовое расстояние для обнаружения ошибок кратностью m:
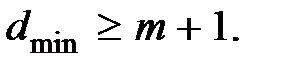(7.8)
Минимальное кодовое расстояние для исправления ошибок кратностью s:
(7.9)
Минимальное кодовое расстояние для обнаружения и исправления ошибок:
(7.10)
Число проверочных символов, если известна общая длина кодовой комбинации n:
(7.11)
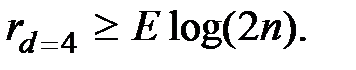(7.12)
Число проверочных символов, если известно число информационных символов:
(7.13)
где E – знак округления в большую сторону.
Пример 7.1. Для передачи сообщения используется код Хэмминга n = 7, k = 4. Определить число разрешённых кодовых комбинаций, общее число
n- разрядных кодовых комбинаций, число случаев появления необнаруженных ошибок, число случаев появления обнаруженных ошибок, число исправляемых ошибок и общее число возможных случаев передачи.
Решение. Число разрешённых кодовых комбинаций
Общее число кодовых комбинаций, которые могут быть представлены
n- разрядным кодом:
Число случаев появления необнаруживаемых ошибок:
Число случаев обнаруживаемых ошибок:
Число случаев исправленных ошибок:
Общее число возможных случаев передачи:
Пример 7.2. Определить минимальное кодовое расстояние d, если код должен обнаруживать ошибки кратностью 
исправлять ошибки кратностью S = 1 или обнаруживать и исправлять ошибки, указанной кратности.
Решение. При обнаружении ошибок кратностью m = 2
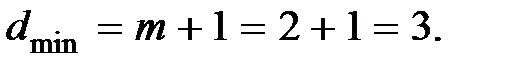
При исправлении ошибок кратностью S = 1.
При обнаружении и исправлении ошибок
