7.2.1. Образующая матрица М систематического кода состоит из единичной матрицы размерностью k ´ k и приписанной к ней справа матрицы дополнений размерностью k ´ r. Причём вес каждой строки матрицы дополнений должен быть не меньше, чем d min–1.
. (7.14)
Проверочная матрица N строится из образующей матрицы M следующим образом. Строками матрицы N являются столбцы матрицы дополнений образующей матрицы M. К полученной матрице дописывается справа единичная матрица размерностью r ´ r.
(7.15)
Единицы, стоящие в каждой строке, однозначно определяют, какие символы должны участвовать в определении значения контрольного разряда. Причем единицы в единичной матрице N определяют номера контрольных разрядов.
Декодирование систематических кодов осуществляется с учётом правил кодирования.
7.2.2 Проверочные элементы в рекуррентном коде формируются путём сложения по модулю два двух информационных элементов, отстоящих друг от друга на шаг сложения, равный b.
b= 2
Информационные элементы 0 0 0 0 1 1 1 0 1…
Проверочные элементы 0 0 1 1 0 1 0…
В данном коде после каждого информационного элемента следует проверочный элемент.
Процесс декодирования заключается в выработке проверочных элементов из информационных, поступивших на декодер, и их сравнении с проверочными символами, пришедшими из канала связи. В результате сравнения вырабатывается корректирующая последовательность, которая и производит исправление информационных элементов.
7.2.3. При построении свёрточных кодов поток данных разбивается на блоки длиной K 0 символов, которые называются кадрами информационных символов (КИС). КИС кодируются кадрами кодовых символов длиной n 0. При этом кодирование КИС в кадр кодового слова производится с учётом предшествующих m кадров информационных символов. Процедура кодирования, таким образом, связывает между собой последовательные кадры кодовых слов. Передаваемая последовательность становится одним полубесконечным кодовым словом.
Пример 7.3. Определить число контрольных символов в коде, позволяющем обнаруживать двойные ошибки, если число информационных символов k = 7.
Решение. Определим минимальное кодовое расстояние:
Тогда число контрольных символов
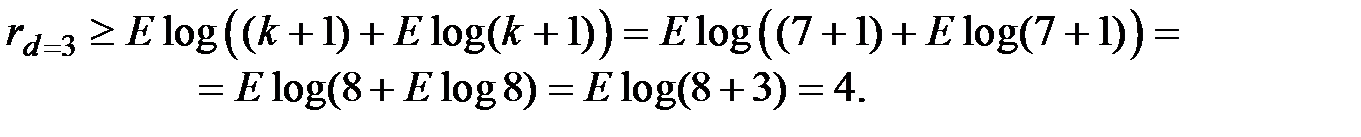
Пример 7.4. Получить алгоритм кодирования и декодирования кодовых комбинаций в систематическом коде, позволяющим обнаруживать двойные или исправлять одиночные ошибки, если число информационных символов 
Решение. Определим минимальное кодовое расстояние
Число контрольных символов
Строим образующую матрицу.
.
Из образующей матрицы строим проверочную
Из проверочной матрицы получаем алгоритм образования контрольных символов:
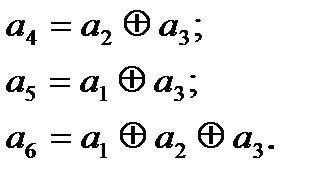
На приёмной стороне производятся 
проверки, которые составляются на основании алгоритма кодирования:
Синдром 
однозначно указывает на номер искажёния разряда. Рассмотрим всевозможные состояния :
Пример 7.5. На основании алгоритма, полученного в примере 7.4, закодировать кодовую комбинацию 
в систематическом коде с кодовым расстоянием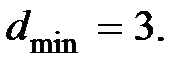 
Решение. Определим значения контрольных символов. Для чего пронумеруем символы входной комбинации:
Тогда
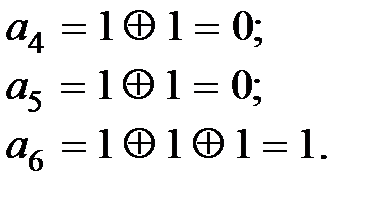
В результате получим кодовую комбинацию
Ответ: 
Пример 7.6. На основании алгоритма для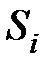 
проверок, полученных в примере 7.4, декодировать комбинацию 
Решение. Определим значения проверок:
Синдром 
указывает, что искажён символ a 3. Изменяем значение этого символа на противоположный и получаем исправленную кодовую комбинацию
что совпадает с кодовой комбинацией примера 7.5.
Ответ:искажён a 3, 
Пример 7.7. Закодировать в рекуррентном коде последовательность информационных символов 
с шагом сложения 
Решение. Кодирование произведем с помощью кодера, структурная схема которого представлена в [4]. Из схемы следует, что контрольные символы формируются с задержкой на b тактов. Поэтому перед информационной последовательностью, подлежащей кодированию, необходимо приписать 2 b нулей, т. е. четыре. Контрольные символы образуются путём сложения по модулю два двух информационных символов, расположенных на расстоянии b друг от друга. Процесс образования контрольных символов показан на рис. 7.1.
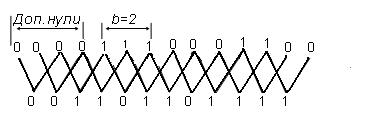
Контрольные символы
Рис. 7.1. Схема построения рекуррентного кода c b = 2
В данном коде после каждого информационного символа следует проверочный символ. Таким образом, на выходе получим последовательность символов 
.
Ответ: закодированная последовательность F (X)= 1010110100 0111100101.
Пример 7.8. Записать порождающий полином для импульсной переходной характеристики H = (11.00.10.11.00.00….).
Решение. H (x) = 1 + x + x 4 + x 6 + x 7.
Задачи и упражнения
7.3.1. По каналу связи передаются кодовые комбинации
x 1 = 1001001, x 2 = 1011011, x 3 = 0110101.
Определить минимальное кодовое расстояние.
Ответ: dmin = 2.
7.3.2. В качестве информационных последовательностей используется двоичный k = 2 разрядный код. В канал связи передаются последовательности длиной n = 9. Определить число разрешённых кодовых комбинаций; общее число n- разрядных кодовых комбинаций; число случаев появления необнаруживаемых, обнаруживаемых и исправляемых ошибок; общее число возможных случаев передачи.
Ответ: N 1 = 32, N 2 = 512, N 3 = 480, N 4 = 992, N 5 = 15360, N 6 = 16384.
7.3.3. Определить число контрольных символов (r) в коде, позволяющем исправлять одинарную ошибку или обнаруживать двукратные искажения, если число информационных символов k = 5.
Ответ: r = 4.
7.3.4. Определить число контрольных символов в коде, позволяющем обнаруживать двойные и исправлять единичные ошибки в кодовых комбинациях длиной n = 9.
Ответ: r = 5.
7.3.5. По условиям задачи 7.3.2 определить процент обнаруживаемых ошибочных кодовых комбинаций по отношению к общему числу возможных случаев передачи; процент исправления ошибочных кодовых комбинаций по отношению к числу обнаруживаемых ошибочных комбинаций, а также избыточность кода.
Ответ: процент обнаружения составит 93,75; процент исправления – 3,1; избыточность – 44 %.
7.3.6. Получить алгоритм кодирования и декодирования кодовых комбинаций в систематическом коде, позволяющем обнаруживать двойные или исправлять единичные ошибки, если число информационных символов k = 5.
7.3.7. На основании алгоритма, полученного в задаче 7.3.6, закодировать кодовую комбинацию G (X) = 11101 в систематическом коде с кодовым расстоянием d min = 3.
7.3.8. На основании алгоритма для Si проверок, полученных в задаче 7.3.6, декодировать кодовую комбинацию F' (X) = 111000011.
7.3.9. Закодировать в рекуррентном коде последовательность информационных символов 1111000011111100 с шагом сложения b = 3. Привести функциональную электрическую схему кодирующего устройства и с её помощью пояснить процесс образования контрольных символов.
Ответ: F (X) = 10101011010100011111101111110000.
7.3.10. Из канала связи с помехами поступила последовательность F' (X) = 1001011101010001111110111111000, закодированная в рекуррентном коде с шагом сложения b = 3. Декодировать данную последовательность. Привести функциональную электрическую схему декодера и с её помощью пояснить процесс декодирования.
Ответ: G (X) = 1111000011111100.
7.3.11. Из канала связи с помехами поступила последовательность 10010111010100011111101111110000, закодированная в рекуррентном коде с шагом сложения b = 3. Декодировать данную последовательность. Привести функциональную электрическую схему декодера и дать описание её работы.
7.3.12. Привести функциональную схему кодирующего устройства несистематического свёрточного кода, если частичные порождающие полиномы имеют вид P 1(x) = x 4 + x 3 + x + 1; P 2(x) = x 4 + x 2 + 1.
Закодировать с помощью данного устройства кодовую комбинацию G (x), соответствующую числу 22, записанному в двоичном коде. Записать импульсную переходную характеристику кодера.
7.3.13. Привести функциональную схему кодирующего устройства систематического свёрточного кода для порождающего полинома P (x) = x 4 + x 2 + x + 1.
Закодировать с помощью данного устройства кодовую комбинацию G (x), соответствующую числу 26, записанному в двоичном коде. Записать импульсную переходную характеристику кодера.
7.3.14. Привести функциональную схему кодирующего устройства несистематического свёрточного кода (8,4) для частичных порождающих полиномов P 1(x) = x 3 + x 2 + x + 1 и P 2(x) = x 3 + x 2 + 1. Проиллюстрировать работу кодера с помощью кодового дерева, если входная последовательность G (x) представляет число 21, записанное в двоичном коде.
7.3.15. Привести функциональную схему кодирующего устройства систематического свёрточного кода (8,4) для порождающего полинома P (x) = x 3 + x + 1. Проиллюстрировать работу кодера с помощью кодового дерева, если входная последовательность G (x) представляет число 27, записанное в двоичном коде.
7.3.16. Привести функциональную схему кодирующего устройства несистематического свёрточного кода (8,4) для частичных порождающих полиномов P 1(x) = x 3 + x 2 + x + 1 и P 2(x) = x 3 + x 2 + 1. Построить решётчатую диаграмму и с её помощью произвести кодирование информационной последовательности G (x), соответствующей числу 19, записанному в двоичном коде.
7.3.17. Привести функциональную схему кодирующего устройства систематического свёрточного кода (8,4) для порождающего полинома P (x) = x 3 + x + 1. Построить решётчатую диаграмму и с её помощью произвести кодирование информационной последовательности G (x), соответствующей числу 21, записанному в двоичном коде.