Основные формулы
Дифференциальная энтропия источника:
(.3.1)
Относительная дифференциальная условная энтропия источника:
(3.2)
Эпсилон-энтропия источника:
(3.3)
Эпсилон-энтропия для одного независимого отсчёта при гауссовском процессе Х (t) и E (t):
(3.4)
где 
и 
– среднеквадратическое значение сигнала и помехи соответственно.
Эпсилон-производительность источника при дискретном времени:
. (3.5)
где 
– скорость передачи отсчетов; 
– интервал дискретизации; 
– полоса частот сигнала X (t).
Если время непрерывное, то:
. (3.6)
Максимальное значение эпсилон-производительности имеет место, когда сигнал X (t) является гауссовским:
; (3.7)
, (3.8)
где 
– максимальная мощность помехи.
Объём информации, выдаваемый источником за время Т:
бит.(3.9)
Избыточность источника:
(3.10)
Количество информации, содержащееся в одной непрерывной случайной величине, относительно другой:
. (3.11)
Пример 3.1. Определить энтропию случайных величин равномерно распределенной на интервале с шириной 
Решение. Из условия задачи следует, что плотность вероятности 
, а энтропия
Пример 3.2. Вычислить дисперсию равномерного распределения на интервале 
.
Решение. На основании определения дисперсии имеем
Задачи и упражнения
3.2.1. Определить выигрыш в мощности при использовании источника с гауссовской плотностью распределения по сравнению с источником, имеющим в интервале равномерную плотность распределения.
Ответ: 
т. е. 42 %.
3.2.2. Определить энтропию случайной величины, распределённой по экспоненциальному закону:
Ответ: 
3.2.3 Определить количество информации I (X, Y) для системы (X, Y) гауссовских случайных величин:
.
Ответ: 
3.2.4.Определить ε производительность источника, формирующего со скоростью 
некоррелированные отсчёты стационарного нормального случайного сигнала с дисперсией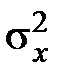 
.
Ответ: 
.
4. Информационные характеристики
непрерывных каналов
Основные формулы
Пропускная способность канала с дискретным временем:
. (4.1)
Пропускная способность канала с непрерывным временем:
. (4.2)
Число уровней, которое может быть различимо без ошибок:
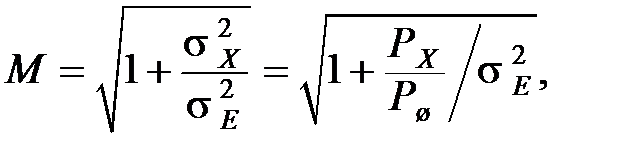(4.3)
где Рх и Р ш – мощность полезного сигнала и шума соответственно.
Приёмник не различает изменения входного сигнала меньше чем корень квадратный из мощности шума, т. е.:
. (4.4)
Наибольшее количество информации, переносимое импульсом, имеющим М различных уровней:
(4.5)
Пример 4.1. Аналоговый сигнал с амплитудой 2 В передаётся по каналу связи, в котором отношение сигнал/шум равно 20 дб. Определить абсолютную погрешность телеизмерения.
Решение. Если сигнал смешан с помехой, то амплитуда сигнала может быть измерена с точностью до эффективного значения напряжения. При этом погрешность оценки точного значения амплитуды равна 
.
Из соотношения
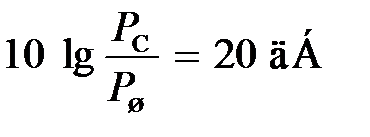
определим мощность шума
Тогда погрешность
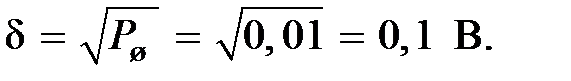
Пример 4.2. Определить пропускную способность канала связи при условии, что сигнал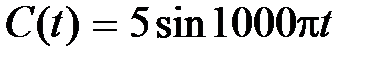 
должен быть восстановлен с погрешностью не большей чем 1 В.
Решение. Из условия задачи известно, что амплитуда сигнала 
В, а полоса частот 
Гц. Тогда пропускная способность
Задачи и упражнения
4.2.1. Определить объём информации, содержащейся в изображении из 500 строк по 500 элементов в каждой. Яркость каждого элемента передаётся восемью квантованными уровнями. Различные градации яркости равновероятны, а яркости разных элементов не коррелированы.
Ответ: 
.
4.2.2. Изображение задачи 4.2.1 должно быть передано по радиолинии, на входе которой действует белый гауссовский шум с удельной мощностью Р ОШ = 10-4 Вт/Гц. Ширина полосы пропускания приёмного устройства D F C = 1000 Гц. Время передачи 1 час. Определить минимально возможное значение мощности полезного сигнала на входе приёмника.
Ответ: РХ = 155·10-4 Вт.
4.2.3. Определить длину магнитной ленты для записи одного изображения, если энтропия изображения 
а по ширине ленты записывается 30 дв.ед. информации при плотности записи 
Ответ: L = 2000 мм.
4.2.4. Сигнал с амплитудой 1 В передаётся по каналу связи, в котором отношение сигнал/шум равно 10 дБ. Определить абсолютную погрешность телеизмерений.
Ответ: δ = 0,31 В.
4.2.5. По непрерывному каналу передаётся сигнал, спектр которого ограничен полосой частот 30 Гц. Определить пропускную способность канала связи таким образом, чтобы погрешность передаваемого сигнала не превышала 1 %.
Ответ: 
4.2.6. Непрерывный канал связи с пропускной способностью 
предназначен для передачи квантованного сигнала с полосой частот 5 Гц. Определить число различных уровней измеряемого сигнала и погрешность измерений.
Ответ: М = 16, δ = 6,3 %.
4.2.7. По радиолинии, на входе которой действует гауссовский шум с удельной мощностью 10-8 Вт/Гц, передаётся 1024 сообщения в течение 1·10-1 с. Определить минимальную мощность полезного сигнала на входе приемника, если полоса пропускания приемника равна 100 Гц.
Ответ: Р cmin = 10-6 Вт.
4.2.8. Отношение сигнал/шум в линии связи равно 10-1, а полоса пропускания канала связи 1 кГц. Определить пропускную способность канала связи.
Ответ: 
4.2.9. Определить пропускную способность канала связи при условии, что сигнал sin500p t должен быть восстановлен с погрешностью не большей чем 0,57 В.
Ответ: 
5. Информационные характеристики дискретных
каналов связи
Основные формулы
Скорость передачи информации:
, (5.1)
где t – длительность передаваемых сигналов.
Пропускная способность канала связи:
. (5.2)
Пропускная способность бинарного канала связи:
, (5.3)
где Р – вероятность перехода одного символа в другой.
Объём сигнала:
. (5.4)
где 
– превышение сигнала над помехой;
ТХ – время передачи сигнала;
FX – полоса частот сигнала.
Объём канала:
, (5.5)
где ТК – время использования канала;
FK – полоса пропускания канала;
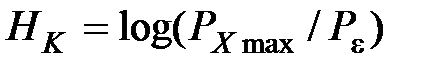– допустимая энергетическая нагрузка.
Пример 5.1. По каналу связи передаются двоичные 8-разрядные сообщения, вероятность появления нулей P (0) = 0,6. Время передачи одного сообщения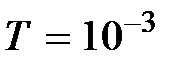 
с. Определить скорость передачи и пропускную способность канала связи.
Решение. Пропускная способность будет определяться выражением
Скорость передачи сообщений с учётом вероятности состояния каждого элемента будет равна
Пример 5.2. Количество сообщений, передаваемых с контролируемого пункта, о состоянии четырех объектов одинаково. Наблюдением установлено, что в среднем объект 1 включен в течение 80 % всего времени, объект 2 – 40 %, объект 3 – 60 %, объект 4 – 20 %. В остальное время объекты отключены. Определить скорость передачи информации и пропускную способность канала связи, если длительность одного сообщения 10-3 с.
Решение. Исходя из одинакового количества сообщений о состоянии объектов, можно записать, что 
Из статистики наблюдений можно записать выражения для определения вероятности того, что объекты находятся во включенном состоянии:
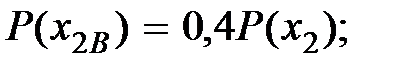
Результаты расчёта вероятностей того, что объекты находятся во включённом или отключённом состоянии, сведём в табл. 5.1.
Таблица 5.1
Вероятности 
и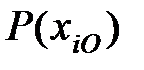 
| xi | x 1 B | x 1 O | x 2 B | x 2 O | x 3 B | x 3 O | x 4 B | x 4 O |
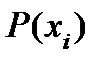
| 0,2 | 0,05 | 0,1 | 0,15 | 0,15 | 0,1 | 0,05 | 0,2 |
Тогда скорость передачи информации будет равна
Пропускная способность в этом случае будет равна
где М = 8 – общее число состояний системы (четырёх объектов).
Пример 5.3. По дискретному каналу связи с помехами передаётся кодовое сообщение 1110011110. Вероятность искажёния одиночных сигналов
,
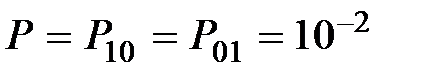а длительность элемента кода 10-3 с. Определить скорость передачи и пропускную способность канала связи.
Решение. Пропускную способность канала связи определим из выражения:
Скорость передачи
где 
Задачи и упражнения
5.2.1. В информационном канале используется алфавит с четырьмя различными символами. Длительность всех символов одинакова и равна t = 1 мс. Определить пропускную способность канала при отсутствии шумов.
Ответ: 
5.2.2. В информационном канале используется сменно-качественный код, при котором запрещается передача подряд двух одинаковых символов. Алфавит кода состоит из четырёх различных символов. Вероятности передачи всех разрешённых пар символов одинаковы. Длительности всех символов также одинаковы и равны t = 1 мс. Определить скорость передачи информации.
Ответ: 
5.2.3. В дискретном канале для передачи сообщений используются три различных символа с длительностями t1 = t2 = 10 мс и t3 = 20 мс. Определить пропускную способность канала.
Ответ: 
5.2.4. В канал связи передаются сообщения длиной n = 10 элементов, каждый из которых может принимать m = 4 состояния с вероятностями Р 1 = 0,2; Р 2 = 0,3; Р 3=0,1; Р 4 = 0,4. Время передачи одного сообщения t = 0,1 с. Определить скорость передачи информации и пропускную способность канала связи.
Ответ: 
.
5.2.5. По бинарному каналу передаются сообщения: 1110011101, 1110000001. Длительность каждого элемента сообщения t = 10 мс. Определить скорость передачи каждого сообщения и пропускную способность двоичного канала.
Ответ: 
5.2.6. В канал связи передаются сообщения от эргодического источника, вырабатывающего m = 3 элемента. В кодовых комбинациях запрещена передача двух одинаковых элементов. Вероятность передачи всех разрешённых кодовых комбинаций длиной n = 3 одинакова. Длительность каждого элемента t = 10 мс. Определить скорость передачи информации и пропускную способность канала связи.
Ответ: 
5.2.7. В бинарном канале вероятности подавления и воспроизведения ложного сигнала одинаковы и равны Р 10 = Р 01 =Р = 10-3. Длительности символов одинаковы и равны t = 1 мс. Определить пропускную способность бинарного симметричного канала.
Ответ: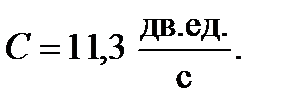 
5.2.8. По линии связи с помехами передаётся четыре сообщения. Ансамбль объединения описывается табл. 5.2. Длительность сообщения t = 2 мс. Определить скорость передачи сообщений и пропускную способность канала связи.
Таблица 5.2
| yj | xi | |||
| x 1 | x 2 | x 3 | x 4 | |
| y 1 | 0,1 | 0,05 | 0,05 | 0,15 |
| y 2 | 0,03 | 0,05 | 0,1 | 0,04 |
| y 3 | 0,07 | 0,03 | 0,05 | 0,06 |
| y 4 | 0,07 | 0,05 | 0,1 |
Ответ: 
5.2.9. По дискретному каналу связи с помехами передаётся кодовое сообщение 1100110011. Вероятность искажёния одиночных символов 
, а длительность элемента кода t = 1·10–2 с. Определить скорость передачи и пропускную способность канала связи.
Ответ: 
.
5.2.10. С контролируемого пункта передаются сообщения об изменении положения объектов. Каждый объект может находиться в одном из двух положений «включён» или «выключен». Наблюдением установлено, что из 50 переданных сообщений 40 относится к первому объекту, 2 – ко второму и 8 – к третьему. Объекты работают независимо друг от друга, а положения объектов равновероятны. Определить скорость передачи информации и пропускную способность дискретного канала, если длительность каждого сообщения 1 мс.
Ответ: 
.
5.2.11. Количество сообщений, передаваемых с контролируемого пункта, о состоянии трех объектов, одинаково. Наблюдением установлено, что в среднем объект 1 «включён» в течение 60 % всего времени, объект 2 – 30 %, а объект
3 – 40 %. В остальное время объекты «отключены». Определить скорость передачи информации и пропускную способность канала связи, если длительность одного сообщения 5 мс.
Ответ: 
. 
6. Кодирование информации при передаче
по дискретному каналу без помех
Основные формулы
Средняя длина кодового слова:
, (6.1)
где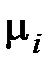 
– длина кодового слова, сопоставляемая xi сообщению.
При кодировании сообщений xi в алфавите, насчитывающем m символов, при условии отсутствия шумов средняя длина кодового слова определяется формулой
, (6.2)
где H (X) – энтропия сообщения.
Пример 6.1. Определите среднюю длину кодового слова и её нижнюю границу, а также вероятность появления нулей P (0) и единиц P (1), при передаче сообщений длиной 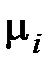и вероятностями появления сообщений 
, указанными в табл. 6.1.
Таблица 6.1
Ансамбль сообщений
| Cообщение |
| Код | 
|
| х 1 | 0,4 | ||
| х 2 | 0,3 | ||
| х 3 | 0,2 | ||
| х 4 | 0,1 |
Решение. Среднюю длину кодового слова определим из выражения
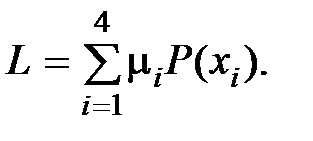
Подставив значения 
и из таблицы, получим:
Среднее число нулей
= 
Вероятность появления нулей P (0) = L (0)/ L = 1/2,4 = 0,417.
Среднее число единиц 
=2·0,4 + 1·0,3 + 1·0,2 + 1·0,1=
= 0,8 + 0,3 + 0,2 + 0,1 = 1,4 символа.
Вероятность появления единиц P (1) = L (1)/ L = 1,4/2,4 = 0,583.
Определим нижнюю границу средней длины кодового слова из выражения (6.2)
