Представление чисел и команд в ЭВМ (INFlesson5.doc).
Мысль выражать числа десятью знаками, придавая им, кроме значения по форме, ещё значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко прийти к этому методу, мы видим на примере величайших гениев греческой учёности Архимеда и Апполония, от которых эта мысль осталась скрытой.
Пьер Симон Лаплас
Понятие числа является фундаментальным как для математики, так и для информатики. Но если в математике наибольшее внимание уделяется методам обработки чисел, то для информатики нельзя обойти стороной методы представления чисел, так как именно они определяют необходимые ресурсы памяти, скорость и погрешность вычислений.
Изучая способы представления числовой информации необходимо знакомиться с правилами перевода одного представления числа в другое, пытаться понять, почему одно и то же число в различных ситуациях необходимо представлять по-разному. Приёмами представления чисел занимается специальный раздел теории чисел «Системы счисления».
Введено еще одно важное понятие – система счисления. Зачем она нужна? Что это вообще такое? Системы счисления – это системы, созданные человеком. Называют такие системы искусственными в отличие от естественных систем, созданных природой. К естественным (природным) системам относятся галактики, наша Солнечная система, человек как единое целое и так далее. К искусственным системам относятся города, заводы, система образования, национальные языки, то есть всё, что сделано людьми.
Искусственные системы можно разделить на
► материальные: автомобили, самолёты, дома, города, плотины и т.д.;
► общественные, то есть разные объединения людей: парламент, система народного образования, шахматный клуб и т.д.;
► информационные: национальные языки, компьютерная сеть Интернет, системы счисления и т.д.
Каждая искусственная система создаётся с определённой целью. Можно утверждать, что лучше та искусственная система, которая наилучшим образом обеспечивает достижение цели её создания.
Целью создания системы счисления является выработка наиболее удобного способа записи чисел. Система счисления позволяет отображать в компактной форме количественные сведения об объектах и манипулировать ими, используя достаточно простые правила.
Первые девять натуральных чисел мы обозначаем специальными знаками:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Поступать таким же образом со всеми встречающимися на практике числами, т.е. обозначать специальными знаками все встречающиеся числа, было бы неудобно. Даже если бы наши потребности ограничивались счётом в пределах тысячи, надо было бы запомнить тысячу специальных знаков. Естественно, что уже давно люди стали выбирать тот или иной ряд "ключевых", основных чисел и только их обозначать специальными знаками.
Системы счисления – это гениальное изобретение человечества. Для того чтобы сообщить о том, что сегодня две тысячи седьмой год на естественном языке, я вынужден использовать 16 символов (без учёта пробелов). С помощью языка чисел, можно то же самое изобразить четырьмя символами. Получается, что цифры представляют собой коды соответствующих слов, что подтверждается и тем, что номер года, записанный словами и числом, читается нами одинаково. Числа на разных естественных языках произносятся различным образом, а их запись и правила выполнения арифметических операций над ними одинаковы.
Понятие числа является фундаментальным как для математики, так и для информатики. Но если в математике наибольшее внимание уделяется методам обработки чисел, то для информатики нельзя обойти стороной методы представления чисел, так как именно они определяют необходимые ресурсы памяти, скорость и погрешность вычислений.
1. Система счисления – это способ изображения чисел и соответствующие ему правила действий над числами.
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные.
1.1 Непозиционные системы счисления.
Непозиционными системами счисления пользовались древние египтяне,
греки, римляне и некоторые другие народы древности. В непозиционных системах счисления от положения знака в записи числа не зависит величина, которую он (знак) обозначает.
До нас дошла римская система записи чисел (римские цифры), которая в некоторых случаях применяется до сих пор в нумерации (века, тома, главы книги). В римской системе в качестве цифр используются латинские буквы:
I V X L C D M
1 5 10 50 100 500 1000
Например, число ССXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
VI = 5 + 1 = 6, а IV = 5 – 1 = 4.
MCMXCVII = 1000 + (- 100 + 1000) + (- 10 + 100) + 5 + 1 + 1 = 1997.
Непозиционные системы счисления были более или менее пригодны для выполнения сложения и вычитания, но совсем не удобны при умножении и делении.
1.2 Позиционные системы счисления (ПСС).
Позиционные системы счисления удобны тем, что позволяют записывать сколь угодно большие числа с помощью небольшого количества цифр. Немаловажным преимуществом позиционных систем счисления являются достаточно простые алгоритмы выполнения арифметических операций над числами.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её позиции.
Количество используемых цифр называется основанием ПСС.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Её основание равно десяти, так как запись любых чисел производится с помощью десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Многие из нас эти значки, известные с детства, связывают с понятием "цифра". Тем не менее, в качестве цифр мы можем использовать любые значки. Да и цифр не обязательно должно быть десять.
Хотя десятичную систему принято называть арабской, но зародилась она в Индии, в V веке. В Европе об этой системе узнали в XII веке из арабских научных трактатов, которые были переведены на латынь. Этим и объясняется название "арабские цифры".
Позиционный тип десятичной системы легко понять на примере любого многозначного числа. Например, в числе 333 первая цифра означает три сотни, вторая – три десятка, третья – три единицы. Одна и та же цифра в зависимости от позиции в записи числа обозначает разные величины.
333 = 3 • 100 + 3 • 10 + 3.
Всякое десятичное число можно представить как сумму произведений составляющих его цифр на соответствующие степени десятки. То же самое относится и к десятичным дробям.
26, 387 = 2 • 101 + 6 • 100 + 3 • 10-1 + 8 • 10-2 + 7 • 10-3.
Это позволяет осуществить перевод чисел с основанием не равным 10 к десятичному представлению.
Для осуществления такого перевода необходимо записать исходное число в виде суммы произведений цифр числа на соответствующие степени основания и вычислить значение полученного числового выражения по правилам десятичной арифметики.
Примеры.
1. 432,325 → A10.
432,325 = 4*52 + 3*51 + 2*50 + 3*5-1 + 2*5-2 = 100 + 15 + 2 + 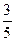 +
+  =
=
= 117  .
.
2. DF,4A16 → A10
DF,4A16 = 13*161 + 15*160 + 4*16-1 + A*16-2 = 208 + 15 + 
= 223 
Число «десять» - не единственно возможное основание позиционной системы. Известный русский математик Н.Н.Лузин так выразился по этому поводу: "Преимущества десятичной системы не математические, а зоологические. Если бы у нас на руках было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной системой".
Для записи чисел в позиционной системе с основанием n (n – обозначение основания ПСС) нужно иметь алфавит из n цифр. Обычно для этого при n ≤ 10 используют n первых арабских цифр, а при n > 10 к десяти арабским цифрам добавляют латинские буквы.
Приведем примеры алфавитов нескольких систем:
| Основание | Система | Алфавит |
| n = 2 | Двоичная | 0 1 |
| n = 3 | Троичная | 0 1 2 |
| n = 8 | Восьмеричная | 0 1 2 3 4 5 6 7 |
| n = 16 | шестнадцатеричная | 0 1 2 3 4 5 6 7 8 9 A B C D E F |
Основание системы, к которой относится число, обозначается подстрочным индексом к этому числу.
10110012, 36718, 3B8F16.
1.3 Перевод десятичных чисел в ПСС с основанием, не равным 10.
1.3.1 Перевод целых чисел.
- основание новой системы счисления выразить в десятичной системе
счисления и все последующие действия производить в десятичной системе счисления;
- последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
- полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
- Составить число в новой системе счисления, записывая его, начиная с последнего частного.
1.3.2 Перевод дробных чисел.
- основание новой системы счисления выразить в десятичной системе и все последующие действия выполнять в десятичной системе счисления;
- последовательно умножать данное число и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
- полученные целые части произведений, являющихся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
- составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Примеры перевода конкретных десятичных чисел представлены в приложении 1.
Приложение 1.

Рис. 1

Рис. 2
