КМ Лекция 2 Динамика
* символы, выделенные жирно – векторы
Если кинематика описывает законы движения, не интересуясь, почему движение происходит и почему именно так, а не иначе, то динамика изучает причины движения.
1. I закон Ньютона. Основная идея первого закона Ньютона принадлежит Галилею. Он первым поставил под сомнение принципы механики Аристотеля, который утверждал, что движется только то, что движимо. Галилей понял, что если исключить влияние на тело других тел, и прежде всего, трение, то тело будет двигаться прямолинейно и равномерно бесконечно долго и для этого не нужно его подталкивать. Такое движение он назвал движением по инерции.
1.1. Закон инерции Галилея: «Тело, на которое не действуют другие тела или действие этих тел взаимно уравновешено, называемое свободным телом, сохраняет состояние покоя или прямолинейного равномерного движения».
1.2. Ньютон добавил к этому, что такое движение по инерции происходит только относительно инерциальных систем отсчета. Существует также бесконечно много систем отсчета, называемых неинерциальными, в которых на тело не действуют другие тела, но оно движется ускоренно, правда это ускорение не зависит от величины тела и подчиняется простым законам, что позволяет свести движение в неинерциальных системах отсчета к инерциальным. Смысл первого закона Ньютона в том, что он постулировал, что «Существуют инерциальные системы отсчета, в которых тело движется в соответствии с законом инерции».
1.3. Если существует хотя бы одна инерциальная система отсчета, то их существует бесконечно много. Любая система, которая движется относительно инерциальной с постоянной скоростью (или покоится), является также инерциальной. В самом деле, если тело в первой системе движется с постоянной скоростью, то по закону о независимости перемещений и скоростей, оно будет и в другой системе двигаться с постоянной скоростью.
1.4. Законы Ньютона справедливы только для инерциальных систем отсчета. Если какая-либо система отсчета движется относительно инерциальной системы с ускорением, то эта система является неинерциальной. Тело, которое движется в инерциальной системе по инерции, относительно неинерциальной системы движется с ускорением. Поэтому в неинерциальной системе нарушается закон инерции, а также 2-й и 3-й законы Ньютона.
2. II закон Ньютона. Если на свободное тело действует другое тело, то его движения отклоняется от инерциального - тело приобретает ускорение. Разные тела, в зависимости от количества вещества в теле, по-разному реагируют на взаимодействие. Масса – это мера инертности тела, т.е. мера сопротивления тела действию на него другого тела.
Масса измеряется в килограммах. Килограмм — единица массы, равная массе международного прототипа килограмма. Эталон килограмма – это металлический цилиндр, масса которого примерно равна массе 1 дм3 дистиллированной воды при температуре 4⁰С. В 2019г был принят другой, более точный эталон килограмма, основанный на величине h – постоянной Планка
Сила – это мера взаимодействия тел. Второй закон Ньютона определяет силу, как векторную величину F =m a. Размерность силы [F] = кг м/сек2 =н (ньютон). Единица силы – 1н. Наличие силы можно обнаружить по ее проявлениям. Если сила действует на свободное тело, то оно двигается с ускорением. Если тело закреплено, то под действием силы оно изменяет форму – деформируется: вытягивается, сжимается, сгибается и т.д.
Смысл 2-го закона Ньютона в том, что ускорение, приобретаемое телом при взаимодействии тем больше, чем больше сила т.е. а ~ F, и тем меньше, чем больше масса, т.е. a ~ 1/m. При этом вектор ускорения направлен так же, как вектор силы. В результате 2-й закон приобретает вид равенства: a = F /m
2.1. Если тело взаимодействует одновременно с несколькими телами, то для вычисления их действия используется принцип суперпозиции сил. Он утверждает, что силы не влияют друг на друга и равнодействующая нескольких сил равна их векторной сумме: R = Σ F i. Это значит, что все силы, действующие на тело можно заменить на одну силу – равнодействующую- и действие этой силы эквивалентно действию всех сил, приложенных к телу. В этом случае II закон Ньютона имеет вид: R = m a.
2.2. Иначе 2-й закон Ньютона можно записать, используя понятия импульса. Пусть вектор F – равнодействующая сил, приложенных к телу. Запишем 2-й закон Ньютона так: F = m a = m Δ V /Δt, или F Δt = m Δ V. Считая, что масса величина постоянная можно записать, что m Δ V = m V2 – m V1 и F Δt = Δ(m V). Величина F Δt – называется импульс силы, а величина m V – называется импульс тела. Импульс, так же, как скорость – величина векторная.
Тогда 2-й закон Ньютона можно сформулировать следующим образом: изменение импульса тела равно импульсу, действующей на него силы. Формулировка закона в импульсной форме удобна тем, что она подходит для случая, когда масса тела изменяется, например, при приближении скорости тела к скорости света.
2.3. Все силы, фигурирующие в механике относятся к двум фундаментальным взаимодействиям: гравитационному и электромагнитному. Гравитационное – это сила тяжести, описываемая законом всемирного тяготения Ньютона. Электромагнитные силы – это силы взаимодействия заряженных тел и токов: Кулона и Ампера. К ним же относятся силы, порожденные межатомным взаимодействием: сила давления, все виды сил упругости, в том числе, сила реакции опоры и натяжения нити, а также все виды сил трения.
3. III закон Ньютона утверждает, что если тело А действует на тело В с какой-то силой, то тело В действует на тело А с силой одинаковой про величине, лежащей на той же прямой и противоположной по направлению, или иначе говоря, сила действия равна силе противодействия. Это закон, как и все прочие, получен экспериментально, и вытекает из экспериментального факта, что если взаимодействуют два тела с массами m1 и m2, то измеренные ускорения этих тел относятся друг к другу обратно пропорционально их массам, т.е.: a1/a2 = m2/m1, А значит, a1m1 = a2m2 и F1 = F2. В векторной форме F1 = - F2.
Заметим при этом, что сумма этих сил равная нулю, не является равнодействующей, потому что они приложены к разным телам.
4. Инерциальные и не инерциальные системы отсчета
4.1. Как было сказано, законы механики действительны только в инерциальных системах отсчета. Для них справедлив принцип относительности Галилея. Согласно ему, все механические явления в инерциальных системах отсчета при одинаковых начальных условиях протекают одинаково относительно своей системы отсчета. Из этого принципа следует, что невозможно внутри системы поставить опыт, который бы дал ответ, движется ли эта система или покоится.
4.2. Все величины в классической механике можно разделить на две группы: относительные и инвариантные (абсолютные). Относительные величины: координаты, перемещение, скорость зависят от системы отсчета. Инвариантные величины: силы, ускорения, массы, расстояния и размеры тел, а также время не зависят от системы отсчета.
4.3.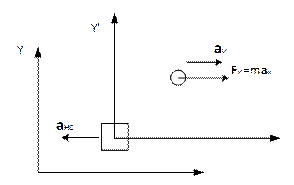 
Рассмотрим теперь, как выглядят законы механики в неинерциальной системе отсчета. Пусть X,Y – инерциальная система отсчета, X′,Y′ неинерциальная система отсчета, которая двигается относительно системы X,Y поступательно с ускорением анс. Тогдалюбое тело, которое в системе X,Y покоится или двигается с постоянной скоростью относительно системы X′,Y′ будет двигаться с ускорением аи = - анс. Это движение имеет вид, как будто на каждое тело действует сила Fи = m aи, создающая ускорение аи. Эту силу называют силой инерции.
Сила инерции – фиктивная сила. Настоящая сила является результатом взаимодействия двух тел. Сила инерции действует только на одно тело. У нее нет силы противодействия. Относительно инерциальной системы силы инерции нет. Мы вводим эту силу искусственно, чтобы свести законы механики в неинерциальной системе к законам Ньютона. 2-й закон Ньютона в неинерциальной системе отсчета имеет вид R + F и = m a, где R – равнодействующая всех настоящих сил. Или так: R – m a нс = m a
4.4. 
Рассмотрим еще один пример неинерциальной системы отсчета. Пусть есть некоторое тело, которое вращается в инерциальной системе отсчета с постоянной угловой скоростью ω. Рассмотрим движение тела массой m неподвижного относительно вращающегося тела и расположенного на расстоянии R от оси вращения. Точка где расположено тело m, двигаясь вместе с вращающимся телом будет двигаться с центростремительным ускорением ацс = ω2 R, направленным к оси вращения. Значит на тело m будет действовать сила инерции равная по модулю mацс и направленная от оси вращения. Эта сила действует только в неинерциальной системе отсчета и называется центробежная сила Fцб = mω2R = mV2/R
Часть II. Силы в механике
В механике различают силы:
1. Сила упругости. Она возникает, когда упругое тело деформирует внешняя сила. Сила упругости пытается восстановить прежнюю форму тела. В случае сопротивления плоской опоры, сила упругости направлена перпендикулярно плоскости опоры и называется сила нормального давления. Если внешняя сила вытягивает нить, гибкий трос и т.д., то сила упругости направлена вдоль нити и называется сила натяжения нити.
2. Сила тяжести. Она возникает в результате гравитационного притяжения тел друг к другу согласно Закону всемирного тяготения Ньютона. В простейшем случае сила тяжести на поверхности Земли – это сила притяжения тела к Земле. Она направлена вертикально вниз и равна Fт =mg, где g – 9.81 м/с2. Если тело находится под действием только силы тяжести, то по 2-му закону Ньютона, оно движется с ускорением a = Fт / m = mg / m = g. Т.е. тело движется с ускорением, не зависящим от его массы. Этот факт впервые экспериментально установил Галилей.
3. Сила трения. Существуют несколько разновидностей сил трения:
3.1. Сила трения покоя. Эта сила действует на тело, прижатое к другому телу силой, направленной перпендикулярно поверхности контакта (силой нормального давления). Она появляется только тогда, когда появляется т.н. сдвигающая сила, которая параллельна плоскости контакта и пытается сдвинуть одно тело относительно другого. Сила трения покоя направлена противоположно направлению сдвигающей силы и равна ей по величине. В результате сдвигаемое тело покоится. Чем больше сдвигающая сила, тем больше величина силы трения покоя. Она растет только до определенного максимального значения, а затем тело начинает двигаться и появляется новая разновидность силы трения:
3.2. Сила трения скольжения. Сила трения скольжения равна максимальному значению силы трения покоя, но в отличии от нее она направлена в сторону противоположную перемещению тела (а не сдвигающей силы). Сила трения скольжения не зависит от площади контакта двух тел (закон Кулона-Амантона), а определяется только свойствами поверхностей трущихся тел, и она пропорциональна силе нормального давления. Fтр.ск =Fтр. пок.макс = μN, где N – сила нормального давления. μ (или kтр) – коэффициент трения.
Природа силы трения покоя и скольжения двояка. С одной стороны – это влияние неровностей на трущихся поверхностях, чисто механического зацепления их друг за друга. С другой стороны – это результат притяжения друг к другу молекул на поверхностях трущихся тел. Поэтому очень глубокая шлифовка поверхностей может не уменьшить, а увеличить силы трения – молекулы контактируют друг с другом по всей поверхности и притягиваятся. При этом тела, как бы прилипают друг к другу.
3.3. Сила трения качения. Эта сила направлена, как и сила трения скольжения, в сторону, противоположную направлению движения. Однако, ее природа отлична от природы сил сухого трения. Она связана с деформацией поверхности колеса в месте его контакта с дорогой – колесо становиться в этом месте плоским, в результате точка приложения силы реакции опоры оказывается смещенной вперед и возникает ее компонента, направленная назад. Поэтому сила трения качения зависит от радиуса колеса: чем больше радиус, тем меньше влияние деформации на его движение и тем меньше сила трения.
Следует заметить, что на катящееся колесо, может действовать одновременно и сила трения покоя. Легко заметить, что в области контакта колеса с поверхностью, оно относительно нее неподвижно. В том случае, когда к колесу приложен момент силы, например, от двигателя транспортного средства и колесо пытается провернуться, т.е. в месте контакта с дорогой заскользить. При этом ему начинает мешать сила трения покоя. Благодаря ней у любого колесного транспорта возникает и сила тяги, и сила торможения.
3.4. Сила сопротивления. Предыдущие виды сил являются силами сухого трения, где обе трущиеся поверхности – твердые тела. При движении тела в жидкости или газе появляется сила влажного трения или сила сопротивления. Она возникает на поверхности твердого тела при его движении сквозь газ или жидкость и направлена всегда в сторону противоположную скорости тела. Характерной особенностью силы сопротивления является ее зависимость от скорости движения. При маленьких скоростях она растет пропорционально скорости в первой степени Fс = αV, а при больших – скорости в квадрате Fс = αV2. Все жидкости по отношению к силе сопротивления делятся на ньютоновские и реологические. В ньютоновских жидкостях тело начинает двигаться при самой маленькой, приложенной к нему силе. В реологических жидкостях имеется аналог силы трения покоя, когда, сдвинуть тело удается, только приложив к нему достаточную по величине силу.
Часть III. Сила упругости. Закон Гука
1. Твердые тела под действием внешней силы изменяют свою форму -деформируются. При этом тело сопротивляется этой деформации. Сила этого сопротивления называется силой упругости, и она по третьему закону Ньютона равна величине внешней – деформирующей – силы и направлена против нее. В зависимости от свойств твердого тела, после прекращения действия внешней силы оно ведет себя по-разному. Если деформация исчезает, то такая деформация называется упругой, если остается, то называется пластичной, а если уменьшается, но частично остается, то это упруго-пластичная или остаточная деформация.
2. Внутренняя причина возникновения сил упругости. Молекулы, из которых состоит любое вещество, при сближении отталкиваются, а при увеличении расстояния между ними – притягиваются. На некотором расстоянии существует точка равновесия молекулы со своими соседями, где молекула не отталкивается и не притягивается. В упругих телах молекулы расположены именно в таких точках, называемых узлами кристаллической решетки. Они колеблются, но в среднем эти точки не покидают.
Сдавливание тела внешней силой приводит к уменьшения расстояния между молекулами, что в свою очередь, приводит к возникновению сил отталкивания между ними. В совокупности силы отталкивания создают силу упругости, стремящуюся растянуть тело. Если внешняя сила растягивает тело, то возникают силы притяжения между молекулами и также появляется сила упругости, но стремящаяся сжать тело. Чем больше величина деформации, тем больше сила упругости, но до определенного предела. Начиная с какого-то момента, кристаллическая решетка перестраивается и возникает остаточная деформация, а начиная с какой-то величины силы, кристаллическая решетка разрушается совсем.
3. Закон Гука. Гук экспериментально вывел закон упругой деформации для протяженного тела: проволоки, стержня и т.д.:
Fу = - к Δх,
где к – коэффициент упругости тела, а Δх = хк – хн –изменение его длины, т.е. конечная длина минус начальная длина. Эта величина называется деформация. Знак минус показывает, что сила упругости всегда противоположна изменению длины тела.
Можно уравнение закона Гука преобразовать так, чтобы в нем фигурировали не абсолютные, а относительные величины.
Вместо силы упругости Fу использовать напряжение σ, т.е. силу упругости, действующую на единицу площади поперечного сечения σ = Fу /S, где S –площадь этого сечения.
Вместо деформации Δх использовать относительное удлинение ε=Δх/L, где L – длина тела, т.е. удлинение, приходящееся на единицу длины.
Тогда мы получим уравнение σS = - kεL или σ = - kL/S * ε. Е = kL/S – константа не зависящая, ни от длины стержня, ни от площади его сечения. Она называется модуль Юнга, обозначается буквой Е и является характеристикой материала, из которого сделано тело. В безразмерных величинах закон Гука имеет вид: σ = - E ε.
Зная модуль Юнга материала, длину и поперечное сечение стержня можно рассчитать его коэффициент упругости k = E S/L
4. 
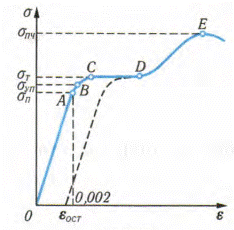Диаграмма растяжения. Диаграмма растяжения показывает, как меняется напряжение в образце, в зависимости от его относительного удлинения. Вот характерные точки на этой диаграмме
А – предел пропорциональности. Точка. где график перестает быть прямой.
В – Предел упругости. Если разгрузить образец до достижения этой точки, то он вернется к начальному размеру, а если после, то размер его увеличиться – появится остаточная деформация.
С – Предел текучести. Начиная с этой точки образец «течет», т.е его деформация растет без увеличения напряжения и после разгрузки она не уменьшается. Фактически, это область, где образец ведет себя, как пластичный. Для материалов, которые относятся к пластичным, эта область возникает уже при очень незначительной нагрузке.
Е – Предел прочности. После этой точки образец рвется.
Часть VI. Сила тяжести. Закон всемирного тяготения Ньютона
1. Гипотеза Ньютона. Силы, которые управляют движением тел Солнечной системы, и сила тяжести на Земле имеют общую природу. Эта догадка обрела математическую форму в виде закона всемирного тяготения. Рассуждения Ньютона при выводе этого закона основывались на изучении движения Луны и сравнении ее центростремительного ускорения с ускорением свободного падения тел на поверхности Земли.
Ускорение свободного падения на поверхности Земли равно g0 = 9,81м/с2 и направлено оно к центру Земли.
Ускорение Луны при движении по круговой орбите равно gл = ω2rл, где ω – угловая скорость Луны ω = 2π/Т, где Т =27,3 суток – период обращения Луны, а rл = 384 *106м – радиус орбиты Луны. Направлено ускорение Луны также к центру Земли. Расчет показывает, что gл примерно равно 60g0. А отношение радиуса орбиты Луны (расстояние между центром Земли и центром Луны) к радиусу Земли (расстоянию от центра Земли до предмета на ее поверхности) rл/Rз = 3600. Из этого Ньютон сделал предположение, что ускорение свободного падения обратно пропорционально квадрату расстояния между центром Земли и предметом, который она притягивает, т.е. g ~ 1/r2.
По 2-му закону Ньютона, который он к тому времени уже сформулировал, наличие ускорения означает наличие силы притяжения Луны к Земле Fл = Mлgл, где Mл – масса Луны. Следовательно, сила тяжести (назовем ее силой гравитации) Fг ~ mл. Но с другой стороны, не только Земля притягивает Луну, но и Луна притягивает Землю, причем по 3-му закону Ньютона с такой же по величине силой. Значит эта сила пропорциональна и массе Земли Mз. Значит, Fг ~ MзMл/rл2.
Из приведенных выше соображений Ньютон пришел к выводу, что «Все тела притягиваются друг к другу с силой прямо пропорциональной их массам и обратно пропорционально квадрату расстояние между ними ». Здесь под телами имеются в виду материальные точки. Однако Ньютон вычислил методом интегрирования, что однородная сфера и однородный шар притягивает любое тело, как материальная точка, имеющая его массу и расположенная в центре этого шара. В результате, Ньютон пришел к выводу, что сила тяжести тела на поверхности Земли определяется расстоянием от тела до центра Земли, т.е. радиусом Земли. Математически закон всемирного тяготения можно записать так: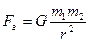 
, где G – константа, называемая гравитационная постоянная.
2. Измерение гравитационной постоянной. Гравитационную постоянную – одну из важнейших мировых констант - измерил английский физик Кавендиш только примерно через 100 лет после смерти Галилея. Для этого он использовал очень точные крутильные весы. На длинной стальной проволоке было уравновешено коромысло с двумя свинцовыми шариками на концах. Шарики одновременно приближались к двум огромным свинцовым шарам. Возникающая при этом сила гравитации поворачивало коромысло, скручивая стальную проволоку. С помощью этой установки удалось определить, что G = 6.67 × 10-11 м3 кг-1 с-2 . Знание гравитационной постоянной позволило вычислить массу Земли Mз. В самом деле: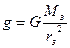 
, отсюда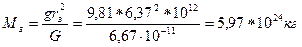 
3. Ускорение свободного падения. Равенство инертной и гравитационной массы. По своему смыслу масса тела в законе всемирного тяготения и во 2-м законе Ньютона существенно различны. В самом деле первая масса mг – это мера гравитационного взаимодействия тела, а вторая mи – мера его инертности. Считая, что это разные величины, вычислим ускорение свободного падения на поверхности Земли. Сила тяжести, действующая на тело с гравитационной массой mг равна 
. Согласно 2-му закону Ньютона ускорение свободного падения 
.
4. Согласно опытам Галилея, которые впоследствии многократно повторяли со все возрастающей точностью измерений, ускорение свободного падения не зависит от массы тела. Это возможно только если отношение mг/mи – константа. Если выбрать в качестве единицы измерения гравитационной массы ту же единицу, что и для инертной, т.е. килограмм, то mг = mи, т.е. инертная и гравитационная массы равны и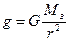 
. На поверхности Земли 
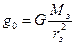. Разделив первое равенство на второе получим удобную формулу для ускорения свободного падения на удалении от Земли 
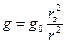. При r~= rз ускорение равно g ~= g0, а при удалении от Земли g уменьшается обратно пропорционально квадрату расстояния до центра Земли.
5. Движение спутника по круговой орбите. Условие движения тела по окружности: Fцс = Fт или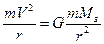 
. Откуда 
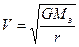. Для упрощения используем величину ускорения свободного падения у поверхности Земли g0. g0= GMз/Rз2 тогда GMз= g0 Rз2 и получим 
– это орбитальная скорость на орбите радиуса r. На небольшой высоте, где r ~ Rз орбитальная скорость называется первой космической скоростью: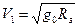 
= (9,81 м/с2 6,4 106м)1/2 = 7,9 103 м/с. Период движения спутника вокруг Земли на небольшой высоте T= 2πRз/V1 = 6,14 * 6,4 106 м /7.9 103 ~ 5000 с = 83 мин.
6. Законы Кеплера. Кеплер эмпирически открыл три закона небесной механики, касающиеся свойств движения планет вокруг Солнца еще до открытия Ньютоном закона всемирного тяготения. Все законы Кеплера были обобщением многочисленных наблюдений за движениями планет, выполненные астрономом Тихо Браге. Но они послужили Ньютону подтверждением его теории, т.к. выводились из нее теоретически.
6.1. Первый закон Кеплера. Планеты движутся вокруг Солнца по эллиптическим орбитам, причем Солнце находится в одном из фокусов эллипса.
6.2. Второй закон Кеплера. Радиус –вектор, проведенный от Солнца к планете за равные интервалы времени выметает равные площади.
6.3. Третий закон Кеплера. Квадраты периодов обращения планет вокруг Солнца относятся, как кубы их больших полуосей. Или, считая, что планеты движутся по окружностям, T12/T22 = r13/r23, где Т – период обращения планеты, а r – радиус орбиты. В самом деле: орбитальная скорость движения планеты по круговой орбите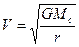 
, где Mс – масса Солнца, а r – радиус орбиты. Период обращения вычислим, разделив длину орбиты 2πr на орбитальную скорость. 
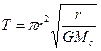или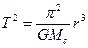 
. Запишем это равенство для двух произвольных планет, разделим одно на другое и получим 3-й закон Кеплера: T12/T22 = r13/r23
7. 
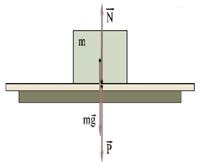Вес тела. Вес – это сила, действующая на опору или подвес, препятствующая падению тела под действием силы тяжести. Сила веса сжимает опору или растягивает подвес. Ей противостоит обычно сила упругости N. Для опоры, которая не имеет вертикального ускорения, сила веса равна по величине и направлению силе тяжести, но – существенно – она отличается от силы тяжести тем, приложена не к телу, а к опоре. Если опора перемещается с вертикальным ускорением, то вес тела изменяется. Вес P = - N по 3-му закону Ньютона. А по II закону Ньютона уравнение движение тела N +m g = m a, т.е. P = m (g – a). В скалярной форме, если ускорение направлено вниз, то P= m (g – a) и вес уменьшается. Если a=g то вес Р=0 – невесомость. Если ускорение направлено вверх, то P= m (g + a) и вес увеличивается – перегрузка.
Основные формулы
1. II закон Ньютона для силы F = m a и для импульса: Δ(m V) = F Δt
2. III закон Ньютона: сила действия равна и противоположна силе противодействия
3. Сила трения скольжения Fтр = kтр Q, где Q – сила нормального давления
4. Максимальное значение силы трения покоя равно kтр Q
5. Сила упругости пропорциональна и противоположна деформации Fу = - kx
6. Сила гравитации Fг = G m1 m2/ r2
7. Ускорение свободного падения на расстоянии r от центра Земли g = g0 rз2 /r2