Содержание
| Введение ………………………………………………………………………......... | |
| Исходные данные ………………………………………………………………….. | |
| 1. Определение кратчайшего расстояния между ГО и ГП …………………….... | |
| 1.1 Метод Хичкока ………………….………………………………………….. | |
| 1.2 Метод Фогеля ……………………………………………………………...... | |
| 1.3 Метод Моди..................................................................................................... | |
| 2. Оптимизация транспортной работы в Excel …................................................... | |
| 3. Планирование развозочных маршрутов методом Кларка-Райта...................... | |
| Заключение................................................................................................................. | |
| Библиографический список...................................................................................... |
Введение
Целью курсовой работы является оптимальное закрепление грузоотправителей (ГО) за грузополучателями (ГП) и оптимальное распределение груза для минимизации транспортной работы.
Определение кратчайших расстояний между пунктами ТС является важной практической задачей, так как дает возможность снизить транспортные издержки.
Линейное программирование интенсивно разрабатывалось во второй половине XX века. Основные идеи линейного программирования появились во время второй мировой войны, в связи с поиском оптимальных стратегий и проведения военных операций. С тех пор они нашли применение в промышленности, торговли и т.д.
Методами линейного программирования можно решить многие задачи, связанные с ограничением используемых ресурсов.
Частным случаем линейного программирования является транспортная задача. Она заключается в оптимальном закреплении ГО за ГП. Также транспортная задача применяется для маршрутизации перевозок грузов, а также для закрепления маршрутов.
Транспортная задача применяется не только на транспорте, но и в других отраслях экономики.
Исходные данные
Часть 1.
В городе N автотранспортное предприятие занимается перевозкой кирпича с заводов силикатного кирпича (Аn) на строительные площадки (Бn).
Потребности строительных площадок в кирпиче и возможности заводов по отгрузке приводятся в таблице 1.
Вариант 27

Таблица№1
| А1 | А2 | А3 | А4 | Б1 | Б2 | Б3 | Б4 | Б5 | Б6 | Б7 | |
| часть 1 | |||||||||||
| часть 2 |
Необходимо:
1. По модели транспортной сети и определить кратчайшие расстояния между грузоотправителями (ГО) и грузополучателями (ГП).
2. Оптимально закрепить ГП за ГО (минимизировать транспортную работу) используя:
- Метод Хичкока;
- Метод Фогеля;
- Метод Моди
Часть 2.
С товарного склада (А1) необходимо доставить по предприятиям – грузополучателям (А2, А3, А4, Б1, …Б7) пакетированный груз (крепеж, mбр=100 кг.). Грузовместимость используемых автомобилей 1000 кг (10 пакетов).
Необходимо:
Используя модель транспортной сети и кратчайшие расстояния между вершинами транспортной сети (из части 1), сформировать по критерию минимума суммарного пробега систему развозочных маршрутов при доставке груза с товарного склада (вершина А1) грузополучателям. Потребности в грузе приводятся в таблице 1.
Определение кротчайшего расстояния между ГО и ГП
Метод потенциалов.
Метод основан на приписывании вершинам временных пометок, которые дают верхнюю границу длины от начальной вершины до этой вершины.
Алгоритмопределения кратчайших расстояний методом потенциалов:
1. Начальной точке сети, за которую может быть принята любая из вершин, присваивают потенциал, равный нулю (vi = 0).
2. Определяют потенциалы соседних с начальной точкой вершин сети по формуле
vj = vi + lij,
где:
vi - потенциал предшествующей (соседней) вершины;
lij - длина звена, соединяющего вершины i и j.
Из них выбирают наименьший потенциал и присваивают его соответствующей вершине. Выбранный потенциал определяет кратчайшее расстояние от начальной точки до данной, на сети эту связь отмечают стрелкой.
3. Определяют потенциалы вершин, соседних с выбранной вершиной, и из всей совокупности потенциалов выбирают наименьший, который проставляют у соответствующей вершины и т.д.
Полное решение задачи включает столько этапов, сколько вершин включает транспортная сеть, поскольку каждый раз определяют кратчайшие расстояния от начальной точки до остальных.
Кратчайшие расстояния от точки А1.
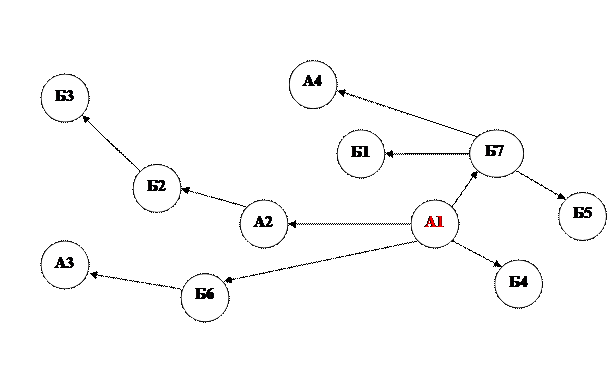
А1 - А1 = 0
А1 - A2 = 4
А1 - А3 = 5 + 7 = 12
А1 - А4 = 5 + 4 = 9
А1 - Б1 = 5 + 3 = 8
А1 - Б2 = 4 + 8 = 12
А1 - Б3 = 4 + 8 + 4 = 16
А1 - Б4 = 4
А1 - Б5 = 5 + 4 = 9
А1 - Б6 = 7
А1 - Б7 = 5
Полученная таблица кратчайших расстояний.
Таблица № 2
| А1 | А2 | А3 | А4 | Б1 | Б2 | Б3 | Б4 | Б5 | Б6 | Б7 | |
| А1 | - | ||||||||||
| А2 | - | ||||||||||
| А3 | - | ||||||||||
| А4 | - | ||||||||||
| Б1 | - | ||||||||||
| Б2 | - | ||||||||||
| Б3 | - | ||||||||||
| Б4 | - | ||||||||||
| Б5 | - | ||||||||||
| Б6 | - | ||||||||||
| Б7 | - |
Построение опорного плана методом двойного предпочтения.
Сначала просматривают все строки матрицы и в каждой из них отмечают элемент с минимальной стоимостью (*). Затем просматривают столбцы и также отмечают в них элемент с минимальной стоимостью (*). В клетки с двумя знаками (**) помещают максимально возможные перевозки.
L(x) = 4*60+5*80+16*80+4*20+12*20+11*10+14*20+5*20+5*20+4*40=2990 т*км
Таблица № 3
| ГО | ГП | вывоз, т | |||||||||||||
| Б1 | Б2 | Б3 | Б4 | Б5 | Б6 | Б7 | |||||||||
| А1 | ** | ||||||||||||||
| А2 | ** | * |   80 80
| ||||||||||||
| А3 | ** | * | ** | ||||||||||||
| А4 | * | ** | |||||||||||||
| ввоз, т |
Метод Хичкока
Алгоритм определения оптимальности: во всех загруженных клетках получаем нулевой потенциал, для этого по строчкам и столбцам таблицы, ко всем расстояниям, поставленным в верхних правых углах загруженных клеток, прибавляем такие числа, которые в сумме с расстояниями дают 0. Т. е. расстояние каждой загруженной клетки должно быть равно обратному значению суммы потенциалов строки и столбца, в которой находится данная клетка.
1) Определяя потенциалы для всех свободных клеток, находят для каждой свободной клетки сумму указанного в ней расстояния с ранее полученными по загруженным клеткам потенциалами строки и столбца
При решении задач на минимум оптимальный вариант получится в том случае, когда во всех загруженных клетках находится нулевой потенциал, а потенциалы не загруженных клеток являются положительными числами. Наиболее потенциальной клеткой является такая клетка, потенциал которой имеет наибольшее отрицательное значение.
Наибольшая потенциальная клетка получает загрузку, чтобы это сделать, необходимо перераспределить груз в таблице. Это выполняется следующим образом: количество загруженных клеток в предыдущем шаге должно равняться m+n-1, если количество загруженных клеток менее m+n-1, то недостающее число клеток получают путем загрузки соответствующего количества клеток нулями. Клетка, в которой поставлена загрузка равная 0, считается загруженной. Для наиболее потенциальной клетки строится контур. Строится контур так, чтобы все углы кроме одного располагались в загруженных клетках, а один единственный находился в свободной наиболее потенциальной клетке. При соблюдении этого правила для каждой свободной клетки можно построить только один единственный контур. Определяются положительные и отрицательные углы контура, считается, что первый положительный угол лежит в свободной клетке, для которой построен контур, отрицательные и положительные углы чередуются, и их количество должно быть равно. Выявляется наименее загруженная клетка, занятая отрицательным углом в нашем контуре. Количество груза указанное в этой клетке отнимается из всех клеток с отрицательными углами и прибавляется во все клетки с положительными углами. В результате одна или несколько ранее загруженных клеток становятся свободными, а наиболее потенциальная клетка становится загруженной.
Таблица № 4
| ГО | ГП | вывоз,т | потенциал | |||||||||||||
| Б1 | Б2 | Б3 | Б4 | Б5 | Б6 | Б7 | ||||||||||
| А1 |  3 3
|  5 5
| -6 | |||||||||||||
| А2 |  5 5
|  4 4
| -4 | |||||||||||||
| А3 | -7 | |||||||||||||||

| ||||||||||||||||
| А4 | -5 | |||||||||||||||
| ввоз, т | ||||||||||||||||
| потенциал | -4 |
L(x) =50*4+10*5+80*4+0*5+100*4+30*8+40*5+20*5+20*5+20*4=1690 т*км
Условие m+n-1 соблюдается- 7+4-1=10.
Решение является оптимальным, так как во всех загруженных клетках находится нулевой потенциал, а потенциалы не загруженных клеток являются положительными числами.