Мы будем использовать понятие интервала. Пусть 
- действительные числа, 
. Рассмотрим определения различных интервалов.
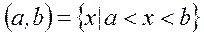- открытый интервал;
- замкнутый интервал.
Полуоткрытые (полузамкнутые) интервалы:
- интервал, открытый слева и замкнутый справа;
- интервал, открытый справа и замкнутый слева.
Полубесконечные интервалы:
, 
, 
, 
.
Напомним, что 
- это множество всех действительных чисел.
Пусть 
- действительное число, 
- положительное число. Открытый интервал 
называется 
- окрестностью числа 
. Окрестностью числа 
называется множество, которое содержит некоторую 
-окрестность этого числа.
Рассмотрим функцию y = f (x), x Î X и пусть x 1 Î X и x 2 Î X, причем x 1< x 2, тогда функция называется: монотонно возрастающей, если f (x 1) < f (x 2), монотонно убывающей, если f (x 1) > f (x 2), неубывающей, если f (x 1) £ f (x 2), невозрастающей, если f (x 1) ³ f (x 2).
Число A называется пределом функцииf (x) при x стремящемся к a, если при любом e > 0 существует такая окрестность точки a, что для любого x ¹ a из этой окрестности выполняется 
Если A является пределом функции 
в точке а, т.е. при 
, то это записывается так:
или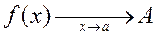 
.
Предел постоянной функции в любой точке равен этой же постоянной. 
Если функция f (x) имеет предел при x, стремящемся к a, то этот предел единственен.
Теоремы о пределах функции: Если при x ® a существуют пределы функций f (x) и g (x), то существуют также и пределы их суммы, произведения, частного в точке a, причем:
Следствие. Постоянный множитель можно вынести за знак предела:
.
Пример. Вычислить пределы:
1) 
,
2) 
.
Функция y = f (x) называется бесконечно большой в точке a, если
, аналогично определяется, если 
, т.е. 
Функция y = f (x) называется бесконечно малой в точке a, если 
, аналогично 
.
Очевидно, что если f (x) – бесконечно большая функция при x ® a, то функция 
- бесконечно малая при x ® a.
При решении конкретных задач в отсутствии неопределённостей пользуются таблицами наиболее часто встречающихся пределов, значения которых много раз проверены:
1) 
,
2) 
,
3) 
,
4) 
,
5) 
, где с = const,
6) 
.
Бесконечно малые и бесконечно большие функции обладают свойствами:
Сумма, разность, произведение конечного числа бесконечно малых функций при 
также является бесконечно малыми функциями при 
.
Пример. Функция 
является бесконечно малой в точке 
, т.к. 
. А функция 
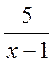является бесконечно малой при , так как 
и бесконечно большой при x=1 так как 
.
Если 
и 
– б.м. величины при 
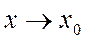, то выражение 
при 
называется неопределенностью вида 
, если же 
и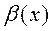 
– б.б. величины при 
, то выражение 
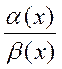при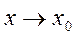 
называется неопределенностью вида 
, а выражение 
– неопределённостью вида 
.
Раскрытие неопределенностей.
Раскрыть неопределённость – значит найти предел соответствующего выражения, если он $. Для раскрытия неопределённости используют следующие приемы, если функциональное соответствие представляет собой отношение двух многочленов 
,и 
, то следует числитель и знаменатель разделить на 
, где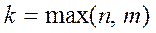 
.
Пример. Вычислить предел 
