МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Старооскольский технологически институт им. А.А. Угарова (филиал) федерального государственного автономного образовательного учреждения высшего образования
«Национальный исследовательский технологический университет «МИСиС»
(СТИ НИТУ «МИСиС»)
Кафедра высшей математики и информатики
Методические указания по выполнению домашнего задания
по курсу «Информатика»
для студентов бакалавриата очной формы обучения специальностей:
22.03.02 – Металлургия,
15.03.02 – Технологические машины и оборудование
13.03.01 – Теплоэнергетика и теплотехника
08.03.01 – Строительство
Старый Оскол
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Электронные таблицы Excel – это программа, предназначенная для автоматизации решения задач, в которых исходные данные и результаты должны быть представлены в табличном виде.
Рабочий лист в Excel, как правило, имеет матричную структуру – состоит из ячеек, расположенных на пересечении строк и столбцов. Ячейки рабочего листа имеют заданный формат, который устанавливается командой ФОРМАТ=> Ячейки.
В ячейки рабочего листа вводится два вида данных: константы и формулы. Константы делятся на числовые, текстовые, логические, типа дата/время. Числа включают цифры и символы-разделители: десятичная точка, процент, знак числа, денежное обозначение (например, р. или $). Текст представляет собой последовательность букв, цифр, специальных символов.
Массив – это множество ячеек, содержимое которых обрабатывается как единое целое. Такие ячейки могут указываться как именованный диапазон, например A1:D4 (см. рис. 1).

Рис. 1. Массив ячеек A1:D4.
|
|
Формула массива – это формула, оперирующая с одним или несколькими массивами. Для работы с формулами массива необходимо знать следующее:
· признаком формулы массива являются фигурные скобки в начале и конце формулы;
· фигурные скобки вводятся нажатием комбинации клавиш Ctrl+Shift+Enter;
· при редактировании формул фигурные скобки исчезают, для восстановления фигурных скобок нужно повторно нажать вышеуказанную комбинацию клавиш.
Например, чтобы найти матрицу, обратную к исходной матрице (см. рис. 2), мы используем формулу массива, примененную к массиву A1:C3.

Рис. 2. Нахождение обратной матрицы.
Аналогично можно перемножать матрицы (см. рис. 3), в частности перемножение матрицы D1:F3 на вектор G1:G3.

Рис. 3. Использование формулы массива при перемножении матриц.
Процедура Поиск решения представляет собой мощный вспомогательный инструмент для выполнения сложных вычислений. Она позволяет по заданному значению результата находить множество значений переменных, удовлетворяющих указанным критериям оптимизации. Пользователь может установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета.
Используя процедуру Поиск решения, найдем корень уравнения x4 - x3 - 2x2 +3x – 3= 0 на отрезке [- 2; -1].
Значение х запишем в ячейку А1, в ячейку В1 напишем формулу для вычисления f(x), выполним команду Сервис – Поиск решения, затем в открывшемся окне диалога запишем ограничения на значения интервала решения (см. рис. 4).

|
|
Рис. 4. Диалоговое окно Поиск решения.
Нажав кнопку Выполнить, найдем значение корня (см. рис. 5).

Рис. 5. Найденное значение корня уравнения в ячейке A1.
Аналогично, находится максимальное и минимальное значение функции на отрезке [- 2; -1] (см. рис. 6 и 7).

Рис. 6. Диалоговое окно Поиска максимального значения.

Рис. 7. Найденное максимальное значение функции.
Для построения графика функции следует предварительно построить таблицу значений аргумента х и соответствующих им значений функции f(x). Далее с помощью Мастера диаграмм можно построить график заданной функции (см. рис. 8).

Рис. 8. График функции f(x)=x4 - x3 - 2x2 +3x – 3
Процедура Подбор параметра позволяет в формуле при некоторых известных переменных найти варьируемое значение неизвестного параметра.
Например, расчет накопительного фонда для обучения производится по формуле S = V0 (1 + P)N, где V0 - размер вклада, который будет помещён в банк на определенный срок N под заданный процент P. Используя команду Сервис - Подбор параметра, определим: какой должна быть сумма вклада V0, чтобы при ставке 3% годовых через пять лет получить сумму 100000рублей. Решение этой задачи приведено на рисунках 9 и 10.

Рис. 9. Использование процедуры Подбор параметра.

Рис. 10. Решение, найденное подбором параметра.
Таблицы подстановки
С помощью таблиц подстановки пользователь может оценить влияние нескольких параметров на некоторую величину. В Excel создавать таблицы подстановки позволяет команда Таблица подстановки из меню Данные.
Перед вызовом этой команды в ячейку рабочего листа следует ввести формулу, отражающую исследуемую зависимость. Если создается таблица для одной переменной, формула должна содержать ссылку на одну ячейку таблицы, в которую при формировании таблицы подстановки будут подставляться значения из списка. Если же создается таблица для двух переменных, формула должна включать ссылки на две ячейки.
|
|
Исходные значения необходимо вводить в виде списка. Если таблица подстановки создается для исследования зависимости некоторой величины от одного параметра, список исходных значений можно разместить либо в строке, либо в столбце рабочего листа. Если параметров два, значения одного из них должны находиться в столбце, значения другого — в строке, а результаты вычислений - на пересечении соответствующих строки и столбца. Используя данные из предыдущего примера, с помощью таблицы подстановки определим суммы выплат для разных процентных ставок и сроков вклада при условии, что сумма вклада известна.
Задание. Используя команду Таблица подстановки с одним и двумя входами, определить:
a) Какими должны быть суммы выплат в конце периода при изменении процентной ставки от 3% до 6,0% с шагом 0,25%.
b) Какими должны быть суммы выплат в конце периода при изменении процентной ставки от 3% до 6,0% с шагом 0,25% и при сроках вклада 5, 10, 15, 20 лет.
Решение первой задачи приводится на рисунках 4.11, 4.12 и 4.13.
В ячейки B7:B19 занесем значения процентов от 3% до 6,0% с шагом 0,25%. В ячейку С7 запишем формулу для нахождения суммы выплаты в конце периода. Затем выделим интервал ячеек В7:С19 и выполним команду Данные – Таблица подстановки, далеев диалоговом окне укажем ячейку $В$3 для подстановки значения по строкам. В результате получим искомое решение.
Решение второй задачи приводится на рисунках 4.14, и 4.15. В ячейку В7 запишем формулу для нахождения суммы выплаты в конце периода. В ячейки С7:F7 занесем значения сроков вклада 5, 10, 15, 20 лет. Далее выделим интервал ячеек В7:F20 и выполним команду Данные – Таблица подстановки, затемв диалоговом окне укажем ячейку $В$3 для подстановки значения по строкам и ячейку $В$4 для подстановки значения по столбцам. В результате получим суммы выплат с вариациями процентной ставки и периода вложения денег.
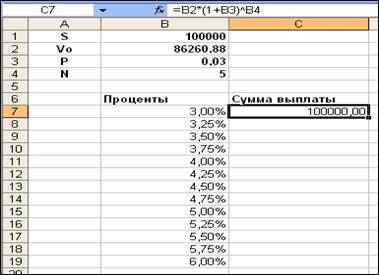
Рис. 11. Введение формулы для суммы выплаты.

Рис. 12. Использование Таблицы подстановки с одним входом.

Рис. 13 Решение, полученное с использованием Таблицы подстановки с одним входом.

Рис. 14. Использование Таблицы подстановки с двумя входами.

Рис. 15. Решение, полученное с использованием Таблицы подстановки с двумя входами.
Список Excel – это электронная таблица, содержащая данные определенной структуры. Каждый столбец списка содержит данные одного типа. Столбцы списка называются полями. Каждая строка списка образует запись. Список должен отвечать определенным требованиям:
1) содержать фиксированное количество полей (столбцов), которые и определяют структуру записи БД;
2) первая строка списка должна содержать имена полей, они же – названия столбцов;
3) имя поля должно размещаться в одной ячейке.
Эффективным средством представления информации, хранящейся в базах данных, является сводная таблица. При создании сводной таблицы (Данные/Сводная таблица или инструмент Мастер сводных таблиц) можно «сказать» Excel, какие поля должны быть отражены в таблице, задать макет таблицы и тип выполняемых вычислений.
Мастер сводных таблиц осуществляет построение сводной таблицы в несколько этапов (см. рис. 4.16, 4.17, 4.18, 4.19).
1-ый этап. Указание вида источника сводной таблицы:
· Использование списка или базы данных
· Использование внешнего источника данных
· Использование нескольких интервалов консолидации
· Использование данных из другой сводной таблицы.

Рис. 16. Первый шаг Мастера сводных таблиц.
2-ый этап. Указание интервала ячеек для построения сводной таблицы.
Если предварительно установить курсор в список, для которого строится сводная таблица, интервал ячеек будет автоматически указан. Для ссылки на закрытый интервал другой рабочей книги нажимается кнопка Обзор и в диалоговом окне выбираются диск, каталог и файл закрытой рабочей книги, вводятся имя рабочего листа и интервал ячеек.

Рис. 17. Второй шаг Мастера сводных таблиц.
3-ый этап. Построение макета сводной таблицы и выбор места расположения сводной таблицы.

Рис. 18. Третий шаг Мастера сводных таблиц.
Нажав кнопку Макет можно построить структуру сводной таблицы.
Размещение полей выполняется путем их перетаскивания при нажатой левой кнопке мыши в определенную область макета.
Каждое поле размещается только один раз в областях страница, строка или столбец, По этим полям (они называются группировочными полями) можно формировать группы и получать итоговые значения в области данные. В области данные, могут находиться поля произвольных типов, одно и то же поле может многократно размещаться в области данные. К данным применяются различные функции – сумма, количество, среднее значение, максимальное или минимальное значение и другие.

Рис. 19. Макет сводной таблицы.
В макете сводной таблицы можно выполнить настройку параметров полей путем двойного щелчка кнопки мыши.
После завершения построения сводной таблицы могут измениться исходные данные, Для обновления данных в сводной таблице следует выполнить команду Данные =>Обновить данные.
Например, имеется список данных о сотрудниках института:
| Кафедра | ФИО сотрудника | Должность | Разряд | Коэффициент надбавки к зарплате | Оклад | Дата рождения |
| АП | Иванова С.М. | Доцент | 1,2 | 11.3.1965 | ||
| АП | Смирнов А.С. | Профессор | 1,5 | 12.6.1951 | ||
| АП | Антонова Е.В. | Преподаватель | 1,2 | 13.4.1967 | ||
| АП | Хмелев Н.Ю. | Доцент | 1,5 | 05.9.1965 | ||
| АП | Гавшина Е.И. | Профессор | 1,5 | 26.6.1967 | ||
| ТОММ | Топоров К.Д. | Преподаватель | 1,5 | 23.7.1955 | ||
| ТОММ | Петров К.Г. | Доцент | 1,2 | 03.7.1963 | ||
| ТОММ | Кузьмин К.Е. | Преподаватель | 1,2 | 04.11.1968 | ||
| ТОММ | Голиков И.А. | Преподаватель | 1,5 | 23.12.1966 | ||
| ТОММ | Ульянов А.П. | Доцент | 1,5 | 06.4.1955 |
Сводная таблица, где в качестве страницы выбрано поле Кафедра, в качестве строки выбрано поле Должность, в качестве данных – поле ФИО сотрудника и к данным применена функция Количество, приведена на рисунке 20.Она показывает, сколько сотрудников есть на кафедре АП в разрезе должностей.
Меняя страницы, можно посмотреть то же самое для других кафедр и для всего института в целом. Сделав двойной щелчок по ячейке А3, вы можете поменять функцию обработки в сводной таблице, например можно выбрать функцию Сумма, примененную к столбцу Оклад. Полученная сводная таблица (см. рис. 21) показывает общую сумму окладов в разрезе должностей и сотрудников выбранной кафедры.
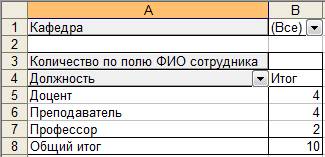
Рис. 20. Сводная таблица.

Рис. 21. Сводная таблица с функцией Сумма по полю Оклад.
Для построения диаграммы можно также воспользоваться Мастером диаграмм, который работает в 4 шага. На первом шаге указывается тип диаграммы, на втором - область данных, на третьем – параметры диаграммы, и на четвертом шаге – место расположения диаграммы (на новом листе или на имеющемся).
Диаграмма должна быть осмысленной и отображать данные вашей сводной таблицы (см. рис. 22).

Рис. 22. Круговая диаграмма на основе данных сводной таблицы.
Методические указания к решению задачи 2
Если непрерывная функция f(x) принимает на концах отрезка [a, b] значения разных знаков, то есть f(а)* f(b)<0, то внутри этого отрезка содержится, по крайней мере, один корень. Этот корень будет единственным, если производная f¢ (x) существует и сохраняет постоянный знак внутри интервала (a, b).
Пример. Требуетсяотделить корни уравнения x4 - x3 - 2x2 +3x – 3 = 0
Составим таблицу знаков функции f(x), полагая x равным:
a) критическим значениям функции (корням производной) или близким к ним;
b) граничным значениям (исходя из области допустимых значений неизвестного).
Вычислим: f¢ (x) = 4 x3 - 3x2 - 4x + 3
Находим корни производной: x = -1, x = 1, x =3/4
В этих же точках, которые называются точками перегиба, функция имеет экстремумы.
Используя найденные значения корней, проверим значение функции в промежутках между ними.
| x | - ¥ | - 1 | 3/4 | + ¥ | |
| знак f(x) | + | - | - | - | + |
Из таблицы видно, что функция меняет знак два раза, значит, уравнение имеет два действительных корня:
x1 Î (- ¥, -1), x2 Î (1, + ¥).
Уменьшим промежутки, в которых находятся корни:
| x | - 2 | - 1 | ||
| знак f(x) | + | - | - | + |
Следовательно, x1 Î (- 2; -1), x2 Î (1; 2).
Используя процедуру Поиск решения, найдем все корни уравнения x4 - x3 - 2x2 +3x – 3= 0
Значение х запишем в ячейку А1, в ячейку В1 напишем формулу для вычисления f(x), выполним команду Сервис – Поиск решения, запишем в окне диалога ограничения на значения интервала решения.

Нажав кнопку Выполнить, найдем значение первого корня.

Аналогично можно найти значение второго корня и три значения функции в точках экстремумов.
ЗАДАНИЕ:
Найти решение следующих пяти задач в табличном процессоре MS Excel согласно варианту. Решение, все его шаги и используемые формулы описать в пояснительной записке к каждой задаче домашнего задания (возможно принтование экранов Excel с решением и кратким пояснением в доступном для чтения масштабе).
ЗАДАЧА 1
1. Вычислить значения функции  для всех значений переменной х на отрезке [a; b] с шагом h при заданном значении k.
для всех значений переменной х на отрезке [a; b] с шагом h при заданном значении k.
Решение должно быть получено в виде таблицы:
| № | x | k | f(x) | y(x) |
2. На основании данных таблицы построить совмещенные графики функций f(x) и y(x).
ВАРИАНТЫ
| № | a | b | h | k | f(x) |
| 1,5 | 0,05 | sin(x) - 1/x | |||
| -1 | 0,1 | cos(x) - 1/(x+2) | |||
| 1,2 | 0,02 | 4x2 - cos(x) – 4 | |||
| 0,1 | cos(x) + 1/(x-2) | ||||
| -1 | 0,1 | ex + 2sin(x) | |||
| -1 | 0,1 | x + 1/(x2+1) | |||
| -1 | 0,1 | ex + x | |||
| -2 | -1 | 0,1 | cos(x)-1/(x-2) | ||
| 0,1 | e -x - ln(x) | ||||
| 0,1 | e -x - x | ||||
| 0,1 | cos(x) - x2 | ||||
| -2 | 0,2 | x3 - x2 + 3 |
ЗАДАЧА 2
- Отделить корни алгебраического или трансцендентного уравнения f(x)=0, предварительно проанализировав область определения аргумента x.
- Используя процедуру Поиск решения найти:
все корни данного уравнения, все имеющиеся экстремумы (минимальные и максимальные значения) данной функции.
3. Построить график функции f(x) на конечном отрезке.
ВАРИАНТЫ
| № варианта | Уравнение f(x)=0 |
| x3 - 3x2 - 4x+ 1=0 | |
| x3 – 21x + 7=0 | |
| 10 x = e-x | |
| 2x3 + 2x -1=0 | |
| x3 - 3x – 1=0 | |
| x3 - 3x2 +1 = 0 | |
| x3 +6x2 + 9x+ 1= 0 | |
| e-x = 2 – x2 | |
| x3 - 12x + 5=0 | |
| x3 - 2x +4=0 | |
| x3 + x2 + 2 = 0 | |
| x3 - x2 – 2 = 0 |
ЗАДАЧА 3
- Решить систему линейных алгебраических уравнений Ax = b с использованием математических функций для нахождения обратной матрицы A-1 и произведения матриц A-1 * b.
- Выполнить проверку найденного решения путем перемножения матриц A и x и сравнения полученного значения с b.
ВАРИАНТЫ
| № варианта | Матрица коэффициентов системы А | Столбец свободных членов b |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |
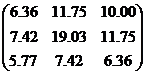
| 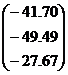
| |

| 
| |

| 
| |
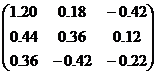
| 
| |

| 
| |

| 
|
ЗАДАЧА 4
2. Расчет накопительного фонда для обучения производится по формуле:
S = V0 · (1 + P)N , где V0 - размер вклада (в рублях), который будет помещён в банк на определенный срок N (количество лет) под заданный процент P.
3. Вычислить:
a) фонд для обучения в конце периода.
b) во сколько раз увеличится вклад за указанный срок;
4. Используя команду Подбор параметра, определите:
a) какой должна быть сумма вклада V0, чтобы при ставке P1 % годовых через N лет получить сумму S.
b) каким должен быть срок вклада, чтобы при сумме вклада V0 и ставке P % в год получить сумму S.
5. Используя команду Таблица подстановки с одним и двумя входами, определить:
a) Какими должны быть суммы выплат в конце периода при изменении процентной ставки от P % до P1 % с шагом h %.
b) Какими должны быть суммы выплат в конце периода при изменении процентной ставки от P % до P1 %с шагом h % и при сроках вклада 5, 10, 15, 20 лет.
ВАРИАНТЫ
| № варианта | V0 | N | P | P1 | S | h |
| 3,00 | 4,00 | 0,2 | ||||
| 3,25 | 4,25 | 0,25 | ||||
| 3,50 | 4,50 | 0,25 | ||||
| 3,75 | 4,75 | 0,25 | ||||
| 4,00 | 5,00 | 0,2 | ||||
| 4,25 | 5,25 | 0,25 | ||||
| 4,50 | 5,50 | 0,25 | ||||
| 4,75 | 5,75 | 0,25 | ||||
| 5,00 | 6,00 | 0,2 | ||||
| 5,25 | 6,25 | 0,25 | ||||
| 5,50 | 6,50 | 0,25 | ||||
| 5,75 | 6,75 | 0,25 |
ЗАДАЧА 5
- Создать базу данных (БД) согласно варианту (не менее 10 записей).
- Создать сводную таблицу для БД.
- Показать использование различных функций в сводной таблице.
- На основе данных сводной таблицы построить круговую диаграмму.
ВАРИАНТЫ
| № варианта | Исходные данные для БД |
| Списочный состав института: Кафедра, ФИО сотрудника, должность, разряд, коэффициент надбавки к зарплате, оклад, дата рождения, возраст | |
| Сведения о коммунальных платежах за текущий месяц: Улица, дом, квартира, количество человек, площадь, газ, холодная и горячая вода, отопление, сумма, дата оплаты. | |
| Сведения о поставках оборудования: Код оборудования, количество, цена, наименование поставщика, сумма заказа, сумма оплаты | |
| Сведения о расходах горючего по хозяйству: Наименование материала, цена, количество, дата поступления, регион поставки, номер автомашины | |
| Сведения о готовой продукции: Код изделия, марка, наименование, серийный номер, цена, дата поступления, количество | |
| Сведения о книгах: Название книги, ФИО автора, год издания, издательство, цена, дата покупки, число страниц | |
| Сведения о заказах на автомобили и клиентах: Модель, мощность двигателя, цвет, количество дверей, заводская цена, цена продажи, дата заказа, скидка | |
| Сведения о зарплате: Наименование цеха, ФИО сотрудника, должность, разряд, месяц, премия, сумма к выдаче | |
| Сведения об имуществе фирмы: Наименование имущества, код помещения, серийный номер, цена, дата покупки, место покупки, оценка | |
| Сведения о расчетах с сотрудниками: ФИО сотрудника, должность, адрес, месяц, начислено, удержано, сумма к выдаче | |
| Сведения о пациентах медицинского центра: № карточки, ФИО пациента, адрес, телефон, ФИО врача, диагноз, дата посещения, сумма оплаты | |
| Сведения об абонентах телефонной сети: ФИО абонента, номер телефона, адрес, тарифный план, месяц, сумма к оплате |