Плоским температурным полем называется такое поле, в котором температура изменяется только в направлении осей 
и 
, а в направлении оси z остается постоянной. В ограждающих конструкциях зданий плоское температурное поле характерно при наличии в них элементов каркаса, прокладных рядов, перемычек и пр., когда их протяженность значительно превышает толщину ограждения. В этом случае, принимая длину элементов каркаса бесконечно большой, будем иметь плоское температурное поле, в котором распределение температуры во всех плоскостях, параллельных плоскости поперечного сечения рассматриваемого элемента, будет одинаково.
Дифференциальное уравнение плоского температурного поля приведено в главе I [уравнение (4)]. Интегрирование этого уравнения в общем виде представляет весьма сложную задачу, которая еще более усложняется наличием в пределах поля материалов с различными коэффициентами теплопроводности. Задача значительно упрощается при решении уравнения (4) в конечных разностях. При этом дифференциальное уравнение заменяется системой обыкновенных линейных уравнений, неизвестными в которых будут значения искомой функции в точках
| Лист |
| КР-2069059-270109-081405-2010 |
.
В конечных разностях уравнение (4) имеет вид:
где 
вторые конечные разности функции 
по х и по у соответственно.
Выписывая их подробно, получим (рис.20):
откуда, решая полученное уравнение относительно 
, будем иметь
т.е. в однородном поле температура в каждом узле сетки должна равняться средней арифметической температур четырех соседних узлов.
Если поле неоднородно, т. е. в нем имеются материалы с различными коэффициентами теплопроводности, поступаем следующим образом. Накладываем на исследуемую конструкцию квадратную сетку с расстояниями между ее узлами таким образом, чтобы узлы сетки располагались по возможности в тех точках, в которых требуется определять температуру. Кроме того, направление одних нитей сетки должно быть параллельным, а других — перпендикулярным основному направлению теплового потока. На рис. 21 приведен пример наложения сетки на стальную колонну двутаврового сечения. Вертикальные нити сетки направлены параллельно оси колонны; одна из горизонтальных нитей совпадает с наружной поверхностью полки двутавра.
Рассмотрим узел с температурой . Квадрат, в центре которого находится этот узел, получает (или отдает) тепло в направлении к точкам, расположенным в четырех соседних узлах сетки, имеющих температуры 
, 
, 
и 
| КР-2069059-270109-081405-2010 |
| Лист |
Обозначив коэффициенты теплопередачи буквами k с соответствующими индексами, получим:
· количество теплоты, передаваемой в направлении от узла х, у к узлу с температурой 
:
;
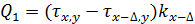· количество теплоты, передаваемой в направлении от узла х, у к узлу с температурой :
;
· количество теплоты, передаваемой в направлении от узла х, у к узлу с температурой :
;
· количество теплоты, передаваемой в направлении от узла х, у к узлу с температурой :
;
| КР-2069059-270109-081405-2010 |
| Лист |
Из условия теплового баланса сумма этих количеств теплоты должна быть равна нулю, т.е.
Решая это уравнение относительно , получим окончательно
Это и есть общая формула для вычисления температуры во всех узлах сетки.
В частном случае, если все четыре квадрата, примыкающие к узлу с температурой лежат в пределах одного материала (однородное температурное поле), то 
и в этом случае формула (33) обращается в формулу (32).
Коэффициенты теплопередачи между узлами сетки определяются следующим образом (см. рис. 21). Принимаем, что от узла с температурой к узлу с температурой 
передача тепла происходит только по квадрату abdc. Тогда коэффициент теплопередачи 
определится как величина, обратная сопротивлению теплопередаче квадрата abdc. Сопротивление теплопередаче этого квадрата определяется как ограждение, в котором однородность материала нарушена в перпендикулярном и параллельном тепловому потоку направлениях.
Передача тепла от узла с температурой , к узлу с температурой происходит по квадрату hknm, а к узлу с температурой — по квадрату ghml. Сопротивление теплопередаче этих квадратов определяется, как для двухслойной стены.
| КР-2069059-270109-081405-2010 |
| Лист |
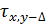передача тепла происходит по квадрату cdfe, сопротивление теплопередаче которого определяется, как для стены, состоящей из двух материалов, каждый из которых имеет толщину, равную толщине стены. Для квадратов, в которые входит только один материал,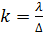 
, где 
коэффициент теплопроводности материала, Вт/(м 
); 
расстояние между узлами сетки, м.
Если узел с температурой лежит в плоскости, граничащей с воздушной средой, то коэффициент теплопередачи к воздуху будет равен соответствующей величине коэффициента тепловосприятия 
или теплоотдачи 
. В этом случае величины k к соседним узлам, лежащим в этой плоскости, берутся с коэффициентом 0,5 на основании того, что в направлении к этим узлам передача тепла по материалу будет происходить только по площади, равной половине квадрата сетки, а по воздуху, в котором окажется вторая половина квадрата, передачи тепла не будет.
Иногда удобнее для расчета температурного поля пользоваться прямоугольной сеткой (рис. 22). Располагая нити сетки более густо в области поля, в которой пас наиболее интересует распределение температуры, например в местах теплопроводных включений, и более редко в остальной области поля, удается значительно сократить число узлов сетки, а следовательно, и число расчетных уравнений.
| КР-2069059-270109-081405-2010 |
| Лист |
При прямоугольной сетке коэффициенты теплопередачи между узлами определяются с учетом площади, по которой передается тепло; размер поля в направлении оси z принимается равным 1 м.При этом, если узлы сетки лежат в области одного материала, имеющего коэффициент теплопроводности 
(однородное поле), то по рис. 22 получим следующие значения величин коэффициентов теплопередачи между узлом с температурой 
и соседними узлами:
к узлу 1 – площадь теплопередачи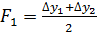 
;
коэффициент теплопередачи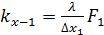 
;
к узлу 2 
; 
;
к узлу 3 
; 
;
к узлу 4 
; 
;
Если поле неоднородно, то коэффициенты теплопередачи между узлами сетки определяются так же, как и при квадратной сетке, но с умножением их на соответствующие площади теплопередачи F, м2. При этом размерность коэффициентов теплопередачи между узлами прямоугольной сетки будет Вт/ 
| КР-2069059-270109-081405-2010 |
| Лист |
Температурное поле, полученное для данных значений температур внутреннего и наружного воздуха, легко пересчитывается и для других значений этих температур па основании того, что разность температур любой точки поля и внутреннего или наружного воздуха изменяется пропорционально изменению разности температур внутреннего и наружного воздуха.
Температурное поле дает возможность точно определить величину среднего сопротивления теплопередаче ограждения 
. Для этого вычисляется средняя температура одной из поверхностей ограждения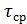 
. Количество тепла, проходящего через эту поверхность:
,
где 
— температура воздуха около данной поверхности, ;
— коэффициент теплоотдачи воздух — поверхность, Вт/(
С другой стороны, количество тепла, проходящего через ограждение
где 
— разность температур внутреннего и наружного воздуха, .
Из условий равенства величин 
получим окончательно:
Формула (34) дает возможность точно определить сопротивление теплопередаче любого сложного ограждения, а так же ограждений, отличающихся от плоской стенки (простенки с выступами, перекрытия с кессонными потолками и пр.)