ПРОСТРАНСТВЕННОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ.

Дифференциальное уравнение пространственного темпера­турного поля приведено в главе I [уравнение (3)]. Решение это­го уравнения в конечных разностях принципиально остается та­ким же, как и для плоского температурного поля, только вместо квадратной сетки поле разбивается пространственной решеткой на кубики с ребрами длиной . В однородном поле температуры в узлах решетки должны удовлетворять условию:

 

 

где — температуры в шести соседних узлах решетки, .

КР-2069059-270109-081405-2010

Лист

При неоднородном поле необходимо учитывать величины ко­эффициентов теплопередачи между узлами решетки аналогично тому, как это делается при плоском температурном поле. В этом случае расчетные формулы получаются аналогичными форму­ле (33), но с шестью членами в числителе и в знаменателе пра­вой части.

Следовательно, с теоретической точки зрения расчет прост­ранственного температурного поля затруднений не представляет. Однако практически расчет пространственного температурно­го поля значительно усложняется и становится чрезвычайно тру­доемким, что резко ограничивает область его применения.

Задача расчета пространственного температурного поля рез­ко упрощается в одном частном случае, а именно - когда в нем имеется ось симметрии. В строительной практике этому усло­вию соответствуют случаи, когда в ограждающей конструкции есть болтовые крепления, а также балки, заделанные в стену, вкладыши, шпонки, которые без большой погрешности можно привести к круглому сечению.

Дифференциальное уравнение температурного поля с осью симметрии должно быть выражено в цилиндрических координатах. Для однородного температурного ноля его дифферен­циальное уравнение в цилиндрических координатах имеет вид:

где — температура в любой точке поля, ; r — расстояние точки от оси симметрии, м; — координата точки по оси симметрии, м.

Если на температурное поле наложить плоскую квадратную сетку с расстояниями между узлами таким образом, чтобы одна из нитей сетки совпала с осью симметрии, то в конечных разностях уравнение (36) можно представить в виде:

 

КР-2069059-270109-081405-2010

Лист

откуда температура в любом узле сетки

 

 

Полученное уравнение для температуры любой точки поля, отстоящей на расстоянии r метров от оси симметрии, отличается от уравнения (32) для плоского температурного поля добавоч­ным членом По мере удаления точки от оси симметрии величина радиуса r возрастает, а следовательно, уменьшается величина добавочного члена. При добавоч­ный член обращается в нуль, и тогда уравнение (37) обращает­ся в уравнение (32) для плоского температурного поля, что справедливо и для = 0.

Формула (37) неприменима для точек, лежащих на оси сим­метрии, так как при этом = 0 и = 0 и добавочный член обращается в неопределенность вида 0/0. Для расчета тем­ператур точек, лежащих па оси симметрии, можно применить общую формулу (35) для пространственного температурного по­ля. В этом случае, учитывая, что температуры в соседних узлах, лежащих на осях х и у, будут равны, из уравнения (35) полу­чим:

ng w:val="EN-US"/></w:rPr><m:t>6</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:color w:val="000000"/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:vertAlign w:val="superscript"/><w:lang w:val="EN-US"/></w:rPr><m:t>. (38)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">

При неоднородном температурном поле с осью симметрии, а также при наложении прямоугольной сетки, температуры в уз­лах, около которых нарушена однородность поля (при прямо­угольной сетке во всех ее узлах), определяются по формуле (33). Коэффициенты теплопередачи, входящие в эту формулу определяются следующим образом:

 

Лист

КР-2069059-270109-081405-2010

1. В направлении радиуса – как цилиндрической стенки толщиной, равной расстоянию между узлами, по формуле:

где z – расстояние между узлами сетки в направлении оси z, м; коэффициент теплопроводности материала, расположенного между узлами, Вт/(м ); s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> радиусы цилиндрической стенки, м.

Если между узлами расположены два материала с коэффициентами теплопроводности то коэффициент теплопередачи между узлами определяется как для двухслойной цилиндрической стенки по формуле:

 

где радиус цилиндрической поверхности соприкосновения материалов, м.

2. В направлении оси z — как через плоскую стенку толщи­ной, равной расстоянию между узлами в этом направлении, и площадью F, равной площади кольца с радиусами , по формуле:

Аналогично изложенному учитываются и краевые условия, т. е. температуры для узлов, лежащих на поверхностях, грани­чащих с воздухом.

Лист

КР-2069059-270109-081405-2010

Если однородность поля нарушена около оси симметрии в пределах диаметра, равного 2 , то формула (38) оказывается непригодной для определения температур узлов, лежащих на оси симметрии. Если при этом температуры этих узлов опреде­лять из условий теплового баланса, то в знаменателе формулы (39) для количества тепла, отдаваемого от оси симметрии, по­лучим ln 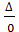,т. е. бесконечность, и Q = 0. В этом случае для оп­ределения величины Q приходится вводить некий условный диа­метр d₀, определяемый на основании следующих соображений.

Выделим около оси симметрии цилиндр диаметром 2 и та­кой же высоты (рис. 25). Количество тепла, передаваемого от узла с температурой , будет следующим:

а) в направлении радиуса к точкам с температурой :

б) в направлении оси z вверх к точке с температурой то :

в) в направлении оси z вверх к точке с температурой то :

Из условия теплового баланса или, под­ставляя их выражения и сокращая получим:

Решая полученное уравнение относительно , будем иметь:

C другой стороны, при однородном температурном поле для по формуле (38) имеем:

Приравнивая коэффициенты при

а) при

откуда

б) при

откуда

 

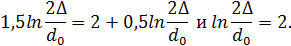
При

откуда .

КР-2069059-270109-081405-2010

Лист