Практическая работа
Тема: Вычисление площади и объема призмы, параллелепипеда и куба. (2 часа)
Цель работы: учиться вычислять площади и объемы призмы, параллелепипеда и куба.
В результате выполнения практической работы обучающийся должен
знать: формулы вычисления площадей и объемов призмы, параллелепипеда и куба.
уметь: уметь вычислять площади и объемы призмы, параллелепипеда и куба.
Форма проведения работы: практикум.
Используемое оборудование и инструменты: модели прямоугольного параллелепипеда, призм, линейки, карандаши, калькулятор.
Дополнительные материалы: краткий терминологический словарь.
Краткие теоретические сведения
Призма — многогранник, две грани которого являются многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
Многогранники
Таблица1
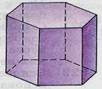
| Призма
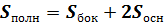 V
V 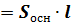 Прямая призма
Прямая призма
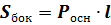 (l=h) (l=h)
| 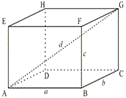
| Параллелепипед
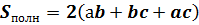 V=abc
V=abc
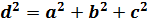
|
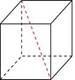
| Куб
 V=
V= 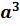
| Обозначения:
V - объем;
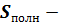 площадь полной поверхности; площадь полной поверхности;
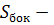 площадь боковой поверхности; площадь боковой поверхности;
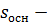 площадь основания; площадь основания; 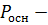 периметр основания;
l периметр основания;
l 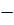 длина ребра; длина ребра; 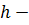 высота. высота.
|
Площади плоских многоугольников
Таблица 2
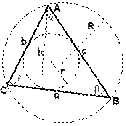
| Треугольник
S 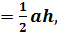 S
S  absinC
Формула Герона absinC
Формула Герона
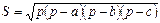 ,
где p= ,
где p= 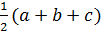 S =
S = 
| 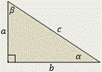
| Прямоугольный треугольник
S 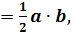 где a, b - катеты
где a, b - катеты
| ||||

| Квадрат
S 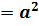
| ||||||

| Прямоугольник S = a · b | 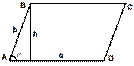
| Параллелограм S = a · h S = a · b · sin α | ||||
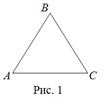
| Равносторонний треугольник
S 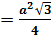
| 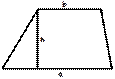
| Трапеция
| ||||
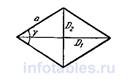
| Ромб
 D1, D2 – диагонали ромба
D1, D2 – диагонали ромба
| 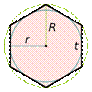
| Правильный шестиугольник
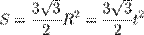
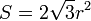
|
Рассмотрим пример нахождения площади боковой и полной поверхности призмы.
Инструкция:
1.Для нахождения площади боковой поверхности призмы нужно измерить линейкой следующие элементы призмы: стороны основания, высоту. Подставить значения в формулу для нахождения площади (если призма прямая) 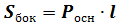 (l=h)
(l=h)
l 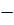 длина ребра;
длина ребра; 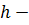 высота.
высота.
2. Для нахождения площади полной поверхности призмы нужно найти площадь основания призмы (площадь треугольника, прямоугольника, ромба)
Площадь полной поверхности призмы находиться как сумма площадей боковой поверхности и двух оснований.
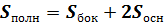 .
.
3. Объем вычисляется по формуле V 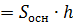
Оформление работы:
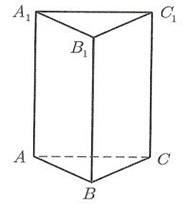
| Дано: АВСС1В1А1 треугольная призма, прямая, правильная
АВ=ВС=АС = 5 см, Н = 10 см
Найти: Sб.п., Sп.п., V.
Решение: Sб.п. = P•H
Р=5+5+5=15, Н=10
Sб.п.= 15•10 = 150 (см2)
Фо́рмула Герона позволяет вычислить площадь треугольника (S) по его сторонам a, в, c:
Sосн =  где p — полупериметр треугольника: р = (а+в+с):2
р= 15:2 =7,5
Sосн.=
где p — полупериметр треугольника: р = (а+в+с):2
р= 15:2 =7,5
Sосн.= 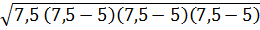 = = 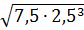 = = 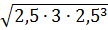 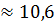 Sп.п. = P•H +2• Sосн, = 150 + 2 Sп.п. = P•H +2• Sосн, = 150 + 2 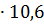 = 171,2 (см2)
V = 171,2 (см2)
V 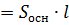 ?
V ?
V 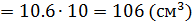 .
Ответ: Sб.п.= 150см2; Sп.п.=171,2см2;V .
Ответ: Sб.п.= 150см2; Sп.п.=171,2см2;V 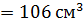 . .
|
| Порядок проведения работы (инструктаж): 1. Запишите в тетради тему занятия. 2. Внимательно прочитайте краткие теоретические сведения и выполните соответствующие записи в тетради. Разберите примеры. 3. Выполните в тетради задания на практическую работу. Записи в тетради должны содержать номер задания, формулировку задания и подробное решение. Содержание отчета: Тема занятия, краткие теоретические сведения, выполненные практические задания. Задание для практической работы 1.Вычислить площади боковой, полной поверхности и объем призмы по моделям (придумайте сами размеры 3-х моделей призм 3-4-6 угольных) (по образцу приведенному выше: чертеж, дано, найти, решение). Формулу для вычисления основания многогранника берем из таблицы 2. |
2. Задача. Коллекционер заказал аквариум, имеющий форму правильной четырехугольной призмы. Сколько квадратных метров стекла необходимо для изготовления аквариума, если сторона основания 70 см, а высота 60 см?