Спектральные характеристики непериодических сигналов

Задача 2.2.1. Построить спектры амплитуд и фаз сигнала U(t) на выходе генератора линейно изменяющегося напряжения (ГЛИН) при исходных данных: скорость изменения V_m:=4 volt∙Sec^-1 и длительность τ:=2 Sec.

Аналитическое выражение сигнала

Рисунок 15 – Сигнал U(t)

Ответ. Амплитудный спектр

 

Фазовый спектр

Задача 2.2.2. Найти спектр косинусоидальной функции y(t), заданной на интервале -τ/2 ≤t≤ τ/2 показанной на рисунке 16, при исходных данных: амплитуда U_m:= 0.5, длительность τ:= 0.2, при N:= 8 частота f₀:= N/τ или ω₀:= 2 ∙ π ∙ f₀, возможная периодичность повторения T:= 2 ∙ τ.

Аналитическое выражение функции

 

Рисунок 16 – Сигнал y(t)

Ответ. Спектр функции y(t)

Задача 2.2.3. Найти амплитудный спектр одиночного видеоимпульса S(t) синусоидальной формы при исходных данных: амплитуда U_m:= 2 volt; длительность τ:= 10 ^-1sec; при N:= 2 частота f₀:= 1/ (N∙τ) (угловая частота ω₀:= 2 ∙ π ∙ f₀) и период T₀:= N∙τ.

Аналитическое выражение сигнала:

Рисунок 17 – Видеоимпульс S(t)

Ответ. Амплитудный спектр

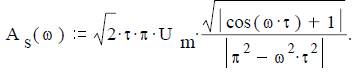
График амплитудного спектра видеоимпульса S(t) синусоидальной формы приведен на рисунке 18 при изменении угловой частоты ω в долях несущей частоты ω₀:= 2π/Т₀ в случае периодического продолжения импульсного сигнала с периодом T₀, а именно при

Рисунок 18 – График амплитудного спектра видеоимпульса S(t)

 

Задача 2.2.4. Решить задачу 2.2.3 с использованием теоремы о временном сдвиге.

Ответ. Амплитудный спектр

Задача 2.2.5. Найти спектры амплитуд и фаз экспоненциального видеоимпульса E(t), t≥0 sec с амплитудой U_m:= 1volt и коэффициентом затухания α:=0.1 sec^-1.

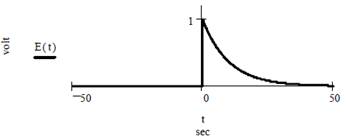
Рисунок 19 – Видеоимпульс E(t)

 

Математическая модель сигнала

Ответ. Амплитудный спектр

Фазовый спектр

Задача 2.2.6. Найти амплитудный спектр экспоненциального радиоимпульса E1(t), t≥0 sec (рисунок 20) с параметрами: амплитуда U_m:= 5volt; коэффициент затухания α:= 400 sec^-1; частота f₀:= 1000 Hz (ω₀:= 2πf₀).

Рисунок 20 – Экспоненциальный радиоимпульс E1(t)

 

Математическая модель сигнала

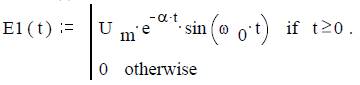
Ответ. Амплитудный спектр экспоненциального радиоимпульса

 

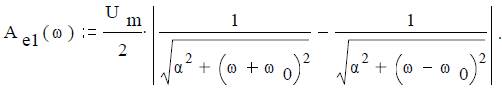
График амплитудного спектра приведен на рисунке 21 при

 

 

и изменении угловой частоты

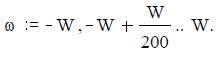
Рисунок 21 – График амплитудного спектра

 

Задача 2.2.7. Найти в рамках Mathcad спектры некоторых специальных функций:

1) дельта-функция δ (t) или функция Дирака

2) единичный скачок d(t) или функция Хевисайда

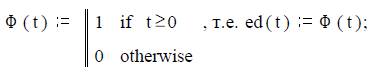
3) комплексная синусоида (пусть ω₀:= 5)

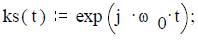
4) постоянная функция p(t):= A

ПРИМЕЧАНИЕ. Все эти функции абсолютно не интегрируемы, но путем предельного перехода для них можно найти интегральное преобразование Фурье.

Ответ. Спектральные функции:

ПРИМЕЧАНИЕ. Если интеграл непосредственно не берется, то следует использовать в Mathcad команды прямого преобразования Фурье «Fourier Transform» и обратного преобразования Фурье «Inverse Fourier Transform» меню Symbolic и Transforms.

Задача 2.2.8. Амплитудный спектр сигнала S(t) имеет параметры:

а) плотность амплитуд H:= 0.5 volt∙sec;

б) частоты среза спектра ω_c1:= 4 sec^-1 и ω_c2:= 3 ω_c1.

Амплитудный спектр описывается выражением

 

Спектр фаз равен нулю. Требуется найти вид сигнала S(t). График частотной характеристики (амплитудного спектра) приведен на рисунке 22 при W:=18 sec^-1 и ω:= -W, -W + W/200.. W.

Рисунок 22 – График частотной характеристики

Ответ. Сигнал

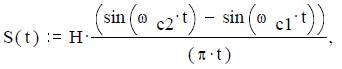
причем при t:=0 имеем

График сигнала при T:= 5sec и t:= 1.0 ∙ T, - 1.0 ∙ T + T/400.. 1.0 ∙ T приведен на рисунке 23.

Рисунок 23 – График сигнала