Методические указания к лабораторной работе
ХАРАКТЕРИСТИКИ ДЕТЕРМИНИРОВАННЫХСИГНАЛОВ
Дисциплина « Элементы общей теории сигналов »
СОГЛАСОВАНО РАЗРАБОТАЛИ
Инженер по охране труда Доцент кафедры ЭАПП
___________ Г.В. Мангуткина ________ А.С. Хисматуллин
____________2014 _____________2014
студент гр. БАТ-11-21
_________Е.И.Буланкин
_____________2014
Салават
Методические указания предназначены для студентов направления подготовки 220700 «Автоматизация технологических процессов и производств», профиль «Автоматизация технологических процессов и производств в нефтехимии и нефтепереработке»
Обсуждено на заседании кафедры ЭАПП
Протокол № ______ от ___________________2014
ã Филиал ФГБОУ ВПО УГНТУ в г.Салавате, 2014
ХАРАКТЕРИСТИКИ ДЕТЕРМИНИРОВАННЫХСИГНАЛОВ
Цель работы: изучение характеристик детерминированных сигналов
в программе «Mathcad».
Краткие теоретические сведения
Спектральные характеристики периодических сигналов
Условие периодичности – x (t) = x (t+mT), где T – период, m – натуральное число, m = 1, 2,.... Любой периодический сигнал x (t) может быть представлен тригонометрическим рядом Фурье.
x (t) = a0 + ∑ (ak cos kw1t + bk sin kw1t) = a0 + ∑ Ak cos(kw1t + φ k), (1.1)
где ω1 = 2π/T – угловая частота 1-й или основной гармоники; a0, аk, и bк коэффициенты разложения, вычисляемые по формулам:
a0 = 
ak = 
bk = 
где Ak – амплитуда k-й гармоники; φ k – фаза k-й гармоники; a0 – среднее значение сигнала (постоянная составляющая); k ω 1 = ω k – угловая частота k -й гармоники; tн – момент времени, соответствующий началу периода.
Зависимости Ak и φ k от частоты ω k – это спектры амплитуд и фаз соответственно.
В некоторых случаях более удобна комплексная форма ряда Фурье
(1.2)
Коэффициенты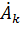 
ряда (1.2) вычисляются по формуле
(1.3)
Формулы (1.2) и (1.3) – пара преобразований Фурье. Совокупность коэффициентов 
комплексный спектр периодического сигнала x(t). Совокупность действительных величин 
в зависимости от частоты – спектр амплитуд. Совокупность величин φ k в зависимости от частоты – спектр фаз.
Ряд (1.2) удобно представлять в форме
(1.4)
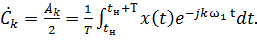(1.5)
Пример 1.1
Построить спектры амплитуд и фаз сигнала x(t), аналитическое выражение которого при исходных данных Vm:= 4volt∙sec-1,T:= 2 sec и t0:= 2 sec имеет вид
.
График сигнала при диапазоне изменения времени t:=-1.5∙T,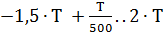 
представлен на рисунке 1.
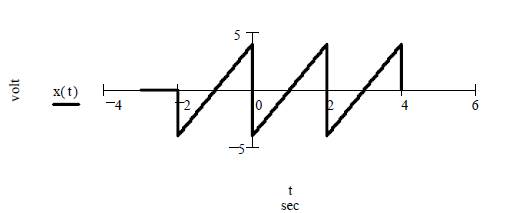
Рисунок 1 – График сигнала
Решение
Так как данный сигнал – периодическая функция времени, то для его спектрального представления нужно использовать или тригонометрический или комплексный ряд Фурье. Найдем спектры амплитуд и фаз на основе тригонометрического ряда Фурье.
Определим коэффициенты разложения сигнала на интервале t:= 0..T при угловой частоте основной гармоники ω1:= 
и числе гармоник k:= 1..5.
1) Постоянная составляющая
2) Косинусоидальный коэффициент
Подстановка численных значений Vm, T и ω1 дает
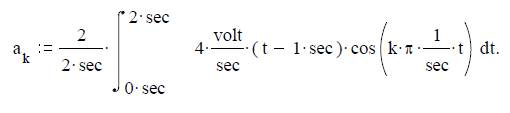
В результате интегрирования получим
Например, a1 = 0 volt; a2 = 0 volt; a3 = 0 volt; a4 = 0 volt.
Более удобна другая форма определения коэффициентов разложения.
Так как
то выражая t0 и ω1 через T, имеем
Отсюда следует, что при k>0 коэффициенты ak равны нулю.
3) Cинусоидальный коэффициент
Выражая t0 и ω1 через T, можно получить
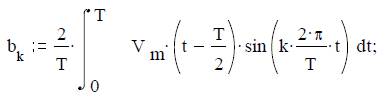
Отсюда после упрощений следует
Амплитуда k-й гармоники
при k>1 будет
Таким образом, с учетом постоянной составляющей амплитудный спектр
Фазовый спектр
Так как коэффициенты ak=0 и bk<0, и составит, например для k=1, φ = 1.571.
Графики данных спектров в виде столбчатых диаграмм приведены на рисунке 2.
Спектральные характеристики непериодических сигналов
Спектральное представление можно обобщить на случай, когда функция x (t) – непериодическая, т.е. T →∞. В этом случае применяется интегральное преобразование Фурье
(1.6)
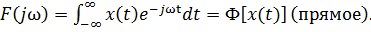(1.7)
Здесь Ф и Ф-1 – обозначения прямого и обратного оператора Фурье.
Формулы (1.6) и (1.7) – пара интегральных преобразований Фурье. Функция F (j ω) называется спектральной функцией или комплексным спектром непериодического сигнала. Она определена при положительных и отрицательных частотах.
Спектральную функцию можно представить в виде
, (1.8)
где 
– спектр амплитуд,
– спектр фаз.
Пример 1.2
Найти спектр функции x(t), заданной на интервале -τ/2<t<τ/2, при исходных данных: Um:= 0.5; τ:=2; возможная периодичность повторения T:= 2 ∙ τ (рисунок 3).
Аналитическое выражение функции
Рисунок 3 – Периодичность повторения
Решение
Поскольку функция представляет собой непериодическую функцию времени, найдем ее спектральную функцию (комплексный спектр) на основании интегрального преобразования Фурье (1.7). Оперируя безразмерными величинами, следует помнить, что спектральная функция характеризует спектральную плотность амплитуд и фаз элементарных комплексных гармонических колебаний 
. Она имеет для сигнала в виде напряжения размерность вольт × секунда. Угловая частота ω имеет размерность радиан/секунда.
Так как заданная функция является четной, то ее спектр должен быть вещественной функцией. Для представления вещественной функции достаточен один график.
Интегральное преобразование Фурье
Интегрирование дает действительную функцию
Полученное выражение запишем в компактной форме, введя определение функции отсчетов
Тогда, умножая числитель и знаменатель спектральной функции на τ/2, ее можно записать в виде
Эта спектральная функция при ω:=0 имеет неопределенность вида 0/0. Раскроем неопределенность по правилу Лопиталя
График спектральной функции приведен на рисунке 4 при T:= 2∙τ, изменении угловой частоты ω с шагом в долях частоты первой гармоники ω1:= 2∙π/Т и числе гармоник R:= 12 (в случае периодического продолжения), а именно при ω:= -R∙ ω1, -R∙ ω1 + ω1/100.. R∙ ω1.
Рисунок 4 – График спектральной функции
Амплитудный спектр определяется как модуль спектральной функции
Переход от действительной и знакопеременной спектральной функции Fx(ω) к амплитудному спектру Ax(ω) требует введения фазового спектра. При взятии модуля спектральная функция изменяет фазу на 1800 = π (при M:= 4 и k:= 1.. M) в точках ωk:= (2k)∙π/ τ, когда значения Sa(ωτ/2)<0.
Таким образом, фазовый спектр
Графики амплитудного и фазового спектров приведены на рисунках 5 и 6.
Рисунок 5 – Амплитудный спектр
Рисунок 6 – Фазовый спектр
Отсюда следует спектральная функция в экспоненциальной форме.
Рисунок 7 – Спектральная функция в экспоненциальной форме