Решение большинства задач теории автоматического управления, основано на использовании математических моделей исследуемых систем. Математические модели систем обычно составляются из математических моделей её составных частей (звеньев).
Схема системы, представленная в виде совокупности (соединения) всех её элементов представленных передаточными функциями, называется структурной схемой системы.
В состав структурных схем входят:
1) линии связи со стрелками, указывающими направление передачи сигнала;
 |
2) узлы суммирования и вычитания (сравнения);
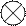
 x + y = x+x1 x y = x+x1
x + y = x+x1 x y = x+x1

 +
+
x1 x1
зачерненный сектор или знак (-) указывает на инверсию входного сигнала;
3) точки съема сигнала или точки разветвления:
 x x
x x
 x
x
Пример, структурной схемы линейной непрерывной системы:
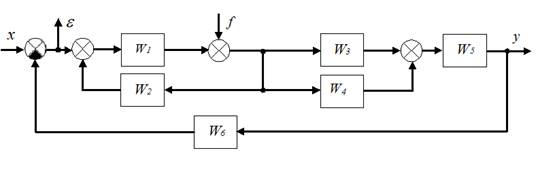
На приведенной схеме стрелками с буквами показаны входные и выходные сигналы относительно которых, можно получить передаточные функции исходной системы.
Например: 
|

2) Wfy -?
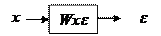 |
3) Wx 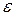 -?
-?
 4) Wf
4) Wf 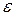 -?
-?
Указанные передаточные функции системы позволяют установить математические зависимости между соответствующими входными и выходными сигналами.
|
1) Объединение последовательно соединенных звеньев:
 |



 x y
x y
 x y Wэкв =
x y Wэкв = 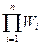
2) Объединение параллельно соединённых звеньев:
 | |||
 | |||
Wэкв = 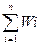
3) Замыкание звена обратной связью:
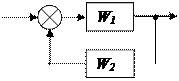 x y
x y
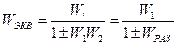


 |
«+» - при отрицательной обратной связи
«–» - при положительной обратной связи
4) Приведение ОС к единичной:
|
|
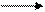
|

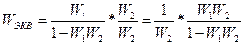
 | |||
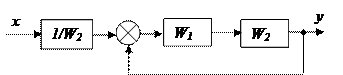 | |||
5) перенос точки съёма через линейное звено против хода сигнала:
| |||||
|  | ||||

|

|
 | |||||||
 | |||||||
 | |||||||
|
|
|
6) перенос точки съёма через линейное звено по ходу сигнала: 
|

|
|
|
 x y x
x y x
 |  | ||||
 | |||||
|
|
 x
x
 |
|
| |||||||
| |||||||
| |||||||
| |||||||



 x
x
 | |||||||
| |||||||
 | |||||||
 | |||||||
y = x·W + x1 y= (x+x1·1/W)·W = xW + x1
8) Перенос сумматора через линейное звено по ходу сигнала:
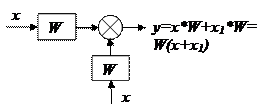 | |||||
 | |||||
 | |||||
Пример №1 преобразования структурных схем.
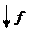 |
|
|
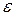 y
y





 |

Требуется определить следующие передаточные функции линейной системы:

|

2) Wfy -?
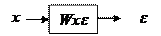 |
3) Wx 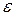 -?
-?
 4) Wf
4) Wf 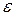 -?
-?
Заданная система линейна, значит, для неё справедлив принцип суперпозиции, что позволяет при выполнении преобразований не учитывать входные и выходные сигналы, не задействованные при определении конкретных передаточных функций.
Так при определении передаточной функции Wху отбрасывается возмущающее воздействие f и не учитывается 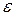 и по выше рассмотренным правилам выполняются следующие упрощения (преобразования) структурной схемы и вводятся новые обозначения:
и по выше рассмотренным правилам выполняются следующие упрощения (преобразования) структурной схемы и вводятся новые обозначения:
W6 = W1 + W2 – объединение параллельно соединенных звеньев W1 и W2,
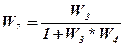 – эквивалентная передаточная функция звена W3, охваченного отрицательной обратной связью содержащей звено W4.
– эквивалентная передаточная функция звена W3, охваченного отрицательной обратной связью содержащей звено W4.
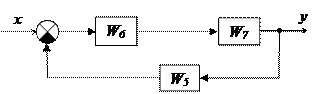 |
W8 = W6·W7 – объединение
последовательно соединенных звеньев W6 и W7
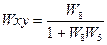 . После подстановки обозначений передаточных функций элементов исходной системы получим:
. После подстановки обозначений передаточных функций элементов исходной системы получим:
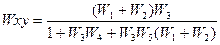 – передаточная функция, определяющая зависимость (связь) выходной величины Y от входной X.
– передаточная функция, определяющая зависимость (связь) выходной величины Y от входной X.
Аналогично определяются другие передаточные функции системы.
Пример №2 преобразования структурных схем.
Задана структурная схема:
 |
Требуется получить эквивалентную передаточную функцию Wxy.
1. Объединяем в одно два последовательно соединенных звена:
W5 = W1*W2.
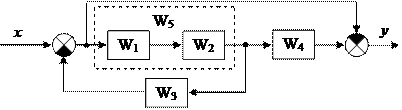 |
2. Для дальнейшего упрощения структурной схемы необходимо из контура с обратной связью (W5 , W3 , сумматор) удалить точку съема (разветвления) сигнала, иначе к данному контуру нельзя применить правило охвата звена обратной связью. Для того чтобы, после переноса точки съема сигнал на входе второго сумматора остался неизменным, в цепь этого сигнала добавляем звено с передаточной функцией обратной W5.
 | |||
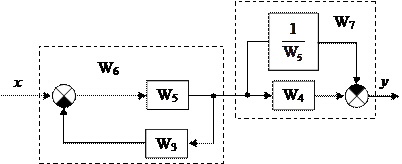 |
3. Долее по правилам преобразования звена охваченного обратной отрицательной связью получаем:
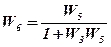 и для параллельного соединения
и для параллельного соединения 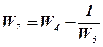 .
.
 |
4. В итоге имеем: 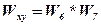 .
.
После подстановки в полученное выражение обозначений передаточных функций звеньев исходной схемы и упрощения выражения получим:
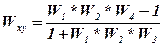
Пример №3 преобразования структурных схем.
Задана структурная схема:
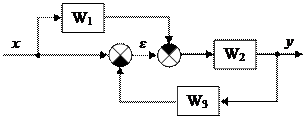 |
Требуется определить передаточные функции Wxy и W xε.
При определении передаточной функции Wxy достаточно сумматоры поменять местами (переставить) и применить правила преобразования структурных схем для параллельного соединения звеньев, звена охваченного отрицательной обратной связью и последовательного соединения:
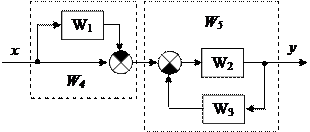 |
 ;
; 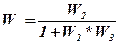 ;
; 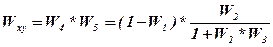
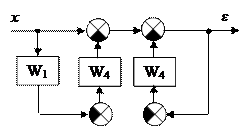
При определении передаточной функции W xε исходную схему следует преобразовать к виду:
 |
Для этого отбрасываем выходную величину y и поэтапно упрощаем схему:
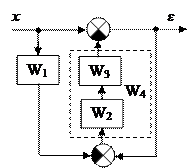 | |||
 | |||
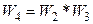
 | |||
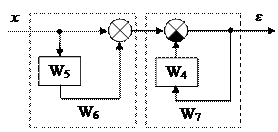 | |||
Теперь имеем:
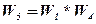
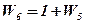 ;
; 
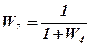 ;
; 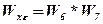 .
.
Далее необходимо в полученном выражении W xε сделать подстановку исходных обозначений передаточных функций использованных в первоначальной структурной схеме.
