Контрольная работа по темам «Теория вероятностей и математическая статистика»
ФИО,
Гр. ЗФ-
Вариант (по списку группы)
m=, n= (свои у каждого)
| Вариант | m | n |
А.С.Шапкин, В.А. Шапкин «Задачи с решениями по ВМ, ТВ,МС и МП»
Вариант кр по списку группы, у каждого свои значения m и n, решить шесть обязательных задач
На «удовлетворительно» необходимо набрать 60 баллов
(9 занятий*3=27 баллов (без пропусков: +3 балла=27+3=30),
6 задач*5 баллов=30 баллов)
На «хорошо» необходимо набрать 75 баллов
(каждую задачу сопровождать указанием на метод и теорему, используемые при решении и обьяснением какая переменная что обозначает, написать формулировку теоремы и выделить красным цветом, 6 задач*2,5 балла=15 баллов)(или решить 3 дополнительные задачи 3*5=15 баллов)
На «отлично» необходимо набрать 90 и выше баллов
(при письменном экзамене и дистанционной беседе, сообщить о своем намерении за сутки до экзамена).
Окончательный срок сдачи задач за двое суток до даты экзамена.
Индивидуальные обязательные задачи (ИДЗ или КР)
12. Теория вероятностей
12.1. Случайные события
12.1.1.(кр, задача 1) В ящике находятся (m + 3) одинаковых пар перчаток черного цвета и (n + 2) одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.
12.1.2. (кр, задача 2) В урне находятся 3 шара белого цвета и (n + 1) шаров черного цвета. Наудачу по одному извлекаются 3 шара и после каждого извлечения возвращаются в урну. Найти вероятность того, что среди извлеченных шаров окажется:
а) ровно два белых шара;
б) не менее двух белых шаров.
12.1.3. (кр, задача 3) В урне находятся (m + 2) белых (n + 2) черных шара. Последовательно извлекаются наудачу три шара без их возвращения в урну. Найти вероятность того, что третий по счету шар окажется белым.
12.2. Случайные величины
12.2.1. (кр, задача 4) Закон распределения дискретной случайной величины x имеет вид:
| pi | -2 | -1 | m | m+n | |
| Pi | -0,2 | -0,1 | 0,2 | P4 | P5 |
Найти вероятности p4, p5, и дисперсию D (X), если математическое ожидание М (Х) = –0,5 + 0,5m + 0,1n.
13. Математическая статистика
13.1. (кр, задача 5 а) Численная обработка данных одномерной выборки
Выборка Х объемом N = 100 измерений задана таблицей:
| Xi | X1 | X2 | X3 | X4 | X5 | X6 | X7 |
| mxi | 20+(m+n) | 30-(m+n) |
где xi — результаты измерений, mxi — частоты, с которыми встречаются значения xi,
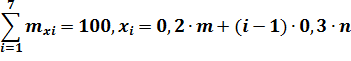
13.1.1. (кр,задача 5 а) Построить полигон относительных частот Wi=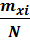 
13.1.2. (кр, задача 5 б) Вычислить среднее выборочное 
, выборочную дисперсию Dx и среднее квадратическое отклонение σ х.
Пример оформления ИДЗ или КР (можно как в учебнике)
Задача 1. (Шапкин 12.1.1.)
В ящике находятся (m+3)= одинаковых пар перчаток черного цвета и (n+2) = одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченных перчатки образуют пару.
Решение:
Пусть А – случайное событие, что извлечена черная пара; В – случайное событие, что извлечена бежевая пара.
Тогда событие С=А+В – извлеченные из ящика две перчатки одного цвета и образуют пару. А и В – несовместные события. Р(С)=Р(А)+Р(В) – формула сложения для несовместимых событий.
Вероятности Р(А) и Р(В) вычислим по формуле классического определения вероятности:
1) 
, где 
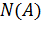-число благоприятных исходов события А, т.к. (m+3)= левых и (m+3)= правых черного цвета, то 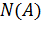= (m+3)∙ (m+3)=.
Всего перчаток ((m+3)+ (n+2))∙2= 2m+2n+10=,
Общее число исходов 
,
получим Р(А)=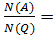 
2) 
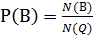, где 
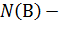число благоприятных исходов событию В, т.к. (n+2) = левых и (n+2) = правых бежевого цвета, то 
= (n+2) ∙(n+2) =.
Всего перчаток ((m+3)+ (n+2))∙2= 2m+2n+10=,
Общее число исходов ,
получим Р(В)= 
Тогда Р(С)=Р(А)+Р(В)= 
Ответ:
Задача 2. (Шапкин 12.1.2.)
В урне находятся 3 шара белого цвета и (n+1) = шаров черного цвета. Наудачу по одному шару извлекают 3 шара и после каждого извлечение возвращаются в урну. Найти вероятность того, что среди извлеченных шаров окажется:
а) ровно 2 белых шара;
б) не менее двух белых шаров.
Решение: Проводятся многократные испытания.
n=3 (число испытаний по извлечению шаров),
Событие B - извлекается шар белого цвета, его вероятность в каждом испытании постоянна и равна
p=Р(В)=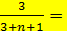 
, (вычисляется по классической формуле).
Вероятность взять черный шар: q=1-p=.
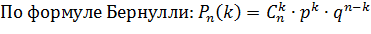
а) вероятность того,что среди излеченных шаров ровно 2 белых шара
k=2 p= 
, q=
б) вероятность того, что из трех извлеченных шаров окажется не менее двух (т.е. два или три)
Р3(k≥2)=P3(2)+P3(3)= 
Ответ: а); б).
Задача 3. (Шапкин 12.1.3.)
В урне находятся (m+2)= белых, (n+2)= черных шара. Последовательно извлекаются наудачу три шара без их возвращения в урну. Найти вероятность того, что третий по счету шар окажется белым.
Решение:
Пусть А – случайное событие, что третий по счету извлеченный шар белый. Это событие можно представить как сумму четырех несовместных событий:
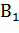– первый шар белый.
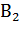– второй шар белый.
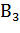– третий шар белый.
Перечислим возможные события:
.
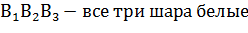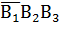– первый шар черный; второй и третий белые
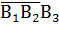– первый и второй черные; третий белый
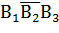– первый и третий белые; второй черный
По формуле несовместных событий:
В каждом слагаемом события между собой зависимы, так как шары после извлечения в урну не возвращаются. По условию в урне 6 белых и 5 черных шаров. Будем использовать классическое определение вероятности и теорему умножения для зависимых событий:
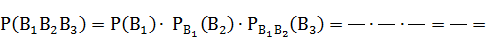
Аналогично рассуждая, получим:
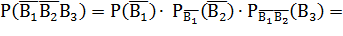
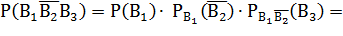
Искомая вероятность
Ответ: 
Задача 4. (Шапкин 12.2.1.)
Закон распределения дискретной случайности величины Х имеет вид
| xi | -2 | -1 | m | m+n | |
| рi | 0,2 | 0,1 | 0,2 | р4 | р5 |
Найти вероятности р4, р5 и дисперсию D(X), если математическое ожидание М(X)=-0,5+0,5∙m+0,1∙n=
Решение:
М(X)= x1∙ р1+ x2∙ р2+ x3∙ р3+ x4∙ р4+ x5∙ р5=
0,2+0,1+0,2+ р4+р5=1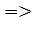 
0,5+ р4+р5=1 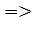р4+р5=0,5
Решим систему из двух уравнений с двумя неизвестными
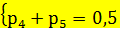
р5=1
р4=
р4=
М(
)= (-2)2∙0,2+(-1)2∙0,1+02∙0,2+m2∙ 0,4+(m+n)2∙ 0,1=0,8+0,1+0++=
D(X)= М()-[M(X)]2=
Ответ: р4=; р5=; D(X) =
Задача 5 а (Шапкин 13.1.1.)
5 б (Шапкин 13.1.2.)
Выборка Х объемом N=100 измерений задана таблицей
| xi | X1 | X2 | X3 | X4 | X5 | X6 | X7 |
| ni | 20+(m+n) | 30-(m+n) |
Где xi=0,2m+(i-1)*0.3*n – результат измерений.
ni частоты, с которыми встречаются xi
а) построить полигон относительных частот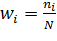 
б) вычислить среднее выборочное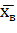 
, выборочную дисперсию 
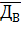, среднее квадратическое отклонение 
.
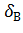m=, n=
Решение:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni |
Подставляем m=, n= в формулу xi=0,2m+(i-1)*0.3*n, меняя номер-индекс
=> x1=
x2=
x3=
x4=
x5=
x6=
x7=
Получим таблицу
| xi | |||||||
| ni |
б) среднее выборочное
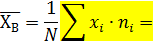
Выборочная дисперсия
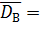
Среднее квадратическое отклонение
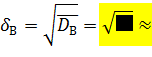
a) построить полигон относительных частот
Например: (соединяет отрезками прямой, не плавно). На осях наносим данные своей задачи. (свои цифры)
Дополнительные задания
12.2.2. Плотность распределения непрерывной случайной величины Х имеет вид:
Найти:
а) параметр а;
б) функцию распределения F (x);
в) вероятность попадания случайной величины X в интервал
;
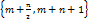г) математическое ожидание M (X) и дисперсию D (X).
Построить графики функций f (x) и F (х).
12.2.3. Случайные величины X1, X2, X3 имеют геометрическое, биномиальное и пуассоновское распределения соответственно. Найти вероятности P (m ≤ Xi ≤ m + 2), если математические ожидания М (Xi) = n + 1, а дисперсия D (X2) = (n + 1)(7 – n) / 8.
12.2.4. Случайные величины X4, X5, X6 имеют равномерное, показательное и нормальное распределения соответственно. Найти вероятности P (n < Xi < n + m), если у этих случайных величин математические ожидания и средние квадратические отклонения равны m.
13.1.3. По критерию χ 2 проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости α = 0,05.
Примечание. Для расчетов 
и Dx рекомендуется перейти к условным значениям Ui =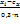 
и, взяв за ложный нуль сх значение с наибольшей частотой, использовать суммы
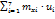и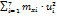 
13.2. Построение уравнения прямой регрессии
Двумерная выборка результатов совместных измерений признаков x и y объемом N = 100 измерений задана корреляционной таблицей:
| y1 | y2 | y3 | y4 | y5 | 
| |
| - | - | - | |||
| - | - | ||||
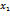
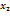
| - | 8+m | 12+n | - | - | 20+(m+n) |
| - | - | 16-m | 14-n | - | 30-(m+n) |
| - | - | - | |||
| - | - | ||||
| - | - | - | |||
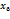
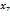
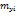
| 19+m | 42+n-m | 31-n | N=100 |
где xi = 0,2 · m + (i – 1) · 0,3 · n, yj = 0,5 · m + (j – 1) · 0,2 · n.
13.2.1. Найт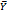и 
и 
y для выборки
| 
| 
| 
| 
| 
|
|
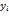
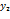
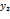
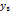
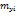
| 19+m | 42+n-m | 31-n |
(Расчеты 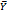и 
можно провести аналогично расчетам и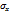 
в задаче 13.1.2).
13.2.2. Построить уравнение прямой регрессии Y на Х в виде 
x =ax+b, и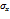 
следует взять из задачи 13.1.2.
13.2.3. На графике изобразить корреляционное поле, то есть нанести точки (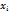
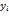, ) и построить прямую x=ax+b
Примечание. Уравнение регрессии сначала рекомендуется найти в виде 
,где r — выборочный коэффициент корреляции, для расчета которого можно воспользоваться методом четырех полей.