Вероятность того, что кофе останется в первом автомате равна 1 − 0,25 = 0,75. Вероятность того, что кофе останется во втором автомате равна 1 − 0,25 = 0,75. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,15 = 0,85. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,85 = 0,75 + 0,75 − х, откуда искомая вероятость х = 0,65.
Примечание.
Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,25·0,25 = 0,0625, однако, по условию, эта вероятность равна 0,15.
Задание 10 № 320176
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение. Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».
События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час, наносекунду и т. д. — равна нулю. Тогда:
P(A + B + С) = P(A) + P(B) + P(С)= P(A) + P(B),
откуда, используя данные из условия, получаем
0,97 = P(A) + 0,89.
Тем самым для искомой вероятности имеем:
P(A) = 0,97 − 0,89 = 0,08.
Ответ: 0,08.
Задание 10 № 509569
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение. Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».
События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:
P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B),
откуда, используя данные из условия, получаем
0,93 = P(A) + 0,87.
Тем самым, для искомой вероятности имеем:
P(A) = 0,93 − 0,87 = 0,06.
Ответ: 0,06.
Задание 10 № 509916
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17.
Решение. Рассмотрим события A = «в автобусе меньше 10 пассажиров» и В = «в автобусе от 10 до 17 пассажиров». Их сумма — событие A + B = «в автобусе меньше 18 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,82 = 0,51 + P(В), откуда P(В) = 0,82 − 0,51 = 0,31.
Ответ: 0,31.
Задание 10 № 320173
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение. Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна
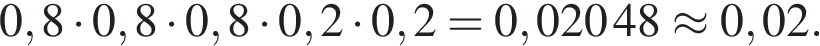
Ответ: 0,02.
Задание 10 № 320175
Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение. Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,3·0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.
Ответ: 0,91.
Задание 10 № 320187
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
В ответе укажите наименьшее необходимое количество выстрелов.
Решение. Найдем вероятность противоположного события, состоящего в том, что цель не будет уничтожена за n выстрелов. Вероятность промахнуться при первом выстреле равна 1 − 0,4 = 0,6, а при каждом следующем 1 − 0,6 = 0,4. Эти события независимые, вероятность их произведения равна произведению вероятности этих событий. Поэтому вероятность промахнуться при n выстрелах равна: 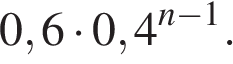
Осталось найти наименьшее натуральное решение неравенства
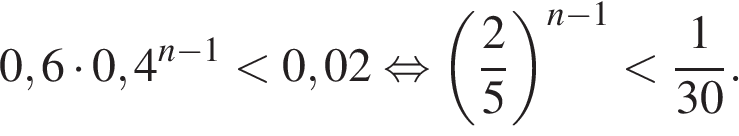
Последовательно проверяя значения n, равные 1, 2, 3 и т. д. находим, что искомым решением является  Следовательно, необходимо сделать 5 выстрелов.
Следовательно, необходимо сделать 5 выстрелов.
Ответ: 5.
Примечание.
Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов:
Р (1) = 0,6.
Р (2) = Р (1)·0,4 = 0,24.
Р (3) = Р (2)·0,4 = 0,096.
Р (4) = Р (3)·0,4 = 0,0384;
Р (5) = Р (4)·0,4 = 0,01536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени.