Параметром, характеризующим быстродействие рассматриваемых объектов, является суммарная постоянная времени 
. Этот параметр был введен многими авторами в начале 1960-х годов. Для системы с передаточной функцией:
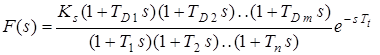
суммарная постоянная времени:
.
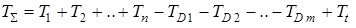Величина 
может быть получена и непосредственно из ответной реакции на ступенчатый входной сигнал системы. Для этого на кривой переходного процесса выбирают две точки с координатами 
и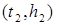 
(желательно в начале и в конце спрямленного участка, в центре которого находится точка перегиба). Далее вычисляют величины 
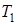и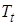 
по следующим формулам:
,
,
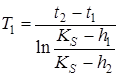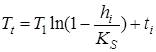где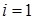 
или 2.
Суммарная постоянная времени равна:
.
Метод основан на аппроксимации объекта звеном третьего порядка вида:
,
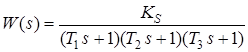где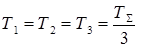 
.
Затем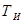 
и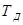 
выбирают таким образом, чтобы компенсировать два полюса. Приведем вывод формул для 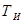и .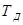
Передаточная функция прямого канала системы имеет вид:
,
.
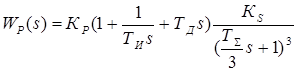Для компенсации двух полюсов необходимо соблюдение равенства:
.
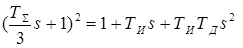Откуда
, (9)
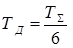. (10)
После компенсации двух полюсов передаточная функция замкнутой системы примет вид:
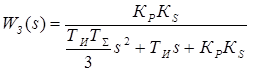. (11)
Коэффициент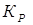 
выбирают таким, чтобы коэффициент демпфирования контура был равен 
. По мнению специалистов, такой коэффициент демпфирования дает оптимальную динамику системы в отношении времени переходного процесса и перерегулирования. После подстановки (9) и (10) в (11) получим формулу: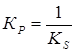 
.
Благодаря оптимизации по интегральной оценке качества регулирования, представляется возможность настройки регулятора для модели объекта второго порядка еще лучше, т.е. с большим быстродействием (табл. 1). Эти параметры дают хорошие результаты для объектов регулирования с моделью первого или второго порядка. Но для объектов более высокого порядка наблюдается заметное перерегулирование. Поэтому быстрая настройка применима тогда, когда известно, что объект соответствует звеньям первого или второго порядка. А нормальная («медленная, осторожная») настройка, напротив, почти всегда дает хорошие результаты для звеньев объекта более высокого порядка.
Таблица 1
| Вид настройки | Тип регулятора | Параметры регулятора | ||
| 
| 
| ||
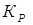
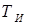
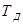
| Нормальная | П | 
| – | – |
| ПД |
| – | 
| |
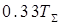
| ПИ | 
| 
| – | |
| ПИД |
| 
| 
| |
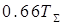
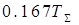
| Быстрая | ПИ |
| 
| – |
| ПИД |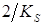 
| 
| 
|
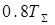
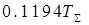
Метод настройки Шеделя
Метод основан на принципе каскадного коэффициента демпфирования. Шедель обобщает понятие коэффициента демпфирования на случай системы третьего порядка. Здесь для системы с передаточной функцией вида:
справедливы следующие выражения:
, 
.
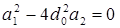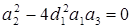Коэффициенты ПИД-регулятора настраивают так, чтобы коэффициенты демпфирования системы были равны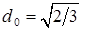 
, 
.
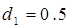В случае объекта вида:
совершается переход к следующей форме:
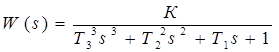, (12)
где
, 
, 
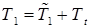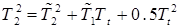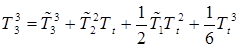. (13)
Параметры ПИД-регулятора рассчитываются по следующим формулам:
, 
и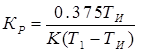 
. (14)
Метод Шеделя сокращает время переходного процесса, незначительно увеличивая перерегулирования (менее 10%).