3.1. Математическая корректность по Ж. Адамару.
Корректность задач математической физики рассмотрим на примере уравнения теплопроводности. Для теплофизических задач Y = Q – количество тепла, Дж; Y = Q – тепловой поток, Вт; Ф Y = T – температура, К; ξ Y = λ – теплопроводность, Вт/(м∙К)
Распространение тепла описывается дифференциальными уравнениями параболического типа в частных производных первого порядка по времени и второго порядка по пространственным координатам [5]:
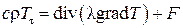 , ,
| (3.1) |
где T = T (x, y, z, τ) – температура; λ = λ(x, y, z, T) – теплопроводность; F = F (x, y, z, T, τ) – плотность тепловых источников. Если среда однородна, уравнение принимает вид
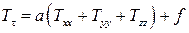 , ,
| (3.2) |
где a = λ / c ρ – температуропроводность, f = F / c ρ, или
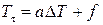 , ,
| (3.3) |
где Δ – оператор Лапласа.
Уравнения (3.1)-(3.3) в частных производных составляют основу математических моделей с распределенными параметрами. В случае пренебрежения пространственным распределением температуры уравнения становятся обыкновенными дифференциальными (ОДУ) и образуют модели с сосредоточенными параметрами:
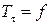 . .
| (3.4) |
При решении краевых задач доказываются две теоремы – существования и единственности решения. Если существование решения доказано, то по теореме о единственности решения функция T, удовлетворяющая в области определения уравнению (3.1), начальным и граничным условиям, единственна при выполнении в области определения следующих условий [5]:
1) функция T и ее производные, входящие в уравнение (3.1), непрерывны;
2) коэффициенты с, ρ, λ непрерывны;
3) краевых (граничных и начальных) условий достаточно.
В связи с физической обусловленностью задач математической физики используется понятие корректности. Математическая задача поставлена корректно, если [5]:
1) решение задачи существует;
2) задача имеет единственное решение;
3) решение непрерывно зависит от исходных данных (устойчиво).
Если одно или несколько условий не выполняются, задача математически некорректна. Следовательно, корректная постановка краевой задачи основана на физически обусловленной математической модели.
В общем случае разработка математической модели состоит из двух этапов – структурной и параметрической идентификации. Структурная идентификация заключается в определении общей структуры математической модели в виде тех или иных уравнений. Параметрическая идентификация предполагает наделение выбранной модели необходимой количественной информацией – определение неизвестных характеристик модели [6].
В случае тепловых процессов структурная идентификация заключается в выборе вида уравнения (3.1), параметрическая – в определении коэффициентов с, ρ, λ, F, которые могут являться функциями координат, времени (x, y, z, τ) и температуры T. При отсутствии справочной информации или недостаточной точности прямых методов расчета искомых параметров они восстанавливаются по температурному полю – решается коэффициентная обратная задача теплообмена [6].
Теорема о единственности решения содержит также требование достаточности количества начальных и граничных условий. Если условий недостаточно, они восстанавливаются решением граничной обратной задачи. По принятой классификации коэффициентные задачи называются задачами идентификации, граничные – задачами диагностики [6].
Нарушение причинно-следственных связей в обратных задачах теплообмена противоречит второму закону термодинамики в части необратимости теплового процесса и приводит к их некорректности, проявляющейся при математической формализации чаще всего в виде неустойчивости решения [6].
3.2. Устойчивость решения краевых задач на основе математических моделей с сосредоточенными параметрами.
Требование устойчивости решения обусловлено тем, что всякий физически определенный процесс, развивающийся во времени, должен характеризоваться функциями, непрерывно зависящими от краевых условий. При отсутствии непрерывной зависимости нарушается требование единственности решения, так как появляется множество функций, удовлетворяющих системе краевых условий [5].
Поскольку в дальнейшем речь пойдет о математических моделях с сосредоточенными параметрами, рассмотрим вопрос устойчивости решения системы обыкновенных дифференциальных уравнений (СОДУ) на основе уравнения (3.4) [7]:
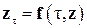 . .
| (3.5) |
В краевой постановке неизвестной является N -мерная вектор-функция z с компонентами T 1,…, TN. Для ее определения достаточно начального условия [7]
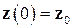 . .
| (3.6) |
Далее приводятся два определения устойчивости решения системы (3.5), (3.6) по Ляпунову [7]:
1) решение z = z (τ, z 0) задачи (3.5), (3.6) устойчиво, если для любого ε > 0 существует δ(ε) такое, что при ||Δ z 0|| < δ(ε) для всех τ > 0 справедливо неравенство
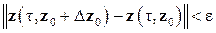 ; ;
| (3.7) |
2) решение z = z (τ, z 0) задачи (3.5), (3.6) асимптотически устойчиво, если оно устойчиво и существует такое достаточно малое δ0 > 0, что при ||Δ z 0|| < δ0
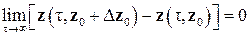 . .
| (3.8) |
Исследование на устойчивость решения z = z (τ, z 0) можно свести к исследованию на устойчивость тривиального решения
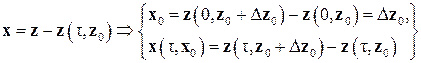 . .
| (3.9) |
Тогда система (3.5) примет вид [7]
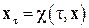 , ,
| (3.10) |
где χ (τ, x) = f (τ, x + z (τ, z 0)) – z τ(τ, z 0).
Далее приводятся два определения устойчивости решения системы (3.10) по Ляпунову [7]:
1) тривиальное решение x ≡ 0 системы (3.10) устойчиво, если для любого ε > 0 существует δ(ε) такое, что при || x 0|| < δ(ε) для всех τ > 0 справедливо неравенство
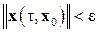 ; ;
| (3.11) |
2) тривиальное решение x ≡ 0 системы (3.10) асимптотически устойчиво, если оно устойчиво и существует такое δ0 > 0, что при || x 0|| < δ0
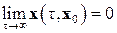 . .
| (3.12) |
В случае, когда χ не зависит явно от τ, система (3.10) в координатной форме принимает вид [7]:
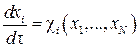  . .
| (3.13) |
Так как понятие устойчивости тривиального решения связано с малой окрестностью начала координат в фазовом пространстве, предполагается, что поведение решения системы (3.13) при разложении функций χi в ряд Тейлора будет определяться членами первого приближения. Тогда по формуле Тейлора, учитывая, что χi(0,…,0) = 0, и пренебрегая членами ряда с производными второго порядка, получаем так называемую систему первого приближения для системы (3.13) [7]
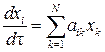 , ,
| (3.14) |
или в матричном виде
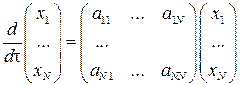 , ,
| (3.15) |
где aik = ∂χ i (0,…,0) / ∂ xk – элементы матрицы членов первого приближения (i = 1,…, N; k = 1,…, N). Данная система является редуцированным случаем более общей задачи
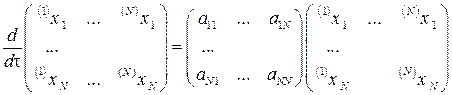
| (3.16) |
или
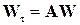 , ,
| (3.17) |
в которой неизвестной является фундаментальная матрица W, состоящая из N столбцов
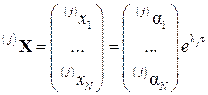  . .
| (3.18) |
где λ j – характеристические числа матрицы А, определяемые как корни характеристического уравнения
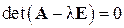 , ,
| (3.19) |
(j)α i – некоторые числа, если λ1 ≠ λ2 ≠ … ≠ λ N, и многочлены по τ, если λ1 = λ2 = … = λ N.
Для системы (3.16), и, в частности, (3.15), доказывается теорема, позволяющая судить об устойчивости тривиального решения по характеристическим числам матрицы первого приближения.
Пусть в некоторой окрестности точки x 1 = 0, …, xN = 0 функции χ i (x 1,…, xN) (i = 1,…, N) непрерывны вместе с производными до второго порядка включительно. Тогда, если все характеристические числа λ i матрицы с элементами aik удовлетворяют условию Re λ i < 0, то тривиальное решение системы (3.16), и, в частности, (3.15), устойчиво и притом асимптотически. Если же Re λ i > 0 хотя бы для одного i, то тривиальное решение системы неустойчиво [7].
Таким образом, устойчивость решения краевых задач полностью определяется характером функций в правой части уравнений системы (3.5).
Лекция III
3.3. Корректность решения задач идентификации математических моделей с сосредоточенными параметрами.
Рассмотрим поведение решения системы (3.5),  при разложении функций fi в ряд Тейлора в окрестности гипотетической точки (0,…,0) по членам первого приближения. Пренебрегая членами ряда с производными второго порядка и учитывая, что вблизи абсолютного нуля решение системы (3.5) стремится к тривиальному, т. е. fi (0,…,0) = 0, получаем гипотетическую систему первого приближения
при разложении функций fi в ряд Тейлора в окрестности гипотетической точки (0,…,0) по членам первого приближения. Пренебрегая членами ряда с производными второго порядка и учитывая, что вблизи абсолютного нуля решение системы (3.5) стремится к тривиальному, т. е. fi (0,…,0) = 0, получаем гипотетическую систему первого приближения
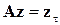 . .
| (3.20) |
где A = [ aik (τ)]= ∂ fi (τ; 0,…,0) / ∂ Tk (τ) (i = 1, 2, …, N; k = 1, 2, …, N); z = [ T 1(τ), …, TN (τ)]T. Перейдём от системы обыкновенных дифференциальных уравнений к системе линейных алгебраических уравнений (СЛАУ) экспериментальным определением температур:
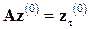 , ,
| (3.21) |
где z (0) = (T 1(0), …, TN (0))T – экспериментально определенный вектор температур.
Решение задачи идентификации матрицы A неединственно, т. к. количество N 2 функций матрицы A больше количества N уравнений в системе (3.21). Поэтому для восстановления условия однозначности выразим столбец a n матрицы A через остальные функции:
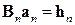 , – , –
| (3.22) |
или без индекса n
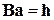 . .
| (3.23) |
Тогда, если система (3.23) невырожденная, т. е. det В ≠ 0, то она имеет единственное решение, которое можно найти по формулам Крамера или другим. Если система (3.23) вырожденная, то она имеет решение (притом неединственное) лишь при выполнении условий разрешимости, состоящих из равенства нулю соответствующих определителей [8].
Наличие экспериментально измеренных производных температур в правых частях уравнений системы (3.23) допускает их плохую обусловленность, которая может приводить к неустойчивости решения задачи нахождения вектора z.
Поскольку уравнения (3.20) и (3.23) подобны, в дальнейшем будет рассматриваться задача решения векторного уравнения
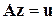 . .
| (3.24) |
относительно вектора z или
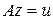
| (3.25) |
относительно функции z, где A – дифференциальный или интегральный оператор, что может соответствовать как постановке краевой задачи (3.5), 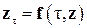 , так и обратной (3.23),
, так и обратной (3.23), 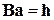 , с неустойчивым решением.
, с неустойчивым решением.
Основные понятия функционального анализа.
4.1. Метрические пространства.
Метрическим пространством называется пара (X, ρ), состоящая из некоторого множества (пространства) X элементов (точек) и расстояния, т. е. однозначной, неотрицательной, действительной функции ρ(x, y), определённой для любых x и y из X и подчинённой следующим трём аксиомам [9]:
1. ρ(x, y) = 0 тогда и только тогда, когда x = y,
2. ρ(x, y) = ρ(y, x) (аксиома симметрии),
3. ρ(x, z) = ρ(x, y) + ρ(y, z) (аксиома треугольника).
Метрическое пространство, т. е. пара (X, ρ) обозначается, как правило, одной буквой R = (X, ρ), а иногда, при отсутствии противоречий, буквой X.
Множество действительных чисел с расстоянием [9]
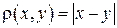 , ,
| (4.1) |
образует пространство R 1.
Множество упорядоченных групп из N действительных чисел x = (x1, …, x N) с расстоянием [9]

| (4.2) |
называется N -мерным арифметическим евклидовым пространством RN, с расстоянием [9]
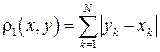
| (4.3) |
называется N -мерным метрическим пространством  , с расстоянием [9]
, с расстоянием [9]
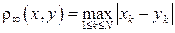
| (4.4) |
называется N -мерным метрическим пространством  .
.
Множество С [ a, b ] всех непрерывных действительных функций, определённых на отрезке [ a, b ], с расстоянием [9]
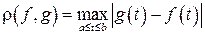
| (4.5) |
также образует метрическое пространство. Часто это пространство обозначается тем же символом С [ a, b ], что и само множество входящих в него функций.
Последовательность { zn } элементов метрического пространства R называется фундаментальной, если для любого ε > 0 найдётся такое натуральное число N (ε), что для любых 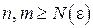 [8]
[8]
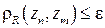 . .
| (4.6) |
Метрическое пространство R называется полным, если любая фундаментальная последовательность { zn } элементов этого пространства сходится к элементу из R.
4.2. Предельные точки. Замыкание.
Открытым шаром B (x 0, r) в метрическом пространстве R называется совокупность точек  , удовлетворяющих условию [9]
, удовлетворяющих условию [9]
 . .
| (4.7) |
Точка x 0 называется центром этого шара, а число r – его радиусом. Открытый шар радиуса ε с центом x 0 называется также ε-окрестностью точки x 0 и обозначается символом O ε(x 0).
Замкнутым шаром B [ x 0, r ] в метрическом пространстве R называется совокупность точек  , удовлетворяющих условию [9]
, удовлетворяющих условию [9]
 . .
| (4.8) |
Множество 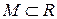 называется ограниченным, если оно содержится целиком в некотором шаре.
называется ограниченным, если оно содержится целиком в некотором шаре.
Точка  называется точкой прикосновения множества
называется точкой прикосновения множества  , если любая её окрестность содержит хотя бы одну точку из M. Совокупность всех точек прикосновения множества M обозначается [ M ] и называется замыканием этого множества. Переход от множества М к его замыканию [ M ] называется операцией замыкания.
, если любая её окрестность содержит хотя бы одну точку из M. Совокупность всех точек прикосновения множества M обозначается [ M ] и называется замыканием этого множества. Переход от множества М к его замыканию [ M ] называется операцией замыкания.
Теорема. Операция замыкания обладает следующими свойствами [9]:
1. 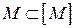 ;
;
2. 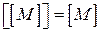 ;
;
3. если  , то
, то  ;
;
4. 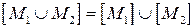 .
.
Точка  называется предельной точкой множества
называется предельной точкой множества  , если любая её окрестность содержит бесконечно много точек из M.
, если любая её окрестность содержит бесконечно много точек из M.
Точка 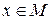 называется изолированной точкой этого множества, если в достаточно малой её окрестности O ε(x) нет точек из M, отличных от x.
называется изолированной точкой этого множества, если в достаточно малой её окрестности O ε(x) нет точек из M, отличных от x.
Отсюда можно заключить, что замыкание [ M ] состоит из точек трёх типов: изолированные точки множества M; предельные точки множества M, принадлежащие M; предельные точки множества M, не принадлежащие M [9].
4.3. Компактные множества. Компакт.
Множество 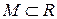 называется компактным на R (или в R), если из всякой его последовательности
называется компактным на R (или в R), если из всякой его последовательности  можно выделить подпоследовательность, сходящуюся к некоторому элементу из R [8].
можно выделить подпоследовательность, сходящуюся к некоторому элементу из R [8].
Необходимым и достаточным условием компактности множества 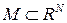 является его ограниченность.
является его ограниченность.
Достаточное условие компактности множества 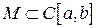 определяется следующей теоремой.
определяется следующей теоремой.
Теорема (Арцела). Если функции множества 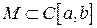 равномерно ограничены и равностепенно непрерывны, то из всякой последовательности
равномерно ограничены и равностепенно непрерывны, то из всякой последовательности 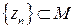 можно выделить подпоследовательность, равномерно сходящуюся к некоторой непрерывной на [ a, b ] функции [8].
можно выделить подпоследовательность, равномерно сходящуюся к некоторой непрерывной на [ a, b ] функции [8].
Если из всякой его последовательности  можно выделить подпоследовательность, сходящуюся к некоторому элементу из M, то множество M называется компактным в себе.
можно выделить подпоследовательность, сходящуюся к некоторому элементу из M, то множество M называется компактным в себе.
Каждое компактное в себе множество можно рассматривать как отдельное метрическое пространство (компакт).
Для того, чтобы компактное множество 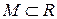 было компактом, необходимо и достаточно, чтобы оно было замкнуто в R.
было компактом, необходимо и достаточно, чтобы оно было замкнуто в R.
Всякий компакт M содержит конечное или счётное всюду плотное на M множество [8].
4.4. Функционал.
Отрезком метрического пространства R, соединяющим элементы z 1 и z 2, называется совокупность элементов z вида z = α z 1 + β z 2, где α, β – любые числа такие, что 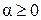 ,
, 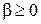 , α + β = 1 [8].
, α + β = 1 [8].
Множество 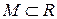 называется выпуклым, если с каждыми двумя элементами z 1, z 2 множества M ему принадлежат и все элементы отрезка, определяемого парой z 1, z 2.
называется выпуклым, если с каждыми двумя элементами z 1, z 2 множества M ему принадлежат и все элементы отрезка, определяемого парой z 1, z 2.
Числовая функция (т. е. функция, значениями которой являются числа), определённая на элементах множества M, называется функционалом, а множество M – его областью определения.
Функционал f (z) называется выпуклым, если он определён на выпуклом множестве M и для любых элементов z 1, z 2 из M и любых чисел α, β, таких, что 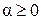 ,
, 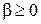 , α + β = 1 выполняется неравенство [8]
, α + β = 1 выполняется неравенство [8]
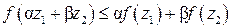 . .
| (4.9) |
Выпуклый функционал f (z) называется строго выпуклым, если для любых элементов z 1, z 2 из M (z 1 ≠ z 2) и любых чисел α, β таких, что 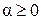 ,
, 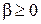 , α + β = 1 выполняется неравенство [8]
, α + β = 1 выполняется неравенство [8]
 . .
| (4.10) |
Функционал f (z), определённых на множестве 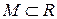 , называется непрерывным на M, если, для любых элемента z 0 из M и последовательности
, называется непрерывным на M, если, для любых элемента z 0 из M и последовательности 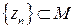 , сходящейся (в метрике R) к z 0, последовательность
, сходящейся (в метрике R) к z 0, последовательность 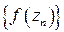 сходится к
сходится к 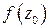 .
.
Функция f (x) одной вещественной переменной называется непрерывной справа в точке x 0, если [8]
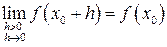 . .
| (4.11) |
Аналогично определяется непрерывность слева.
4.5. Линейные нормированные пространства.
Пространство R называется линейным, если для любых его двух элементов z 1, z 2 определён третий элемент  , который называется их суммой, и для любого
, который называется их суммой, и для любого  и любого числа β определён элемент
и любого числа β определён элемент 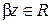 , который называется произведением элемента z на число β, причём, операции сложения и умножения на число удовлетворяют требованиям [8]:
, который называется произведением элемента z на число β, причём, операции сложения и умножения на число удовлетворяют требованиям [8]:
1. 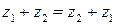 (коммутативность сложения);
(коммутативность сложения);
2.  (ассоциативность сложения);
(ассоциативность сложения);
3. существует элемент  (нуль пространства R) такой, что для любого
(нуль пространства R) такой, что для любого 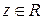 ,
, 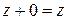 ;
;
4. для любого элемента  существует элемент – z такой, что
существует элемент – z такой, что  ;
;
5. для любых чисел α, β и произвольного  справедливо
справедливо 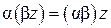 (ассоциативность умножения на число);
(ассоциативность умножения на число);
6. для любого  справедливо
справедливо 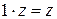 ;
;
7. для любых чисел α, β и произвольного  справедливо
справедливо 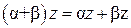 (дистрибутивность);
(дистрибутивность);
8. для любого числа β и произвольных  справедливо
справедливо 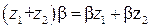 (дистрибутивность).
(дистрибутивность).
Нормой в линейном пространстве R называется функционал || z ||, определённый для любого  , принимающий лишь конечные вещественные значения и обладающий следующими свойствами [8]:
, принимающий лишь конечные вещественные значения и обладающий следующими свойствами [8]:
1.  для любого
для любого  ;
;
2. 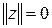 только для
только для 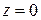 ;
;
3. для любых  справедливо
справедливо 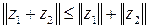 (неравенство треугольника);
(неравенство треугольника);
4. для любого числа β и произвольного 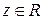 справедливо
справедливо
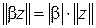 .
.
Если на пространстве R задана норма, то его можно сделать метрическим, положив  . Полученное пространство называется линейным нормированным пространством.
. Полученное пространство называется линейным нормированным пространством.
Примеры линейных нормированных пространств.
1. Пространство C [ a, b ] непрерывных на [ a, b ] функций z (x) [8]:
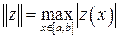 . .
| (4.12) |
2. Пространство L 1[ a, b ] функций z (x), интегрируемых с модулем
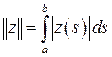 . .
| (4.13) |
3. Пространство L 2[ a, b ] функций z (x), интегрируемых с квадратом
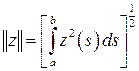 . .
| (4.14) |
Полное линейное нормированное пространство называется банаховым.
Линейное пространство R называется гильбертовым, если, во-первых, на нём задана вещественная числовая функция  ,
, 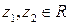 , называемая скалярным произведением, удовлетворяющая условиям:
, называемая скалярным произведением, удовлетворяющая условиям:
1. для любых 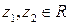 справедливо
справедливо  ;
;
2. для любых 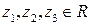 справедливо
справедливо  (аддитивность);
(аддитивность);
3. для любого произвольного вещественного числа β и любых 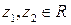 справедливо
справедливо 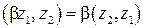 (однородность);
(однородность);
4. 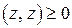 , причём,
, причём, 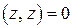 только для z = 0, –
только для z = 0, –
и, во-вторых, такое, что, если в R ввести метрику
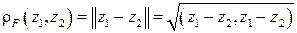 , ,
| (4.15) |
то пространство R с такой метрикой будет полным.
4.6. Проекция элемента на множество.
Пусть элемент y и множество Q принадлежат пространству U. Элемент q множества Q называется проекцией элемента y на множество Q, q = Py, если выполняется равенство
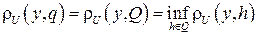 . .
| (4.16) |
Лекция IV